кону касательных напряжений. Нагрузки представляют собой энергетически эквивалентные силы, приписываемые к узлам (см. гл. 6). На рисунке изображены результаты численного эксперимента для вертикального смещения в нейтральном слое на свободном конце в зависимости от чпсла степеней свободы в конечно-элементной идеализации. Здесь в серии расчетов также используются CST- и LST-элементы. Решение, с которым проводится сравнение, берется из [9.15].

В этом случае видно, что использование CST-элементов не позволяет достичь приемлемой точности для числа степеней свободы, не превышающих 200. Результаты для LST-элементов значительно лучше, чем для CST-элементов, однако характеристики сходимости здесь значительно хуже, чем в предыдущем примере. Результаты экспериментов, приведенные в [9.3, 9.16], подтверждают сказанное. Другие численные решения показывают, что улучшение результатов, полученное при использовании треугольных элементов с квадратичным распределением деформаций в них, по сравнению с треугольными элементами с линейной деформацией не очень велико.

Приведенные результаты показывают, что при решении основных задач теории упругости о плоском напряженном состоянии предпочтительнее использовать треугольные элементы с линейной деформацией в них, а преи.мущества использования треугольных элементов более высокого порядка не столь очевидны. Каждое такое заключение должно быть смягчено рассмотрением стоимости построения коэффициентов жесткости элементов, размерности уравнений, а также возможностей решения глобальных уравнений и возможностей вычислительной машины. Заметим, что, хотя общая задача о плоском напряженном состоянии изучается адекватным образом, описанные ранее формулировки для плоского напряженного состояния не являются подходящим средство.м для анализа задач изгиба. Об этом речь пойдет в разд. 9.3.

9.2.5. Альтернативные вариационные принципы при построении треугольных элементов

Простота и достигаемая точность конечно-элементного представления, основанного на принципе минимума потенциальной энергии (базирующегося на перемещениях), в случае плоского напряженного состояния сдерживают развитие конечно-элементных представлений, опирающихся на альтернативные вариационные принципы. Как указывалось в гл. 7, принцип минимума дополнительной работы важен потому, что позволяет установить верхнюю границу для некоторых параметров решения. Однако его развитие и применение ограничиваются возникающими при построении элементов трудностями и пониманием того факта, что практическое

задание нагрузок и аппроксимация реальных геометрических характеристик могут привести к нарушению условий, обеспечивающих достижение верхней границы для решения.

Формулировки, основанные на принципе минимума дополнительной работы в задачах о плоском напряженном состоянии, включают задание функционала, содержащего вторые производные, если в качестве основной неизвестной выступает функция напряжений Эри Ф. Следовательно, требуется, чтобы Ф и ее первые производные были непрерывны при переходе от элемента к элементу. Эти вопросы интенсивно изучались в связи с задачами изгиба пластин, где нормальное смещение w должно удовлетворять дифференциальному уравнению того же вида, что и функция Ф. Выбор представлений для поля данного типа осуществляется в гл. 12. Сводка решений прикладных задач для плоского напряженного состояния приводится в [9.17].

В постановках задач о плоском напряженном состоянии с использованием понятия дополнительной энергии в качестве неизвестных в узлах могут приниматься также напряжения и другие силовые параметры. Некоторые авторы (см., например, [9.181) выбирали схемы этого типа для численной проверки верхней границы решения. При этом величины напряжений в треугольных элементах принимаются постоянными, а уравнения для элемента записываются с помощью матрицы жесткости, так что вся конструкция может быть рассчитана методом перемещений. Применение этой аналитической схемы наталкивается на трудности, обусловленные кинематической неустойчивостью (см. разд. 3.3).

В случае плоского напряженного состояния подход, основанный на дополнительной энергии, оказывается полезным также для задач неупругого анализа. В расчетах поведение материала определяется в форме зависимости деформаций от напряжений, т. е. с=[Е]~о. Поэтому для формулировок с потенциальной энергией требуется обращать это выражение, что может привести к трудностям при расчете задач с учетом временных зависимостей. При анализе предельных состояний [9.191 использовались преимущества подхода на базе дополнительной энергии.

Гибридный метод напряжений при построении элементов требует знания модифицированных форм функционала дополнительной энергии. Граничные свойства здесь уже неприменимы, однако в то же время можно гарантировать, что решение будет находиться между границами, определяемыми решениями, полученными с помощью обычных энергетических принципов. Более того, используя данный подход, удобно представить сингулярности в напряжениях. Указанные вопросы обсуждаются далее в разд. 9.3.3, где на примере прямоугольных элементов иллюстрируется гибридный метод напряжений для плоского напряженного состояния.

Наконец, заметим, что для плоского напряженного состояния формулировки на основе функционала энергии Рейсснера обладают теми же преимуществами и недостатками, что и формулировки на основе дополнительной работы. В [9.1] даются примеры применения подхода с использованием функционала энергии Рейсснера для треугольных элементов.

9.3. Прямоугольные элементы 9.3.1. Представления перемещений

Даже для прямоугольного элемента простейшего вида, имеющего узлы лишь в четырех угловых точках (рис. 9.12), можно сформулировать несколько альтернативных видов матриц жесткости. Число независимых параметров в представлении основного деформиро-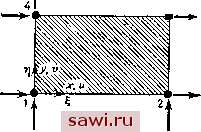

Рис. 9.12. Прямоугольный плоско-напряженный элемент. Типичные узловые силы и перемещения.

ванного состояния равно полному числу обобщенных координат, за исключением числа координат, отвечающих движению тела как твердого целого. В данном случае имеется восемь обобщенных координат (перемещения и и в четырех вершинах прямоугольника) и три моды движения тела как твердого целого. Поэтому полное число параметров, используемых для задания деформированного состояния, равно пяти. За вычетом трех параметров, предназначенных для удовлетворения условиям постоянства деформаций, имеется возможность выбора двух дополнительных параметров. В этом разделе рассмотрим два способа их задания.

Выписывая подробно первую матрицу жесткости для прямоугольного элемента, выберем поля перемещений и и v, которые изменяются линейно вдоль сторон элемента. Условие межэлементной непрерывности перемещений будет выполнено, если можно полностью представить такими элементами плоскую конструкцию или если данный элемент соединяется с CST-треугольными элемен-гамн. В разд. 8.4 было показано, что выбираемые поля перемеще-