НИИ ы= L N J {и} и и= L N J {v} задаются двухточечной интерполяционной функцией Лагранжа, где tx/x, у]=у/уз,

LNJ = L(l-i)(l-Tl)i?(l-ri)i?Tii(l-i)riJ. (9.13а)

{и}= 1 , 2 з 4 J. (9.13b)

{v\=lViV,V3V, \\ (9.13с)

Используя уравнения, связывающие перемещения и деформации, получим матрицу [D1 из (9.6) п. 9.2.1, коэффициенты которой равны

=L-(l-Tl)i(l-Tl)iTli-J.

(9.14)

= iL-(I-?)l-i:Si(l-?)J

где (и) и (v) в правой части соотношений (9.6) задаются с помощью (9.13Ь, с). Имея [D] и зная для конкретного типа материала (изотропного, ортотропного и т. д.) матрицу [Е], получим из выражения (9.7) матрицу жесткости в виде

[к] =

[DV[E][D] id А

Для изотропного материала окончательный вид матрицы жесткости в рассматриваемом случае приводится на рис. 9.13.

Интересно изучить основные свойства этой формулировки. Выбранное поле перемещений всюду (внутри элемента и при переходе через границы элементов) непрерывно. Что можно сказать об условиях равновесия? Подставляя выражения для и и v, получим следующие остаточные члены:

для уравнения равновесия в направлении оси х:

2(1 Л) .2,3 t- + a-a

ДЛЯ уравнения равновесия в направлении оси у:

2-(т4ь - = + - -Видно, что если перемещения задают равномерное расширение ( 1= 4, И2= з, Vt=V2, V3=Vi), выписанные выражения обращаются в нуль и имеет место равновесие. Тем самым невязки в выполнении условий равновесия пропорциональны сдвиговым деформациям. Сдвиговые напряжения меняются линейно внутри элемента. Нормальные напряжения постоянны вдоль направлений их действия, но меняются по линейному закону вдоль перпендикулярных направлений.

Представленный на рис. 9.12 элемент является базисным элементом в семействе лагранжевых плоско-напряженных прямоуголь-

7, =4

Тз =n -3(i)

Рис. 9.13. Матрица жесткости для прямоугольного элемента с линейным законом распределения граничных перемещений.

У, и

(и гу-)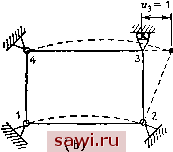

Рис. 9.14. Характер поведения прямоугольного элемента, основанного иа пятичлен-ном поле напряжений, (а) Напряжение и граничные усилия; (Ь) отклик на единичное перемещение Ug (смещение граничных точек изображено штриховой линией).

НЫХ элементов высокого порядка, названных так потому, что здесь поле перемещений строится с использованием интерполяционной формулы Лагранжа. Биквадратный элемент этого семейства приводится на рис. 8.7(b). Для построения множителей, входящих в функцию формы, используется квадратичная интерполяция. Операции по исключению внутренних и граничных степеней свободы, а также по преобразованию основного прямоугольного элемента в изопараметрический приводятся в разд. 8.7 и 8.8 и поэтому здесь не излагаются.

Второй детально описываемой в этом разделе формулировкой является наиболее ранний вариант построения матрицы жесткости для прямоугольного элемента [9.20]. Принципиально построение основано на следующих допускаемых полях напряжений:

Это поле напряжений иллюстрируется на рис. 9.14(a). Пластина имеет толщину /. Подставляя в дифференциальные уравнения рав