Литература

9.1. Dunham R S., Pister К S А Finite Element Application of the Hellinger- Reissner Variational Theorem.-Proc of the Second Conference on Matrix Methods in Structural Mechanics, AFFDL TR 68-150, p 471-487.

9.2 Pederson P. Some Properties of Linear Strain Triangles and Optimal Finite Element Models -Int. J Num. Meth Eng , 1973, 7, p 415-430

9 3. Brebbia С , Connor J J Fundamentals of Finite Element Techniques -London Butterworths Publishers, 1973.

9.4 Holand I. The Finite Element Method in Plane Stress Analysis, Chapter 2 of The Finite Element Method in Stress Analysis*, Holand and Bell (ed.).- Trondheim, Norway Tapir Press, 1969

9 5. Tocher J L , Hartz В J Higher-Order Finite Element for Plane Stress - Proc ASCE, J. Eng Mech Div , Aug 1967, 93, No. EM4, p. 149-174

9 6 Holand L., Bergan P G Discussion of Higher-Order Finite Element for Plane Stress)*.-Proc. ASCE, J Eng Mech Div., Apr 1968, 94, No EM2, p 698-702.

9 7. Walz J. E., Fulton R. E , Cyrus N. J , Eppink R T. Accuracy of Finite Element Approximations -NASA TN D-5728, Mar 1970 9.8. Taig I С , Kerr R. I. Some Problems in Discrete Element Representation of Aircraft Structures.- In Matrix Methods of Structural Analysis, В Fraeiis de Veubeke (ed.)-New York, N Y The MacMillan Co , 1964, p. 262~2Ы 9.9 Turcke D. J , McNeice G. M. Guidelines for Selecting Finite Element Grids

Based on an Optimization Theory -Int J Comp Struct , 1974, 4 9.10. McNeice G. M , Hunnisett S F Mixed-Displacement Finite-Element Analysis with Particular Application Using Plane Stress Triangles.-J Strain Analysis 1972, 7, No 4, p 243-252 9.11 Tong P Exact Solutions of Certain Problems by Finite Element Method.- AIAA J , 1969, 7, No 1, p 178-180 [Имеется перевод- Ракетная техн и космон - М. Мир, 1969, № 1.] 9.12. Oden J Т , Brauchli Н J On the Calculation of Consistent Stress Distribu-

Результаты показывают, что использование формулировок на базе линейных смещений на границе (межэлементно совместимых) приводит к довольно медленной сходимости к эталонному решению То же самое справедливо и для треугольных элементов (см. рис. 9.11). Напротив, использование формулировок с несовместимыми модами приводит к очень точным решениям в этой задаче Результаты для наименьшего числа степеней свободы 60 степеней свободы) получены при измельчении сетки лишь в направлении оси х, т. е. при одном элементе по толщине балки. Поэтому формулировки для плоско-напряженных задач общего вида можно использовать в представлении частных случаев изгиба, где обычно требуется выполнение гипотезы плоских сечений (плоские сечения до деформации остаются плоскими после нее). Для задач изгиба балок не часто требуется строить элементы, отличающиеся от простейшего нагибного элемента, однако в гл. 10 будет показано, что концепция несовместимых мод, являющаяся альтернативной в смысле интегрирования энергии деформации элемента на грубых сетках, весьма полезна при использовании трехмерных элементов теории упругости для анализа пластин и оболочек.

Задачи

9.1. Используя гибридный метод жесткости, постройте матрицу жесткости для треугольного элемента с постоянным значением напряжений (см. рис. 5.4).

9.2. Постройте смешанную матрицу сил и перемещений для плоско-напряженного треугольного элемента с постоянным значением напряжений в элементе, используя вариационный принцип Рейсснера. Полученную матрицу преобразуйте в матрицу жесткости элемента аналогично тому, как это делалось для булочного элемента из разд. 6 8

9.3. Проверьте правильность выражения для коэффициента кц матрицы жесткости прямоугольного элемента (см рис. 9.15) (F, в зависимости от Uj).

9.4. Постройте матрицу жесткости для кольцевого элемента, изображенного на рис Р9.4. Так как выполнены условия осевой симметрии, то tduldr, eQu/r. Выберите в качестве функции перемещений функцию u=l\-(r/r2i)]uj + + (/- -2 i)h2. где / 2-1=2-l-

9.5. Обсудите формулировку гибридного прямоугольного элемента на основе потенциальной энергии, используя для описания усилий на краях элемента функцию напряжений.

tions in Finite Element Approximations.-Int. J. Num. Metli Eng., 1471, 3, p. 317-322.

9.13 Hrennikoff A Precision of Finite Element Mettiod in Plane Stress.-Pub. Int. Assn. Bridge Struct Eng., 1969, 29-11, p. 125-137

9.14 TimoshenkoS.,Goodier J. N. Theory of Elasticity,2nd ed.-New York, N Y.: McGraw-Hill Book Co., p. 167-171, 1951 [Имеется перевод: Тимошенко С. П., Гудьер Дж Теория упругости.- М Наука, 1979, 560 с 1

9.15 Hooley R. F., Hibbert Р D. Bounding Plane Stress Solutions by Finite Elements.-Proc ASCE, J. Struct. Div., Feb. 1966, 92, No. ST. 1, p 39-48.

9.16 Cowper G R. Variational Procedures and Convergence of Finite Element Methods -In: Numerical and Computer Methods in Structural Mechanics, S.J Fenves, et al (eds.)-New York, N.Y.: Academic Press, 1973, p. 1 - 12.

9 17 Gallagher R. H., Dhalla A. K. Direct Flexibility-Finite Element Elastoplas-tic Analysis.-Proc. of First Internal Conf on Structural Mechanics m Reactor Technology, Berlin, Sept 1971, 6, Part M.

9.18 Fraeijs de Veubeke B. Upper and Lower Bounds in Matrix Structural Analysis.-In: Matrix Methods of Structural Analysis, B. Fraeijs de Veubeke (ed.).- New York, N Y.: The MacMillan Co., 1964, p. 166-201.

9.19. BelytschkoT., Hodge P. G. Plane Stress Limit Analysis by Finite Elements.- Proc ASCE, J. Eng. Mech. Div., Dec 1970, 96, No EM6, p. 931-44.6

9.20 Turner M. J., Glough R. W , Martin H. C, Topp L. J Stiffness and Deflection Analysis of Complex Structures.-J. Aero Sci., Sept 1956, 23, No. 23, 9, p 805-824

9.21. Wilson E. L., et al. Incompatible Displacement Models.-In: Numerical and Computer Method.* in Structural Mechanics, S. J. Fenves, et al. (eds.) -New York, N Y . Academic Press, 1973, p 43-57.

9 22. Plan T H. H. Derivation of Element Stiffness Matrices by Assumed Stress Distributions.-AIAA J., 1%4, 2, p 1333-1335 [Имеется перевод Ракетная техн и космон.- М . Мир, 1964.]

9 23 Plan Т. Н. Н., Tong Pin Basis of Finite Element Methods for Solid Continue - Int J. Num. Meth. Eng., 1969, 1, No. 1, p. 3-28.

9 24. Tong P., Plan T. H. H., Lasry S J. A Hybrid-Element Approach to Crack Problems in Plane Elasticity.-Int J. Num. Meth. Eng., 1973, 7, No 3, p 297-308.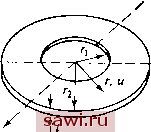

Рис. Р9.4.

9.6. Вычислите энергетически эквивалентные нагрузки для квадратичного закона распределения напряжений и сетки конечных элементов, указанной на рис. 9.10. Предположите, что в треугольных элементах деформации постоянны, а не меняются по линейному закону.

9.7. Постройте вектор начальных сил для треугольного элемента с линейно меняющейся деформацией в случае линейно меняющейся температуры в свободном от напряжения теле, т. е. Г=Л1Г1-(-Л2Г2--ЛзГз, где /V, и т. д.- функции формы линейного поля, а Гг и Гд - температуры в вершинах элемента.

9.8. Придумайте подходящее поле перемещений для построения матрицы жесткости секторного элемента, изображенного на рис. Р9.8 и постройте матрицу перехода от узловых смещений к деформациям [D .

(Типичные уз/1овые 4ir силы)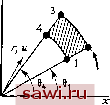

Рис. Р9.8.

9.9. (Численная задача.) Проведите конечно-элементный анализ квадратной пластины, изображенной на рис. Р9.9 (та же задача, что и на рис, 9.10), самостоя-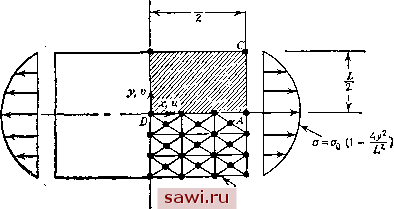

Сешка 3x3 {шитнак)

Рис. Р9.9.