Задачи

тельно выбирая тип элемента и сетки. Для сравнения решений как для перемещений, так и для напряжений см. работу: Cowper G. R., Lindberg G. М., Olson М. D. А Shallow Shell Finite Element of Triangular Shape.- Int. J. Solids and Structures, 1970, 6, p. 1133-1156.

Замечание. Необходимо строить сетку лишь в заштрихованном квадранте. Заметим, что и и V равны нулю в точке D, перемещения v равны нулю вдоль оси дг, а U - вдоль оси у; £=10 фунт/дюйм, Ц=0.3, /=1.

9.10. (Численная задача.) Проведите конечно-элементный анализ изображенной на рис. Р9.10 консольной балки прямоугольного сечения единичной толщины (та же задача, что и на рис. 9.11), самостоятельно выбирая тип элементов и сетку. Нагрузка Р распределена по параболическому закону в виде касательных напряжений, приложенных к прямоугольному поперечному сечению: Tjj =(2 9L)(1- -36I/VL2); £=10 фунт/дюйм2, ц=0.2, /=1.

I- Si--

Типичная mpej/го/гьная сетка внутри линии разбиения

Р 3

Рис. Р9.10 (сетка 3X9 изображена лишь в иллюстративных целях).

ТРЕХМЕРНЫЕ ЭЛЕМЕНТЫ: ОБЩИЙ СЛУЧАЙ

Сплошные, или трехмерные, элементы позволяют получить решение задач общей трехмерной теории упругости. Указанным задачам ранее уделялось относительно мало внимания при проектировании из-за трудности использования традиционных подходов к решению. Поэтому в этой области, за исключением простейших случаев, конечно-элементный анализ стал фактически неоспоримым средством отыскания решения. Имеются в виду такие задачи, как расчет массивных бетонных конструкций плотин, расчет напряжений в породах, решение задач механики для грунтов и скальных пород, возникающих при буровых работах, численное определение напряжений во фланцах и соединениях толстостенных труб.

Основные сплошные элементы представляют собой непосредственное обобщение на трехмерный случай плоских элементов. Изображенный на рис. 10.1(а) тетраэдральный элемент есть обобщение треугольного элемента на трехмерный случай, а шестигранный элемент (рис. 10.1 (Ь)) - трехмерный аналог плоского прямоугольного элемента. Хотя построены различные специальные и альтернативные виды трехмерных элементов (например, пятигранный или клинообразный элемент), на практике чаще используют тетраэдральный и шестигранный элементы. В этой главе рассматриваются только эти основные элементы.

Из-за проклятия размерности конечно-элементное представление для сплошного тела требует введения исключительно большого числа степеней свободы (рис. 10.2). Из рисунка видно, что если для получения решения заданной точности в одномерном случае требуется 10 степеней свободы, то в трехмерном случае - 3000. Поэтому решающими для использования метода в трехмерном случае являются вопросы экономичности. Необходимо добиться наибольшей эффективности выполнения (1) операций ввода и вывода данных, (2) процедур решения систем уравнений большой размерности,

(3) представления реальной конструкции ее конечно-элементной моделью.

Вопросы (1) и (2) лежат вне круга вопросов данной книги, читателю рекомендуется обратиться к литературе, цитируемой в конце данной главы. Требования (3) обусловливают применение очень сложных процедур представления геометрических характеристик. Поэтому концепция изопараметрического представления геометрии

г, и-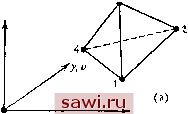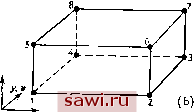

Рис. 10.1. Сплошные элементы: (а) элемент в виде правильного тетраэдра и оси координат; (Ь) элемент в виде правильного шестигранника и оси координат.

элемента, т. е. использование функций формы для описания границ элемента, приобретает особое значение для трехмерных элементов. Эти концепции развивались в разд. 8.8 и обсуждаются далее.

Существующие формулировки трехмерных элементов почти всецело основываются на предполагаемых полях перемещений и принципе минимума потенциальной энергии. Формулировкам на базе дополнительной энергии и смешанным формулировкам еще предстоит продемонстрировать свои преимущества для задач данного класса. Так, в задачах трехмерной упругости, если функционал дополнительной энергии выражен в терминах функции напряжений, то нужно преодолеть трудности, обусловленные операциями с функциями, которые непрерывны вместе с частью своих производных при переходе через границу элемента. Поэтому в данной главе рассматриваются лишь формулировки, основанные на предполагаемых перемещениях.