значения. Кромки пластинок искривляются, однако напряжения Оу О/ Для пластин на рис. 4.11, а при начальной погиби wj/=1,0 при достижении сжимающего напряжения критического значения, определяемого без учета погиби, погибь возрастает до wit S 2,5, а при wjt = 0,25 оиа увеличивается до wit \ ,25. У изогнутой пластинки (рнс. 4.11,6) при wjt 1 и wjt== 0,25 погибь достигает соответственно значений 1,6ш/< и 0,8и/Л

Искривление пластины приводит н возникновению в ией, помимо напряжений изгиба, напряжений растяжения или сжатия (так называемые мем-браиные> напряжения). Снижается жесткость властниы в направлении действия нагрузки.

При действии критических иа1пряже-иий и wlt= 1,0 напряжения превосходят средние расчетные значения в 2,5 и 1,4 раза соответственно для сжатой н изогнутой пластин. С учетом изгнб-ных и мембранных напряжений суммарные напряжения на поверхности пластин могут достигать 350 ... 170 % средних расчетных напряжений. Эти факторы особенно следует учитывать при оценке несущей способности балок ответственных иитеиснвио работающих кранов.

4.7. РАСЧЕТ

МЕТАЛЛОКОНСТРУКЦИЙ НА КРУЧЕНИЕ

В общем случае элементы коиструк-.ций, нагруженные внешним крутящим моментом Лкр, испытывают следующие виды напряжений:

касательные напряжения Хк, Хщ, действующие иа площадки, перпендикулярные к продольной оси элемента; иормвльиое напряжение Ощ, параллельное продольной оси элемента.

Крутящий момент прн действии внешних сил F

(4.45)

где / - расстояние от линии действия силы F до центра изгиба А, значения координат которого для некоторых сечений приведены в табл. 4.11 [18].

/И р = FI,

Свободное (иесгесиеияое) кручение стержней. При свободном (иестесиен-иом) кручении в стержне, иагружен-иом только крутящим моментом /Икр, возникают только касательные напряжения Тк.

Свободное кручение возникает: в угловых, тавровых и крестовых сечениях; в стержнях трубчатого круглого сечення; в призматических, коробча-тЫх стержнях прямоугольного сечения с размерами стенок и &2 и толщиной ti и <2, при обеспечеиии условия

= -т=- при квадратном сечении и а h

стеиках одинаковой толщины; в стержнях любого другого сечения, постоянного по длине стержня, и приложении крутящих моментов только к торцам, причем последние могут свободно перекашиваться в наиравлении продольной оси стержня, т. е. на торцах стержня отсутствуют препятствия к их де-плаиацин.

При свободном кручении в сечеиин возникают только касательные напряжения

х = /Инр/Г , (4.46)

где - момент сопротивления свободного кручения.

Для стержней открытого (незамкнутого) профиля, которые можно разбить на несколько п узких прямоугольников, осевой момент инерции при свободном кручеинн

где t{ и bi - толщина и ширина £-й полосы {см. рнс. 4.12, а); а - коэффициент формы сечения; для прокатных уголков а= 1,05; швеллеров а = = 1,10; двутавров а = 1,20; при уси-леКин профилей поперечными ребрами жесткости значения а возрастают; для двутавров а = 1,4-н1,6; тавров а = = 1,3-г1,6; сварных П-образиых сечений а= 1,5; прн соединении полок двутавра периодически установленными планками а 3,3; значения а для д )угнх профилей приведены в работе

Момент сопротивления

4.11. Координаты центра изгиба и секториальные характернстикн некоторых сеч(ений

Сечевне

Координаты а, ау центра нзгвба А

а, = О

СекторвальвыЯ момент инерции J

+

Эпюры секторнальвых коорднват о

ft , bd

h - расстояние от центра тяжести нижней полки до центра тяжести стенки швеллера

(4.48)

Примечание. J, У. - осевые моменты ииерцнн всего сечеиня относительно центральных осей X, Y; Jix, У{ -осевые моменты инерции элементов сечеиин i, 2, 3(i = 1, 2, 3) относительно центральшлх осей X, Y; Л , /llj,-осевые моменты инерции профилей I и II относительно центральной оси Y; Jja, /цш - секториальные моменты профилей I и II относительно собственных центров изгиба.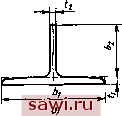

Рис. 4.12. Схемы поперечных сечений при расчете на крученне

Этот момент сопротивления соответствует точкам в срединной плоскости полос, составляющих профиль bi/2.

Для замкнутого профиля (рис. 4.12, б)

1 dsjt

(4.49)

где / - площадь, ограниченная осевой линией контура (обозначена на рис. 4.12, б штрнхпунктнрнон линией); s - протяженность средней линии; t - толщина стенки контура, при этом

Формулы для определения Jd и Wn для некоторых профилей металлоконструкций приведены в табл. 4.12.

Во внутренних углах прямоугольного сечения имеет место высокая концентрация напряжений.

Несвободное стесненное кручение стержней открытого профиля. Элементы стержней открытого профиля при действии поперечных сил начинают работать на изгиб. Эти силы обусловливают возникновение касательных напряжений Та и нормальных предельных напряжений Ощ.

В общем случае в каждом из сечений стержня действует крутящий мо-

4.12. Значения Jd и Ик для различных профилей металлоконструкций

Тип профиля

трубчатый (при Dopit >> 6)

Квадратный со стенками одинаковой толщины

Прямоугольный

Эскиз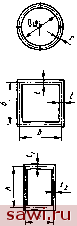

0.78ЛЗр/

t (ь - О

2 (6А)?

2/ (Ь - О?

2bhti

мент ЛГкр + Ма= М (здесь ЛГщ - изгибно-крутильный момент) и бимо-ментВщ.

Значения касательных напряжений -Сщ обычно не превосходят 5 ... 10 % Tr и при практических расчетах могут не учитываться.

Нормальные напряжении

Ощ = BJW,

(4.50)

где Wa - секториальный момент сопротивления; Wa = Ущ/ш (здесь со - секторнальная координата данной точки сечения; - секториальный момент инерции сечения).

Изгибно-крутильные геометрические характеристики двутавровых прокатных профилей приведены в табл. 4.13.

Изгибно-крутильные силовые факторы находят с учетом вида нагруження стержня, характера его опирания, а также коэффициента изгибно-кру-тнльной характеристики стержня:

GJd EJ

(4.51)

На рнс. 4.13, а-в показаны эпюры бимоментов Ва и крутящих моментов Л1кр для стержней, нагруженных внешним крутящим моментом М. На рис. 4.13, а торцы стержня имеют возможность свободной депланацни благодаря примыканию к тонкому листу. Депланацня торцов стержня на рис. 4.13, в исключена (примыкание к жесткой коробке). Стержень на рнс. 4.13, .S многопролетный, с возможностью депланацни в месте крепления на опорах (например, монорельс крана с решетчатым мостом).

Значения максимальных моментов 1181

Ml Ml

где n, /rtj - геометрические коэффициенты, принимаемые по данным табл. 4.14 в зависимости от безразмерного параметра Ы; I - пролет стержня.

Угол поворота среднего сечення стержня

М ( kl \

р = -2Ршг(-2---т;-

(4.52)

4.13. Значения изгибно-крутильных геометрических характеристик двутавровых прокатных профилей

4.14. Значении геометрических коэффициентов in и п в зависимости от параметра Ы

Стесиениое кручение стержней замкнутого профиля. Нормальные напряжения Ощ при стесненном кручении стержни (рис. 4.14, а, б) вызывают де-

иг J

а) S)

Рнс. 4.13. Эпюры внешних крутящих моментов М, бимоментов Вщ н крутящих моментов Л1кр при различных закреплениях концов стержня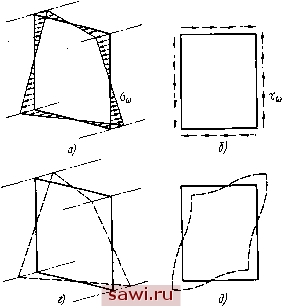

Рис. 4.14. Напряжения и деформации при кручении балкн прямоугольного

сечення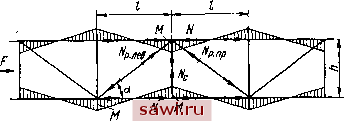

Рис. 4.15. Схема к расчету дополнительных усилий и моментов в элементах центрально-нагруженной решетчатой конструкции

плаиацию сечения; касательные напряжения при стесненном кручении (рнс. 4.14, в, г) - искажение контура сечения в результате изгиба стенок и поясов и возникновения в них напряжений изгиба; касательные напряжения прн своб(дном кручении (рнс. 4.14, д, ё) - поворот сечення.

Если шаг расстановки диафрагм составляет 1,5 ... 2,5 высоты сечення балкн, то напряжения относительно невелики. Однако увеличение шага расстановки диафрагм следует учитывать прн расчете несущей способности конструкции, в особенности прн применении относительно податливых рамных диафрагм [124].

В большинстве случаев, когда внешние крутящие моменты, действующие на элемент, относительно невелики, влиянием напряжений стесненного кручения можно пренебречь. Их следует учитывать только прн расчете элементов, интенсивно работающих на кручение, например, пролетных балок мостовых кранов с расположением рельса над стенкой нлн с консольной грузовой тележкой. В этих случаях рекомендуется использовать методику В. П. Хлебородова (РТМ 24.090-83).

4.8, ОСОБЕННОСТИ РАСЧЕТА ФЕРМЕННЫХ КОНСТРУКЦИЙ

Определение усилий и изгибающих моментов в стержнях ферменных конструкций наиболее целесообразно выполнять с помощью ЭВМ, что позволяет рассчитать любую ферму.

Предварительные расчеты обычно выполняют с помощью аналитических и графических методов, представляя

узлы фермы шарнирными. При этом в необходимых случаях дополнительно учитывают фактически действующие в узлах моменты.

Цевтральио-иагружеииые решетчатые стойки или сжато-растянутые грани решетчатых конструкций. Вследствие деформаций поясов раскосы также участвуют в передаче продольной силы Р. Знак деформации элементов (раскосов и поясов решетки) соответствует знаку деформации поясов.

Напряжение в элементах решетки

ор од cos а,

где оц - напряжение в поясе; а - угол между элементами решетки и поясом.

Более точно силы, действующие в раскосах (рнс. 4.15), могут быть определены по формуле

одлр cos а

1 + 42-3in а + cos а

(4.53)

где лр - площадь раскоса; А с- площадь сгонки; J - момент ннерцнн пояса относительно оси, перпендикулярной к плоскости конструкции; h - высота фермы. Силы, действующие на стойку,

Лс = (iVp. лев +/Vp. пр) sin а.

Следует также учитывать (за исключением расчетов на устойчивость) дополнительные изгибающие моменты в поясах

М = ±0,25iVc/.

Дополнительные изгибающие момев-ты в поясах моста при изгибе. Прн от-

B:/B