Используя формулу (53у, найдем мгновенное передаточное отношение t от звена / к звену 3 (прямой кулисный механизм):

i = = 1 4- -2Xcosip to, I - X cos ф

(55)

Без учета угла \ относительного поворота элементов МСХ в процессе заклинивания момент заклинивания будет определяться точкой /, а момент расклинивания точкой 1 .

При этом углы

Углы

9 = -- + arcsin(sin-£-); Ф = -arcsinfXsin-v

(56)

Угол сдвига Дф двух соседних пар роликов

Аф - ф - ф =

--2arcsinf;isln-v

(57)

Итак, величина фазового угла Аф зависит от величины т и X.

Среднее передаточное отношение прямого кулисного механизма можно представить как отношение углов поворота ведущего звена / и сепаратора 3 на участке /-/ (рис. 14, б):

i = Ф -Ф Аф 1 Р Р - р

а с учетом формул (56) и (57)

ii=,l-arcsin(;isin-). (58)

Если число пар роликов относительно велико (например т = = 12), то угол - принимает небольшие значения, и тогда можно принять

ti 1 - Я,.

Рассмотривая обратный кулисный механизм из треугольника ОСА (см. рис. 14, б), имеем

sin (у-Р) / , sin р - -

Y = р -Ь arcsin {X sin р).

Заклинивание роликов 5 определяется положением 2, а расклинивание-положением 2 . Для данных положений углы и р определяются по формулам (56), а значения у viy - по формуле (59):

= arcsin (sin-);

v = + arcsin(Xsin-).

Среднее передаточное отношение г- у -у ~

+ - arcsin I X, sin - I

или приближенно 1

Полное среднее передаточное отношение вариатора

I = =

arcsin (А- sin- I я \ т J

1-4--- arcsin я

или приближенно

in Я, sin

(60)

(61)

Из формул (60) и (61) следует, что когда эксцентриситет сепаратора равен нулю (Х = 0), передаточное отношение i = I, т. е. ведомый вал вращается как единое целое с ведущим. При всех других значениях 1, больших нуля, t < 1 и, следовательно, без дифференциального механизма передача является ускорительной.

ВАРИАТОР С КАЧАЮЩЕЙСЯ ШАЙБОЙ

На рис. 15, а показана кинематическая схема вариатора (см. гл. 1, рис. 26), где преобразующий механизм представляет собой пространственный рычажный механизм с качающейся шайбой. Ведущий вал / приводит в движение качающуюся шайбу 2, перемещающую в осевом направлении подпружиненные плунжеры 5, несущие на конце ролики 4, которые перекатываясь по наклонному пазу ротора 5, приводят ротор, соединенный неподвижно с ведомым валом, во вращательное движение. Благодаря наличию МСХ вращение передается только в одном направлении.

Если обозначить: R - расстояние осей плунжеров от оси ведомого вала; v -~ У - наклона шайбы; ф - угол поворота шайбы, то согласно схеме движения плунжеров и наклонной шайбы

(рис. 15, б), приняв за начало отсчета угла ф крайнее правое положение плунжера, можно определить его осевое перемещение у. При повороте шайбы на угол ф конец плунжера, соприкасающийся с шайбой, переместится в осевом направлении на

yDE-AB R tgv-i? tgYcosф = tg у (1 - cos ф), (62)

и, следовательно, осевая скорость плунжера

V = R igy (Hi sin ф,

где Ml - угловая скорость ведущего вала.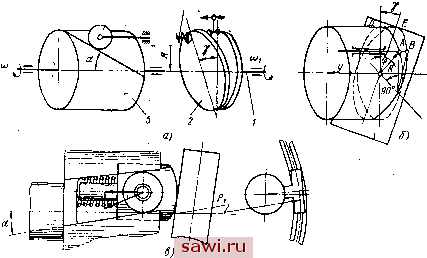

Рис. 15

Зная осевую скорость плунжеров v, угол а наклона паза ротора, расстояние средней линии ролика от оси ротора (см. рис. 15, в), найдем угловую скорость ведомого вала

со =JiЖi= tgYtgasinфCDl (63)

и передаточное число вариатора

W tg Y tg а sin ф (64)

Если число плунжеров и соответственно число МСХ равно k, то угловая скорость со ведомого вала и передаточное число \ будут изменяться периодически за каждый угол поворота шайбы При этом угол ф изменяется в диапазоне от начала заклинивания МСХ ДО момента его расклинивания.

Из уравнений (63) и (64) можно заключить, что данная конструкция вариатора позволяет изменять неравномерность движения ведомого вала посредством изменения угла а и радиуса R

в функции ула ф. Первое можно достигнуть изменением формы паза ротора, а второе за счет формы рабочей поверхности шайбы и опорной поверхности толкателя [72], [73]. В более общем случае передаточное отношение

tgT (Ф) tg [а (ф)] sin ф

(65)

При регулировании угловой скорости ведомого вала вариатора теоретически минимальная величина (0 = 0 при у = 0. В действительности, как показали опыты с другими системами импульсных вариаторов, они теряют работоспособность (периодически останавливаются) при больших конечных значениях i, когда со >0.

Реальная минимальная угловая скорость ведомого вала вариатора определится из равенства (63):

min = - itg Yшlntgasin(ф),

(66)

где Y j, - минимальный угол наклонной шайбы, при котором вариатор нормально функционирует (движение при постоянной неравномерности).

Величина этого угла определяется экспериментально. На основании выражения (71) кинематический диапазон регулирования

(67)

2 ) Цтах . Ушах

<ш1п 7mln

Как следует из уравнения (63), максимальная угловая скорость ведомого вала при проектировании вариаторов может быть увеличена за счет увеличения отношения углов у и а, угловой скорости вала электродвигателя со. Однако все эти величины огра-ничены. Отношение < 1 практически остается постоянным,

имея тенденции к небольшому увеличению с увеличением радиальных размеров ротора. Величины углов y иа не должны превышать соответственно предельных углов передачи в механизме с наклонной шайбой и в пространственном кулачковом механизме с ведущим толкателем. Все это указывает на то, что рассматриваемые вариаторы могут работать в диапазоне малых частот вращения ведомого вала (п = 0-90 об/мин).

Угловая скорость ограничивается условием непрерывности контакта толкателя с шайбой. При больших значениях coi и угла y возможны отрывы толкателей от шайбы, что неизбежно приведет либо к значительному сокращению импульса, передаваемого ведомому валу со сторсшы ведущей части механизма вариатора, либо к пропуску импульсов отдельными толкателями. Как в первом, так и во втором случае резкр возрастут динамические усилия и возможно соударение элементов механизма.

Глава 4

РЕГУЛИРУЮЩИЕ МЕХАНИЗМЫ ЗУБЧА ТО-РЫЧАЖНЫХ ВАРИАТОРОВ

в вариаторах общемашиностроительного назначения регулирующие механизмы конструктивно увязываются с механизмом главного движения. Они разнообразны по принципу действия, конструктивному выполнению и воспроизводят различные законы изменения передаточного отношения привода в зависимости от перемещения их ведущего звена.

Регулирующие механизмы, во-первых, должны обеспечить плавное изменение передаточного отношения и, во вторых, надежно его фиксировать. Второе условие особо важно выполнить для импульсных вариаторов, у которых импульсивность в механизме главного движения может вызвать самопроизвольное перемещение регулирующего звена и, следовательно, разрегулировку привода на заданное передаточное отношение.

Фиксирование регулирующего звена достигается за счет применения самотормозящихся передаточных механизмов и фиксирующих устройств, не нарушающих бесступенчатость регулирования или их комбинацию. В силу простоты устройства и способности фиксации у большинства вариаторов применена самотормозящаяся винтовая пара, а в тех случаях, когда самоторможение пары недостаточно, дополнительно устанавливают подтормаживающие устройства или контргайки.

Особое внимание следует обратить на жесткость всей системы регулирующего механизма. Наличие нежестких звеньев неизбежно приведет к изменению амплитуды колебания ведущих звеньев МСХ импульсных вариаторов, при этом появляется кажущееся скольжение и изменение жесткости характеристики вариатора

С целью удобства управления вариатором, особенно в тех случаях, когда вариатор расположен на значительном расстоянии, применяют дистанционное ручное управление механического (цепные передачи, карданные, гибкие валы и др.), гидравлического (см. гл. 2, рис. 8) и электрического (см. гл. 2, рис. 16) действия.

При разработке передач с бесступенчатым автоматическим регулированием важно знать не только усилия, действующие на

звенья регулирующего механизма, и по ним рассчитать элементы на прочность и особенно на жесткость, но и его кинематические свойства и прежде всего законы изменения передаточного отношения вариатора в функции координаты перемещения регулирующего звена, которой чаще всего является угол поворота а ведущего звена регулирующего механизма.

Плавность регулирования и быстродействие вариатора можно характеризовать изменением передаточного отношения в единицу времени. Условимся назцвать скорость, изменения среднего передаточного отношения чувствительностью регулирования, которую можно определить по формуле di

где i - передаточное отношение передачи; t - время.

В дальнейшем рассматриваются регулирующие механизмы, у которых регулирование осуществляется поворотом звена, непосредственно воздействующего на изменение эксцентриситета пазового диска.

Дифференциал времени

где сор - угловая скорость ведущего звена регулирующего меха-

низма.

Подставляя значение дифференциала времени в формулу (1), получим

(Op di da

Объем книги не позволяет рассмотреть все многообразие регулирующих механизмов импульсных вариаторов. Поэтому ниже рассмотрены только регулирующие механизмы наиболее современных зубчато-рычажных вариаторов, которые нашли применение в приводах с автоматическим управлением.

Методический подход при определении закономерности изменения передаточного отношения в процессе регулирования и оценка плавности изменения частоты вращения ведущего вала, изложенные в этой главе, могут быть перенесены и на регулирующие механизмы других систем импульсных вариаторов.

У зубчато-рычажных импульсных вариаторов посредством регулирующих механизмов плавно изменяется длина кривошипа преобразующего механизма, причем движение регулирующие механизмы получают непосредственно от их ведущего звена или от механизма главного движения путем периодического подключения к последнему. У первой разновидности регулирующих механизмов передаточное отношение вариатора изменяется в зависимости от угла поворота регу;ирующего звена. Они дают возможность вести регулировку во время движения и с выключенным