Дифференциальное уравнение движения за период от начала заклинивания МСХ до периода его расклинивания, когда ведомые звенья преобразующего механизма и МСХ движутся совместно, имеет вид

{M~M,)dц>Jiod(o + dJ. (5)

Подставляя в это выражение значения Мд, и /, определенные из формул (Х), (3) и (4), получим дифференциальное уравнение Движедия за малый угол поворота звена приведения Дф;:

du) a,--f bia-cico*- ф tg at

dt ~

Ф + Ф tg pi

где

ai = Mmax - A(Oc.~ B(dl - Mci + tg 0,1

Построение касательной в любой точке плоскости фОю (рис. 3, в) на основании уравнения (6) дает возможность приближенно интегрировать уравнение (5). Для этого разбиваем графики Л1 е = Мс (ф) и J - J (ф) на одинаковое число элементов и в пределах каждого элемента криволинейные участки графиков заменяем прямолинейными. Затем для каждого элемента находим значение величин а, Ь, d и углов аир, после чего, определив по формуле (6) угловые коэффициенты, проводим касательные к интегральной кривой.

Начнем отсчет угла поворота кривошипа с момента заклинивания МСХ. Так как заклиниванию предшествовал свободный ход механизма (см. рис. 1), то начальные условия можно записать так:

Фо = 0; (Оо = сй ,ах.

С целью повышения точности построения интегральной кривой пользуемся методом добавочного полушага.

Нанеся на график (см. рис. 3, в) начальную точку k {О, (оах), строим соседнюю точку интегральной кривой. Для этого из уравнения (6) определяем направление касательной в точке k и проводим эту касательную (линия п-п, рис. 3, в) до пересечения в точке (фв >s) с вертикалью, восстановленной из середины первого участка. В точке s аналогично, как и в точке k, находим направление касательной со, которая на рис. 3, в показана линией т.-т. Далее из точки k проводим линию параллельно касательной т-т до пересечения с правой вертикалью первого участка в искомой точке g (фg, (Og); Затем таким же способом, принимая точку g

за начальную, находим для следующего участка точку г (ц> ©,) и т. д. Соединив плавной кривой точки k, g, г я т. д., получим график (О = (О (ф).

В зависимости от вида преобразующего механизма в каждом конкретном случае можно определить передаточное отношение i между кривошипом и колеблющимся звеном как функцию угла ф.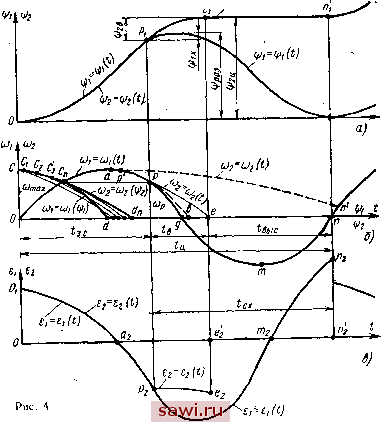

т. е. i = i (ф). Закон изменения угловой скорости (Oi ведомого звена преобразующего механизма:

1 i (ф) 1-

Известными методами на основании последнего выражения строим зависимость coi = coi {t) (кривая Oab на рис. 4, б) и ©i = = 1 (i) (кривая cd). Последнюю кривую строим только для периода уменьшения ©i. Это необходимо при определении момента расклинивания мех.анизма, так как точка, определяющая момент расклинивания, как ранее указывалось, является общей

точкой кривых (x)i = (i>i{\pi) И (Og = (Og (if2)- Зависимость tt 2 =

= (O2 (ifa) определяется в результате решения дифференциального уравнения движения ведомой системы в период ее выбега после расклинивания МСХ, которое имеет вид

- Мс =-- --- dJ + /(02 dm.

Знак минус указывает на то, что приведенный момент Мс действует в сторону, обратную вращению звена приведения. Здесь за звено приведения принято ведомое звено МСХ.

Начальная точка интегральной кривой уравнения (7) неизвестна, она является и искомой точкой, соответствующей моменту расклинивания. Дйя ее нахождения строим семейство интегральных кривых (О2 = (О2 {2) на основании уравнения (7), учитывая при этом, что расклинивание может произойти при угловой скорости ведущего и ведомого звеньев механизма меньшей, чем (оах. Поэтому в качестве начальных точек при построении этих кривых последовательно выбираем точки Cj, с, Сд, с на кривой со = ~ 1 (i) передвигаясь вправо от точки с, как показано на рис. 4, б. Та точка на кривой cd, которая наиболее близко расположена к точке с и начиная от которой кривая (О2 = (О2 {р) проходит выше кривой со = со (if), соответствует моменту расклинивания. На рис. 4, б такой точкой является точка с . Кривая (О2 = 2 (if 2) из семейства кривых, для которой эта точка является начальной, определяет закон движения ведомой системы после момента расклинивания МСХ.

Проведем из точки с линию, параллельную оси абсцисс, до пересечения с кривой со = со (t) в точке р. Абсцисса последней точки, очевидно, равна времени периода заклиненного состояния МСХ 4 , а ордината - угловой скорости сОр ведущего и ведомого звеньев МСХ в момент расклинивания.

Определим по кривой со2 = со 2 (ypi) (кривая c (i ) методом исключения угла гр график СО2 = СО2 (t) и построим его из точки р (кривая ре), в результате чего найдем время выбега ведомой системы привода.

Изменение угловой скорости со после момента расклинивания (кривая pgmn) в функции времени определяетбя аналогично, как и для периода заклиненного состояния, с той лишь разницей, что в уравнении (5) вместо момента сил сопротивления М и момента инерции J всей системы машинного агрегата будут фигурировать момент сил сопротивления Мс и момент инерции J ведущей системы. Точка п пересечения оси абсцисс и кривой coi = coj (t) определит момент заклинивания и позволит найти (рис. 4) время е. X свободного хода, а также время выс выстоя ведомой системы в период свободного движения МСХ. После точки п цикл движения будет повторяться.

Если период выбега ведомой системы окажется настолько продолжительным, что кривая со2 = со2 (О Для этого периода 134

(пунктирная линия рп) пересечет кривую со = со (t) выще оси абсцисс, то следующий цикл движения начнется при угловой скорости coj, большей нуля, т. е. при угловой скорости, отличной от начальной угловой скорости предыдущего цикла, что, как известно, не должно иметь места при установившемся движении. В этом случае следует производить построение диаграмм со = = со 1 (i) и со 2 = со 2 (О до тех пор, пока величины скоростей для одноименных фаз движения не начнут повторяться. Обычно для этого, как показал анализ некоторых импульсных вариаторов, достаточно построений для двух-трех циклов.

Если расклинивания механизма в период убывания со не произойдет (третий случай движения ведомой системы), задача значительно упрощается, так как моменты заклинивания и расклинивания вполне определены, а именно: заклинивание произойдет в начале прямого хода ведомого звена преобразующего механизма, а расклинивание - в начале обратного хода.

В этом случае закон движения в период прямого хода, т. е. в период заклиненного состояния МСХ, а равно и закон движения ведомого звена преобразующего механизма в период обратного хода определяются теми же способами, что и в ранее рассмотренных случаях. Ведомый вал вариатора в течение всего обратного хода для этого случая остается неподвижным.

По графикам со =.©1 (t) и со2 = сог (t) путем интегрирования и дифференцирования строим соответственно диаграммы ifj = = ifi (t) и 1JJ2 = 12 (О углов поворота ведомого звена преобразующего механизма и ведомого звена МСХ в функции времени (см. рис. 4j, а) и диаграммы = (t) и 82 = 82 (О углового ускорения этих звеньев (см. рис. 4, в).

Изменение угла поворота if = if (t) за период полного цикла движения МСХ показано графиком Opitii (см. рис. 4, а), а изменение угла поворота if 2 = if 2 (О ~ графиком Opieitii.

Если обозначить: if 2ц - угол поворота ведомого звена МСХ за один цикл движения вариатора; ifpgg - угол размаха ведомого звена преобразующего механизма; if 2в - угол поворота ведомого звена МСХ за период выбега ведомой системы; if - Угол поворота ведомого звена преобразующего механизма за время холостого движения в период прямого хода, то на основании графиков, показанных на рис. 4, а, имеем if2ц = ifpaa + 2в - ix-

Нетрудно сообразить, что величина угла if2 увеличивается с увеличением угловой скорости со кривошипа преобразующего механизма и приведенного момента инерции J ведомой системы, а также с уменьшением момента Мс сил сопротивления ведомой системы в силу увеличения угла ifas- Здесь необходимо заметить, что при этом также возрастет величина угла if j. но в меньшей мере, чем угол if2B.

Зависимость = ei ( за цикл показана в виде графика OiuPimitii (см. рис. 4, в), а вависимость 82 = 62 (t) за цикл - в виде графика OxaPihlnk.

Динамика простейших вариаторов при щ - const. Исследование импульсных вариаторов упрощается, если вращение ведущего звена преобразующего механизма можно считать происходящим с постоянной угловой скоростью, что может иметь место при сравнительно малых усилиях сопротивления и небольших массах звеньев ведущей и ведомой систем. К таким случаям относятся импульсные вариаторы, применяющиеся в приводах подач питающих устройств, дозаторов и др. Рассмотрим наиболее распро-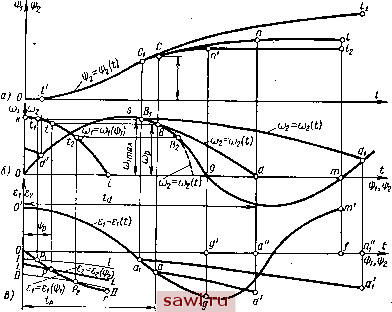

Рис. 5

страненную схему указанных приводов, когда ведомая. система имеет постоянный приведенный момент инерции J .

Определим обычным методом кинематики механизмов периодическую зависимость с периодом изменения угловой

скорости coj ведомого звена преобразующего механизма от времени t. Эта зависимость показана на рис. 5, б в виде графика OBgm. В период повышения угловой скорости (о на участке ОВ МСХ включен, при этом ведомые звенья преобразующего механизма и МСХ вращаются совместно так, что выполняется условие со = = ©2 и = eg. Это условие сохраняется вплоть до момента расклинивания МСХ в период спада угловой скорости и наступления периода выбега ведомой части вариатора.

Если произойдет расклинивание МСХ в период спада угловой скорости (Oi, то после приведения сил и масс к звену приведения -

ведомому элементу МСХ уравнение движения ведомой системы в период выбега будет иметь вид

Мс = /ег.

При заданном законе изменения момента сил сопротивления ведомой части Мс = Мс {i) из последнего уравнения определяем

Если ведомая система имеет 1, 2, 3, п вращающихся звеньев, то величина приведенного момента инерции

J =

где Ji - момент инерции i-ro звена относительно оси вращения; и, - угловая скорость 1-го звена.

Для того чтобы определить момент расклинивания МСХ, построим в левой части на рис. 5, б график ki изменения угловой скорости ©1. Затем в результате дифференцирования на рис. 5, в построим график Or изменения углового ускорения в период спада угловой скорости © в зависимости от угла rpi. Кроме того, .на рис. 5, в нанесем кривую LL изменения углового ускорения 82 в функции угла г)2 ДЛя этого же периода соответственно уравнению (8).

Угол поворота ведущего и ведомого звеньев МСХ соответствующий моменту расклинивания, определяется точкой р пересечения кривых 81 = 81 и 82 = 82 hPz), так как в этот момент* 8 = 82. Проведя из точки р вертикальную прямую, получим при еепересечении с кривой © = © {i) точку t, ордината которой является угловой скоростью Юр ведомого и ведущего звеньев МСХ-Б момент расклинивания. Далее проводим из точки t линию,-параллельную оси абсцисс до пересечения в точке b с кривой (0 = (0. (t). Абсцисса точки В определяет время tp, соответствующее расклиниванию МСХ. Следует оговориться, что величину (Ар можно определить без построения кривой © = © из плана скоростей преобразующего механизма для положения, соответствующего углу г)р, или непосредственно из уравнения со = ©1 если оно задано аналитически. При этом график

= строится на основании планов ускорений преобразу-

ющего механизма или по уравнению 8 = 81 если последнее выражено аналитически.

Начиная с точки В, закон изменения угловой скорости ©2 определяется в результате интегрирования уравнения (8):

©2 =3

©г