Получив зависимость (о = (2) метрдом исключения угла, можно найти зависимость co = coj (0- Предположим, что кривая

= 2 (О, проведенная из точки В, пересечет ось абсцисс в точке d, соответствующей моменту времени tj, при котором ведомый вал вариатора остановится, после чего на участке - будет наблюдаться выстой этого звена. Время 4 периода выбега определится из выражения

(10)

Для построения графиков углор поворота ведомого вала (кривая СП на рис. 5, а) интегрируем на участке tp-ta зависимость >2 = ©2 (О- На последнем участке цикла п1 угол г)2, очевидно, остается постоянным, так как ведомый вал имеет выстой. Таким образом, за один цикл движения в этом случае закон изменения угла поворота ведомого звена яг = 2 {t) будет изображен кривой Ocnl (см. рис. 5, а), закон изменения угловой скорости ©2 = = 2 (t) - в виде кривой OBdm (см. рис. 5, б) и закон изменения углового ускорения 82 = 82(0 -в виде кривой 0aaa f (см. рис. 5, в).

Нетрудно заметить, что с уменьщением нагрузки, т.е. с уменьшением приведенного момента сопротивления Мс и увеличением приведенного момента инерции J и максимальной скорости >imax ведомого звсна преобразующего механизма, в период прямого хода при одном и том же преобразующем механизме период выбега ведомой части увеличивается и, следовательно, увеличивается угол поворота ведомого звена г)2ц за цикл движения ведомого вала вариатора.. При этом закон (л = (О2 (t) в данный период будет представлен более пологой кривой. Наоборот, с увеличением Мс и уменьшением J я соах период выбега уменьшается, а также уменьшается угол \р2а. за цикл движения; кривая (О2 = = 2 (i) для этого периода становится более крутой.

Для иллюстрации сказанного на рис. 5, в кроме кривой LL, углового ускорения 82 = 82 ( нанесены еще кривые /-/ и - графики этого ускорения. Кривая /-/ соответствует меньшему, чем в ранее рассмотренном случае, моменту сил сопротивления Щ и большему приведенному моменту инерции J ведомой части, а кривая II-II - большему моменту сил сопротивления и меньшему моменту инерции. Величины Мс и J при построении графика /-/ выбраны с таким расчетом, чтобы движение ведомого звена соответствовало второму случаю движения.

Соответственно кривой /-/ построены графики за один цикл tcji углов поворота xfa = 2 (О dBid угловой скорости ©2 = = ©2(0 и Оаа! - углового ускорения 62 = 82(0 ведомого звена. Большее значение Mi и меньшее значение J при определе-

НИИ кривой - выбраны такими, что кривая изменения ©2 = = ©2 (О, определенная по режиму выбега, идет круче, чем кривая = ©1 (О, и, следовательно, выбега в период спада угловой скорости ©1 не будет, что, как указывалось выше, соответствует третьему случаю движения. При этом графики за цикл будут: Onh - углов поворота ifa = 2 (0; ОВт - угловой скорости (02 = 2 (0; Oggf - углового ускорения 82 = 82 (О-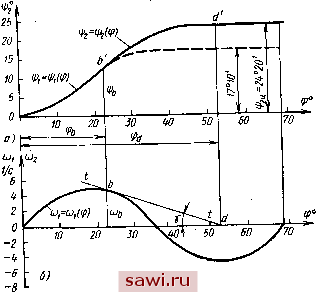

Рис. 6

При Mi = const уравнение (8) можно представить в следующем виде:

© =

dip J

Проинтегрировав это уравнение, получим

(02 = -Ф + С,

следовательно, угловая скорость ©2 в период выбега ведомой системы изменяется по линейной зависимости. Поэтому для определения момента расклинивания необходимо построить график (0 = (Oi (ф) и к нему провести касательную tl (рис. 6, б) под углом

а = arctg

Точка касания b определит* момент расклинивания и значение угловой скорости ©в и угла поворота фв в этот момент.

Постоянная интегрирования

С = (О, +

И, следовательно, закон изменения угловой скорости ведомого звена в период выбега имеет вид

Для построения графика угла поворота ведомого звена представим уравнение (12) в следующем виде:

= *--7Г(ф-фб)-

Интегрируя его, получим

2 = + (Ф - ф,) - 2 (ф -

(13)

Выражение (13) представляет уравнение параболы в коорди- натнои системе р, ф. По этому уравнению на участке ф.-т. построена кривая изменения угла поворота >2 = ijj (ф).

Пример. Найти угол поворота за один цикл ведомого мла импульсного вариатора гаиковысадочного автомата А411А, применяющегося в механизме подачи материала. Дано: ш= 10,5 1/с, Мс = 120 кгс-см, = 0,34 кгс-м с

с!ная размеры звеньев механизма, известными методами строим график (см рис. Ь, о), затем определив угол

а = arctg

10.5.о,34 = . S = 18° 20,

проводим касательную к данному графику под углом а к оси абсцисс.

ляем vmЛhT P° Р** = i (Р) У -Ф* определяем угол % = 10 5 и далее находим

2Ц = Фб + 10,1

57,3 + 10,5

5,1 52,3- 22,25 1,2 /52,3

57,3

2.10,52.0,34

/52,3 - 22,25 \

\ 57,3 ;

= 0,424 рад; ф2ц = 2422.

Для сравнения на рис. 6, а кроме графика изменения угла гр представлен график изменения этого угла (штриховая кривая) 140

полученного при кинематическом анализе механизма. В этом случае угол поворота ведомого звена за цикл движения автомата равен 17° 10, что составляет только около 70% величины ур2ц> определенной по формуле (13). Так как величина подачи материала пропорциональна углу и., то, следовательно, кинематический расчет приводит к значительно меньшим подачам.

ЗУБЧАТО-РЫЧАЖНЫЕ ВАРИАТОРЫ

Движение элементов вариатора. Общая схема вариатора совместно с приводным электродвигателем и рабочей машиной показана на рис. 7.

От электродвигателя Л (рис. 7, а) через вал 1 передается движение преобразующему механизму б, который, как ранее было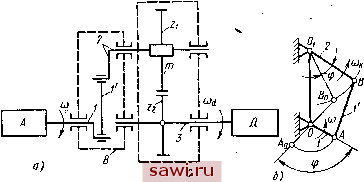

Рис. 7

установлено, может быть условно заменен шарнирным четырех-звенником (рис. 7, б). Колебательное движение вала 2 преобразуется выпрямляющим механизмом С в непрерывное вращательное движение ведомого вала 5. Механизм С включает в себя систему МСХ т и зубчатые колеса и Za- С валом 5 соединен приводной вал рабочей машины Д.

При исследовании этого вариатора примем следующие обозна-.чения: ф и со - угол поворота и угловая скорость кривошипа ОЛ;

(0 и е - угол поворота, угловая скорость и угловое ускорение коромысла OiB; р, со и - угол поворота, угловая скорость и угловое ускорение зубчатогоколеса z; - момент инерции зубчатого колеса z относительно оси вращения; Уд - момент инерции колеса и ведомого вала относительно оси вращения; - приведенный момент инерции механизма рабочей машины; - приведенный момент инерции ведомой части передачи; Мс - момент сил сопротивления; - передаточное отношение зубчатого механизма со - угловая скорость ведомого вала; Аф - угол поворота зубчатого колеса Zi за один цикл;

Аф - угол поворота кривошипа за один цикл; i - среднее передаточное отношение; k - число коромысел.

Движение механизма начнем рассматривать с момента, когда коромысло Ojfi (см. рцс. 7) находится в крайнем положении OiBg. Зная характеристику электродвигателя, размеры и массы звеньев бесступенчатой передачи, а также закон изменения сил сопротивления, методом, изложенным в предыдущем параграфе, строим графики величин © и г) в функции угла ф (рис. 8, а и б) для I и II групп преобразующего механизма (см. рис. 1, гл. 3). Если принять за звено приведения шестерню Zj, то уравнение движения ведомой части привода после расклинивания МСХ (в период выбега) будет иметь вид

(14)

Приведенный момент инерции

Приведенный момент инерции Jj рабочей машины в общем случае является величиной переменной, но чаще машины, в приводе которых применяют исследуемую передачу (например, токарный и фрезерные станки, некоторые виды конвейеров), имеют величину постоянной. При = const приведенный момент инерции ведомой части также будет величиной постоянной. В таком случае уравнение (14) можно представить в виде

(15).

Учитывая, что период выбега весьма мал и продолжается в течение сотых долей секунды, можно считать, что = const. При этом, интегрируя уравнение (15), будем иметь

®* - - Фй)-

(16)

Проведя касательную t-t (см. рис. 8, б) под углом

а = arctg

найдем точку касания b с кривой со = (ф), определяющую момент расклинивания, и точку пересечения d >с кривой угловой скорости смежного коромысла, определяющую угол поворота кривошипа, при котором МСХ смежного коромысла заклинится и ведомая часть будет двигаться вместе с коромыслом. Для построения графиков углов поворота зубчатого колеса в период

выбега ведбмой части в результате интегрирования уравнения (15) получим >

За один цикл движения закон изменения угла поворота зубчатого колеса Zi в зависимости от угла ф будет представлен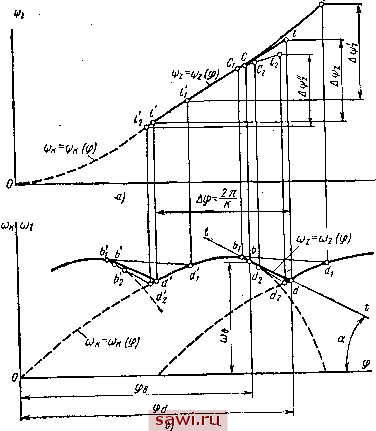

Рис. 8

кривой Id (см. рис. 8, а), а закон изменения угловой скорости (О, = (О, (ф) - в виде кривой dbd (см. рис. 8, б).

За время поворота кривошипа на угол Аф = -, соответствующий одному циклу, зубчатое колесо Zi повернется на угол Aij5, (см. рис. 8, а). При установившемся движении среднее передаточное отношение вариатора