При = 5 среднее передаточнбе отношение

(18)

Кривая изменения угловой скорости ведомого вала ш = = ш (ф) будет по своему характеру такой же, как и кривая оз = = (0 (ф), и может быть получена делением .ординат кривой

= z (ф) на передаточное отношение между зубчатыми колесами Zi и Za-

С изменением нагрузки, т. е. с изменением момента при постоянных значениях щц J, изменяется передаточное отношение передачи и равномерность вращения ведомого вала. На рис. 8, б кроме прямой bd угловой скорости со нанесены еще прямые bjffi и bdi, касательные к кривой = (л (ф), представляющие графики изменения в лериод выбега ведомой системы передачи.

Прямая bidi соответствует меньшему, чем в ранее рассмотренном случае, приведенному моменту М, а прямая bd - большему-приведенному моменту. Соответственно этим прямым построены графики одного цикла Лс/ и /гС/а углов поворота ф, dlbidi и dbdi угловых скоростей и. Угол AijJz соответствует прямой bidi, а угол Aif - прямой bd.

Из сопоставления величин AijJz и Atpl видно, что с увеличением приведенного момента уменьшается величина угла Аф, а следовательно, увеличивается передаточное отношение i и снижается угловая скорость ведомого вала. Сопоставляя прямые bd, bdi, bdi, можно заключить, что с увеличением нагрузки увеличивается наклон прямой = со (ф) и в связи с этим уменьшается равномерность вращения ведомого вала.

Неравномерность вращения ведомого вала. В зависимости от настройки передачи на то или иное передаточное отношение будет изменяться характер движения ведомой системы. Чтобы представить закон изменения угловой скорости ведомого вала и на всем диапазоне регулирования, на рис. 9 при помощи вышеизложенного метода построены графики изменения этой скорости (сплошные линии) в зависимости от угла ф для передачи, приводящей во вращение шпиндель токарного- станка, J = = 0,005 кгc м cЛ = 1,1 кВт. Графики выполнены для различных частот вращения п. ведомого вала при номинальной нагрузке. На рис. 9, а в качестве рабочего хода выбрано движение преобразующего механизма, когда направления вращения коромысла и кривошипа совпадают, а на рис. 9, б, когда коромысло и кривошип вращаются в разные стороны. На основании этих графиков можно сделать следующие выводы:

1 в области больших частот вращения ведомого вала (от 200 до 1000 об/мин) наблюдается выбег ведомой системы передачи в период спада угловой скорости коромысла;

2) при частоте вращения п < 200 об/мин движение происходит без выключения МСХ в период спада угловой скорости коромысла.

Рассматривая колебания величины угловой скорости ведомого вала в период установившегося движения (см. рис. 9), можно обнаружить, что эти колебания различны для различных частот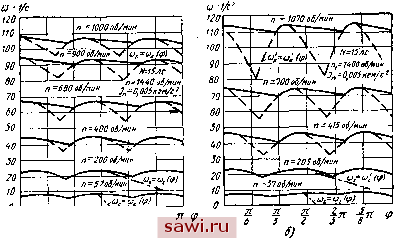

f f -f 1

Рис. 9

вращения n ведомого вала. Оценка неравномерности вращения ведомого вала может быть произведена через коэффициент неравномерности вращения б, определяемый по формуле

О =-л;;;-

Дф I и Йф

(19)

где 0)п,ах и Сй ,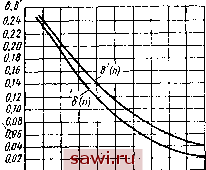

- наибольшее и наименьшее значения угловой скорости ведомого вала. На основании графиков, приведенньиь на ркс. 9, по вАфажению (19) .были вычислены значения коэффициентов неравномерности вращения ведомого вала б, соответствующего случаю, когда кривошип и коромысло преобразующего механизма в период рабочего хода движутся в одну сторону (см. рис. 9, а), - и коэффициента б для случая, когда кривошип и коромысло преобразующего механизма при рабочем ходе движутся в разные стороны (см. рис. 9, б). Результаты этих вычислений представлены в виде кривых на рис. 10, отображающих йзме.

О т 200 300 Ш 500 600 700 800 п.о5/мин Рис. 10

нение б и б в функции частоты вращения. Эти кривые наглядно показывают изменение равномерности вращения ведомого вала при полной нагрузке передачи на всем диапазоне регулирования частоты вращения п. С уменьшением частоты вращения ведомого вала коэффициенты б и б значительно возрастает, достигая при малых значениях п сравнительно большей величины (б = 0,25 при n = 57 об/мин). Коэффициент б на всем диапазоне частоты вращения ведомого вала меньше б, т. е. прямой ход дает несколько большую равномерность вращения по сравнению с обратным ходом.

Определение сил, действующих в вариаторе. Во время работы вариатора на его, элементы действуют силы полезного сопротивления, движущие силы, силы инерции движущихся масс и силы трения. Силы полезного сопротивления будем считать известными и постоянными.

На рис. 11, а точки Si, S, S3, s4, s5 и S изображают соответственно центры тяжести коромысел и пазового диска, а точки Oi, О2, о3, о4, Об и О - центры вращения этих звеньев. Зная крутящий момент Л4-на ведомом валу от сил полезного сопротивления, определим крутящий момент М от этих сил, действующий на коромысло:

(20)

где 1г - передаточное отношение между зубчатыми колесами; Ц2 - КПД зубчатой передачи; - КПД опор вала коромысла.

Крутящий цомент М передается тем коромыслом, которое в данный момент вращается с наибольшей положительной угловой скоростью и, следовательно, заклинено с ведущим зубчатым колесом Zi. Как видно на схеме, крутящий момент Mi передается коромыслом /. Кроме того, на это коромысло действуют силы инер-HHH/i и момент от сил инерции M i.

Сила Ji определяется из соотношения

J1 = -as,m, (21)

где as, - ускорение центра тяжести первого коромысла; - масса коромысла.

Эту силу можно считать приложенной в точке качания ki, расстояние которой от оси вращения

(22)

где /i - расстояние центра Si до оси вращения; У5--момент инерции коромысла относительно оси, проходящей через центр тяжести.

Рассмотрим период движения механизма передачи, когда угловое ускорение коромысла, передающего крутящий момент, положительно, так как в этот период силы, действующие на звенья, принимают наибольшие значения.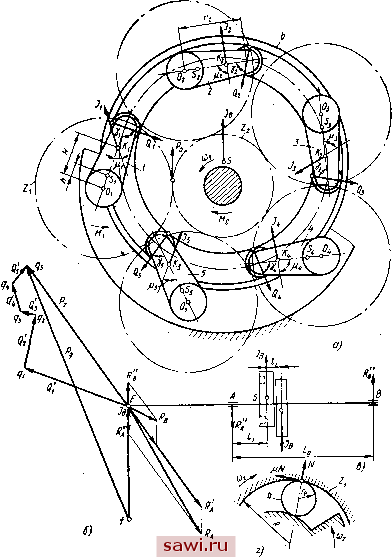

Рис. II

Величину приведенного к ведомому валу момента М от сил инерции движущихся масс ведомого вала с зубчатым колесом Z.2, четырех зубчатых колес Zi, вращающихся в рассматриваемый момент свободно на валах коромысел 2, 3, 4 и 5 и от движущихся масс рабочей машины, определим из соотношения

M.JAi-iJBi. + Ma, (23)

где е и eg - угловые ускорения соответственно ведомого вала и коромысла; - приведенный к ведомому валу момент сил инерции движущихся масс рабочей машины.

-la свободно вращающиеся зубчатые колеса действуют моменты от сил трения в МСХ.

Ролики, расклиненного МСХ (рис. 11, г) вращаются вместе с внутренней обоймой и под действием центробежной силы инерции давят на внутреннюю поверхность наружной обоймы. Возникающие на поверхностях соприкосновения роликов с наружной обоймой силы трения заставляют вращаться ролики вокруг их собственных осей и перекатываться со скольжением по поверхности наружной обоймы.

Если пренебречь действием прижимной пружины, то момент от сил трения в механизме свободного хода

Мр = iizni(R -r)wlR,

(24)

где [I - приведенный коэффициент трения, учитывающий скольжение и качение роликов; R - радиус наружной обоймы; г - радиус ролика; г - число роликов; т - масса ролика. Окружное усилие, передаваемое зубчатым механизмам.

2(Ме + Ми-4Мя,)

где - диаметр начальной окружности зубчатого колеса z. Подставляя значение из уравнения (23), получим

Ро = - (Мс + М, + 4Mpi, + Уде + 4У,еа1,).

(25)

Приведенный момент Мхк валу коромысла 1 от сил инерции движущихся масс

hz > .

ИЛИ, подставляя УИ из -формулы (23), получим

1 = 1ле + Ма + 4JeJ, + J, {Jz2 + sin . (26)

Действующий на коромысло / суммарный момент сил Л/ = М + Ml4Mf,

или, выражая М и УИ через их значения соответственно формулам (2Q), (26), получим

+ ЛЛЛег-Ь iltA sin [Xi). 148

Так как величина r[J.J sm \ii по сравнению с другими величинами правой части незначительна, а величина мало отличается от единицы, то, можно приближенно принять

y.eat, р 11,1,82, + ЛЯ sin Hi (28)

и. тогда

(29)

Коромысла 2, 3, 4 VI 5, свободно вращаясь в рассматриваемый момент вокруг своих осей, находятся под действием сил инерции

(30)

h = - asm; J3= - asitn;

li = - asiin; /5 = - as5K- J

Их можно считать приложенными в точках k., kg, k, (точки качания), находящихся на расстоянии Я от оси вращения коромысел.

На пазовый диск 6 действует центробежная сила инерции Уд, величина которой равна

(3-1)

Уд = Отдоле,

где т-д - масса диска 6.

Зная силы 1нерции и силы полезного сопротивления, определим усилия, действующие в кинематических парах передачи.

Для определения усилий Qj, Q, Q3, Q4, Qb> действующих со стороны контактной поверхности диска 6 на ролики коромысел, составляем условия равновесия каждого из коромысел в отдельности. Уравнения равновесия представлены в виде уравнений моментов относительно осей вращения коромысел:

1 Гз sin 7i r2Цzz sm у

Q2 =

JH sin Ц2 . Г2 sin 72

JgH sin Из . Г2 Sin 7з

(32) (33)

Q JjH Sin jij . Q JjH sin Ц5 Г2 sin 74 /-2 sin 75

.Сила Рд, действующая на диск и воспринимаемая опорой качения диска, определится по векторному уравнению

Рд = Уд + Ql + Q2 +, Qs -I- Q; -f Ql

(34)

где $1, Q2, Qs, Q4 VI Qs - слы давления роликов коромысел на диск 6.