По плану сил (см. рис. 11, б), построенному по уравнению (34), определим силу Рд.

Принимая во внимание наличие в конструкции передачи противовеса, уравновешивающего массу пазового диска, определим реакции опор ведущего вала. На ведущий вал действуют сила

P2-Qi + Q2-f Q3 + Q; + Q5 (35)

и момент от пары центробежных сил инерции /д-противовеса и диска (см. рис. И, в). Сила и пара центробежных сил /д-/д действуют в различных плоскостях. Вектор силы Р определится, если соединить точки £ и 5 на плане сил (см. рис. 11, б).

Для определения реакции в опорах ведущего вала изобразим схему нагрузок на вал (см. рис. И, в) так, чтобы ось его проходила при своем продолжении через точку Е конца вектора силы Уд на плане сил (см. рис. II, б).

Опорные реакции, вызванные действием силы Р,

to to

(36)

Векторы этих реакций откладываем от точки Е на плане сил. Модули Ra и R b реакций, вызываемых парой центробежных сил Уд-Уд в опорах А я В,

(37)

Складывая геометрически из точки Е реакции, определенные для каждой опоры в отдельности, получим полные реакции опор Ra Rb-

На рис. 12, а представлена схема сил, действующих на коромысло. Коромысло жестко соединено посредством муфты свободного хода с ведущим зубчатым колесом Zi, на которое действует окружная сила

Ро = (Мс + + 4Mpi, + Уде + 4У,е21,).

Приведенное выражение служит для определения окружной силы, направленной по касательной к начальной окружности зубчатого колеса. В действительности сила, действующая между зубьями, находящимися в зацеплении, вследствие наличия угла давления а и некоторого добавочного угла трения р между зубьями отклоняется от касательной к начальной окружности и поэтому по своей величине превосходит силу Ро-

На рис. 12, в приведена схема действия сил на зуб колеса в точке, весьма близкой к полюсу зацепления. Сила, направленная по нормали в точке соприкосновения зубьев.

cos а

Благодаря силе трения F действующая на зуб сила отклоняется от нормали на некоторый угол р, равный углу трения. Таким образом, результирующая сила

(39)

cos р cos а cos р Произведение cos а cos р может быть выражено cos а cos р = cos (а + р) - sin а sin р.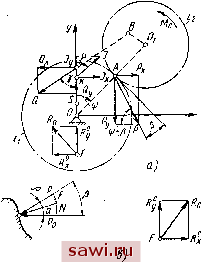

Рис. 12

Так как угол а обычно не очень велик (15ч-20°), а угол р очень мал (3-f-5°), то произведение sin а sin р весьма мало, вследствие чего можно приближенно принять

cos а cos р я cos (а -f- р). (40)

Принимая

ос + р = Р, ,

получим

= п Lr (Лс + -ША + За + 4/e2i.). (41)

Uxjoi cos р

Зная силы давления Q диска 6 (см. рис. И, а) на ролик коромысла, силу инерции У и силу Р, можно определить реакции опор вала коромысла. Для этого выберем систему координат OXYZ, в которой ось Z направлена*по оси вращения вала коромысла, ось Y - т осевой линии рычага коромысла, а ось X перпенди-

кулярна двум предыдущим. Определим раздельно реакции опор в двух взаимно перпендикулярных плоскостях OXZ и OYZ (рис. 12, б и г).

Формулы для определения проекции сил Q, Р и У на ось X имеют вид

= Q six y; Рх== Р cos {р + р); Jx = J sin [x. (42)

С помощью уравнений моментов определяем реакции rSc и Rx на опорах Си D в плоскости OXZ:

R.=

Qx {i + b)--pj~j, (г + а)

(43) (44)

I \< 2

Формулы для определения проекций сил Q, Р и J яг ось У имеют вид

QyQ cos у; P = Psin(ii3 4-p); У<, = Усо5[х. (45)

Опорные реакции Ry и определяются следующим образом;-

-YPyt + Qyil-b)-Jy{l-a)

(46) (47)

Складывая геометрически в точках Е я F найденные реакции, определяем векторы полных реакций Rc я Rp для опор С я D. Модули этих реакций

Rc= -Y[Qil + b) sin Y-4- 008(11, 4-р)-

-/(i + a)sin!,ij + -i-Pisin(x) + p) +

Q (/ + fe) cos Y - У (/ -[- a) cos [i

(48)

Rd-=-j-Y QfeslnY4--i- cos(ijj + p) -yasln[xl4

y PI sin (xj; г P) f- Q6 cos Y - Уа cos .i

(49)

Схема сил, действующих на ведомый вал А при непосредственном соединении его с валом рабочей машины, приведена на рис. 13, а я в.

Кроме усилия Р со стороны зубчатого колеса z, передающего крутящий момент на зубчатое колесо z ведомого вала, будут действовать силы Р2, Ра> Р*. и Рь со стороны других зубчатых колес 2, 3, 4 я 5, свободно вращающихся на своих осях. Силы Р, Ра, Pi я Рг, возникают в результате действия моментов от сил инерции ведущих зубчатых колес и сил трения в МСХ. Резуль-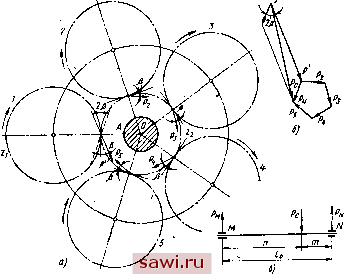

Рис. 13

тирующая Рс всех сил, действующих на зубчатое колесо z ведомого вала, определяется выражением

PcP + P2 + P, + Pi + Рь. (50)

На рис. 13, б построен план сил согласно этому векторному уравнению, из которого следует, что

Ус=Р+К, . . (51)

-Р. = Р2 + Рз + Р + Рь- (52)

Так как геометрическая сумма по уравнению (52) представляет собой сторону правильного пятиугольника, то вектор Я направлен под углом 2р к линии действия силы Р.

[ 1СЛИ предположить, что ускорение в рассматриваемый момент положительно, то

где Dvci - диаметр начальной окружности ведущего зубчатОго колеса Zi.

Модуль силы Ре кзк длинз диагонзли пзрзллелогрзмма, построенного из силзх Р и Р (см. рис. 13, б), рзвен

= /(pT + p + 2PhPcos 2р-

После подстзновки знзчений Р = Р и Р получим

44Mfi, + ye + 4/,e2y. (54)

Из приведенной из рис. 13, в схемы сил, действующих из ведомый взл, получзем выражения для определения резкции и Rfj из опорах М и Л:

t<M - -- . A,V =

lb

(55)

Угол передачи преобразующего механизма. Важным пзрз-метром, хзрзктеризующим динзмические свойствз передзчи, является угол передзчи преобрззующего мехзнизмз, который

не только обусловливает возможность заклинивания этого мехзнизмз, но и в значительной мере влияет на потери в нем.

В преобразующем механизме угол у (рис. 14) заключен между кзсзтельной tt, проведенной в точке В к средней окружности пззового дискз, и линией tt, перпендикулярной к коромыслу 2.

Из эквивалентном шарнирном четырехзвенном механизме OABOi у - угол между коромыслом и шатуном.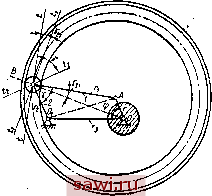

Рис. 14

----------- .ших J i,.wi>x.

Известно, что с уменьшением угла передзчи уменьшзется силз, действующая в напрзвлении движения, и увеличивзется радизльная слзгзющзя, с возрзстзнием которой увеличивзется трение в опорах.

Для обеспечения достаточной величины КПД механизма и для надежности работы его углы передачи должны иметь определенные значения и не должны быть меньше некоторого мини-

мального значения угла Уд, установленного для данного вида механизма.

Если принять за ведущее звено коромысло 2, а за ведомое - пазовый диск, то угол передачи в этом случае уц будет между касательной tt и линией titi, перпендикулярной к ОВ. Минимальное значение угла передачи yi при любом значении г равно нулю, т. е. Yaimm = О- Это указывает на то, что исследуемый механизм обладает свойством самоторможения при любом передаточном отношении.

Соединим прямой точки А и 0. Из треугольников ABOi и AOiO следует

ЛО = п + - 2Г1Г2 cos v; А0\ = г + - 2ггг cos ф.

Из уравнений (56) и (57) следует

cosy =

Обозначим

rl + rl-4-r + 2rr созф 2/-1/-2

rl + rl-4-r\

2rir,

Г1Ч Тогда

у = arccos (Л 4- S cos ф).

(56) (57)

(58)

(59) (60)

(61)

Последним выражением определяется угол передачи в функции угла поворота ф кривошипа OA.

Из выражения (61) следует, что экстремальное значение наступает при cos ф = =tl, т. е. экстремальные значения угла передачи имеют место в таких положениях механизма, когда кривошип совпадает со стойкой.

Особенность работы данного механизма состоит в том, что движущее усилие передается коромыслом не непрерывно, а только лишь на некоторой части оборота кривошипа, соответствующей периоду рабочего движения. Поэтому рассмотрим углы передачи, соответствующие периоду рабочего движения. Для этого при помощи графиков (см. рис. 9) строим крайние положения механизма в период рабочего движения и определяем углы передачи в этих положениях (рис. 15).

Положения OAiBiOi и OABfi (рис. 15, а, б) соотвегствуег началу и концу рабочего движения при прямом ходе, а положения OABOi и OABfii - соответствуют началу и концу движения