при обратном ходе; углы Vmin и vax обозначают минимальный и максимальный углы передачи для периода рабочего движения при прямом ходе, а Ymin и Ymax - минимзльный и максимальный углы передачи для периода рабочего движения при обратном ходе.

Построения произведены для различных значений г. В результате найдены зависимости углов передачи Vmln, Vmax, Vmin, Vmax

от частоты вращения п

tlha. (рис. 15, в).

Из этих зависимостей следует, что:

наименьшее значение Минимального угла передачи в период рабочего движения для прямого хода больше, чем для обратного;

минимальные углы передачи Vmm и Ymin увеличиваются с уменьшением г, причем это увеличение сильнее сказывается для Ymin;

минимальный угол передачи Vmin при прямом

ходе на всем диапазоне частот вращения п больше, чем минимальный

S 60

2 70 1

Рис. 15

иОО 600 п, об/мин

то юоо

угол передачи Vmin при обратном ходе, что указывает на целесообразность использовании прямого хода в качестве рабочего, так как КПД передачи при этоМ должен быть выше. Это утверждение требует экспериментальной проверки, ибо на КПД передачи влияет еще лът ряд факторов, которые теоретически учесть не представляется возможным.

Уравновешивание механизма вариатора. При движении механизма вариатора на его звенья действуют динамические силы, которые создают дополнительные силы трения в кинематических парах, вибрации и дополнительные напряжения в звеньях механизма. Чтобы ликвидировать столь вредное воздействие динамических сил, их по возможности уравновешивают, подбирая соответствующие массы звеньев и устанавливая специальные противовесы.

Задача уравновешивания динамических сил сводится к уравновешиванию сил инерции.

Расположим оси Х и Y (рис. 16) в плоскости, параллельно которой происходит движение* механизма вариатора; ось Z на-

правим перпендикулярно к этой плоскости вдоль оси вращения кривошипа OA. Для уравновешивания сил инерции и моментов от сил инерции необходимо подобрать массы звеньев так, чтобы были удовлетворены следующие условия:

Р5 = const;

2 т,2;Л,. = const;

S m(Ziyi = const.

(62) (63) (64)

где Р5 - радиус-вектор, определяющий положение центра тяжести движущихся масс механизма; 2 ггл;,- - центробежный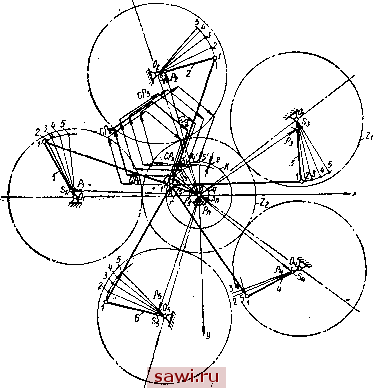

Рис. 16

момент инерции движущихся масс механизма относительно плоскости хг\ m-iZiyi - центробежный момент инерции движущихся масс механизма относительно плоскости yz.

Уравнение (62) выражает необходимое условие уравновешивания сил инерции, а уравнения (63) и (64) - условие уравновешивания моментов сил инерхии. Ввиду того, что исследуемый механизм весьма компактен в направлении оси Z, моменты сил

инерции сравнительно невелики. Поэтому в дальнейшем рассматривается только вопрос уравновешивания сил инерции.

Положение центра тяжести механизма определяется из выражения

Ps =

Записывая это выражение в развернутом виде для механизма передачи, получаем

5 5

Ps =--

где - масса ведущего колеса z; - радиус-вектор, определяющий положение центра тяжести ведущего колеса; - масса коромысла; р,- - радиус-вектор, определяющий положение центра тяжести i-ro коромысла; /Пд - масса пазового диска; г - радиус-вектор центра тяжести пазового диска (всегда равный длине кривошипа и направленный вдоль него от точки О); 2 - суммарная масса всех движущихся звеньев механизма.

Вследствие расположения осей ведущих зубчатых колес по окружности на одинаковом расстоянии одна относительно другой

гРгО. В ЭТОМ СЛучаС

величина

Ps =

Умножив обе части

(65)

уравнения (65) на

д I

Обозначим

S i - . ...

Тогда

получим

Г + С S +с (PI+P2 + p3+ р4+Ро)-

(66)

Из точки о (см. рис. 16) произведем сложение векторов согласно векторному уравнению (66). Результирующая этой геометрической суммы ps представляет собой радиус-вектор центра тяжести механизма в масштабе (Лр -

Величина радиус-вектора центра тяжести механизма

Ps == [ApPs =

Точка S представляет собой центр тяжести механизма. Траекторию точки S при движении механизма можно найти, определив предварительно годограф вектора р. Для этого построим геометрические суммы векторов по уравнению (66) для различных положений механизма. На рис: 16 в результате построения получен годограф вектора р в виде кривой 2, 3, 4, 5 для угла поворота кривошипа, равного Кривая изменения вектора ps будет повторяться каждый раз при повороте кривошипа на фазо-выи угол -g-; при этом она будет сдвинута на этот угол по ходу

движения кривошипа. Годограф вектора ps представляет собой кривую k, которая незначительно отличается от окружности, радиус которой равен р. По годографу вектора р, пользуясь выражением (67), получим траекторию q центра тяжести механизма, которая еще в меньшей мере будет отклоняться от окружности. Эту траекторию в дальнейшем будем считать окружностью с радиусом Ps- Вектор р, как показано на рис. 16, почти совпа-.дает с направлением вращения кривошипа г. Все это дает основание принять движение центра тяжести механизма происходящим по окружности с угловой скоростью кривошипа е>1. Из построения следует, что

- (г + е) Отд Ps---vv-

2j nti

S pi-

(69)

Неуравновешенная сила инерции механизма Рн = со?р5

Подставляя значение р из формулы (68), получим P = a)?/nд(r-f е).

Чтобы вычислить неуравновешенную силу инерции механизма, необходимо в дополнение к известным величинам т и г располагать значением е. Последнее можно определить, построив геометрическую сумму по уравнению (69) для одного .какого-либо произвольного положения механизма.

Для механизма передачи с г% = 13 мм величина Pj, равна 58 кгс при = 1500 об/мин и 232 кгс при == 3000 об/мин.

Такая значительная величина неуравновешенной силы инерции обусловила применение уррновешивающих устройств в передачах более поздних конструкций.

Так как центр тяжести механизма с некоторыми допущениями принят вращающимся вокруг оси, проходящей через неподвижную точку О, то уравновешивание достигается установкой противовеса с массой /Пп, расположенного на продолжении линии SO так, что величина силы инерции противовеса

(70)

а)?/Ид (г 4- е) = а)?/Ппрп,

откуда

где Рп - расстояние центра тяжести противовеса от оси вращения.

В процессе регулирования передачи с изменением величины г от О до Гп,ах однозначно изменяется величина в от О до еу..

Чтобы осуществить уравновешивание при любом передаточном отношении передачи, нужно выполнить уравновешивающее устройство так, чтобы уравнение (70) удовлетворялось при любом значении г, т. е. необходимо, чтобы при постоянной массе противовеса уравновешивающее устройство обеспечивало изменение в зависимости от г по уравнению (70). Точное выполнение этого условия связано со значительными конструктивными усложнениями. Для простоты конструкции уравновешивающие уст,ройства в существующих импульсных передачах выполняются так, что величина Рд всегда равна г.

Определим массу противовеса для уравновешивания силы инерции при г - Гп,ах- В этом случае

д (/ max + шах) - Щ/ шах

откуда

с уменьшением г уменьшается величина е. Величина отношения изменяется при регулировании весьма незначительно

и не оказывает существенного влияния на неуравновешенность, тем более, что сама неуравновешенная сила инерции уменьшается пропорционально уменьшению г.

Противовес с массой, определенной по формуле (71), при испытании передачи оказался весьма эффективным при всех значениях г.

Таким образом, чтобы определить массу противовеса, необходимо прежде всего найти величину вах. построив для этого геометрическую сумму векторов по уравнению (69) при г = г для одного положения механизма, а затем по формуле (71) подсчитать величину /Пп. Отношение у существующих передач

равно 0,1-0,12, и, следовательно, /Пп = (1,1--1,12)/Пд.

Глава 6

ДИНАМИКА

МЕХАНИЗМОВ СВОБОДНОГО ХОДА

ТЕОРИЯ СВОБОДНОГО ДВИЖЕНИЯ РОЛИКОВЫХ МСХ

В подавляющем большинстве импульсных вариаторов в качестве МСХ применяются роликовые механизмы с цилиндрическими и эксцентриковыми роликами, поэтому в дальнейшем приводятся теория и расчет только этих механизмов..

Функционирование роликовых МСХ можно представить так: включение - заклинивание механизма происходит при вращении звездочки 2 (рис. 1) относительно обоймы 1 по часовой стрелке или, наоборот, обоймы относительно звездочки против часовой стрелки. При этом ролики заклиниваются между звездочкой и обоймой, соединяя в одно целое основные элементы МСХ.

При относительном движении обойм в противоположном направлении происходит выключение, расклинивание механизма; при этом возможно свободное движение обойм.

Ведущие и ведомые звенья МСХ импульсных вариаторов движутся циклически. Полный цикл движения роликовых МСХ можно разбить на следующие основные периоды: свободного хода, заклинивания, расклинивания.

Под периодом свободного хода понимают время движения механизма, когда обоймы не заклинены и движутся одна относительно другой. При этом ролики под действием пружин хотя и соприкасаются с рабочими поверхностями обойм, но остаются незаклиненными между ними. Свободный ход механизма продолжается с момента окончания процесса расклинивания до момента начала заклинивания. Чаще всего в этот период механизмы свободного хода представляют систему с двумя или тремя степенями свободы.

Если обозначить ©i угловую скорость обоймы, а ©з - угловую скорость звездочки, то в течение всего периода свободного хода (рис. 1) должно выполняться условие

©1 > ©2-

Направление угловой скор(сти ©i при этом принимается за положительное. Законы движения роликов в течение свободного

М. Ф. Мальцев