хода, как будет показано ниже, обусловливаются конструкцией механизма, законами движения обойм и целым рядом параметров механизма. Очень важным является нормальное протекание динамических процессов, обеспечивающих нормальное функционирование механизма как в период свободного хода, так и в последующие периоды.

Действие динамических нагрузок на элементы МСХ вызывает колебательные процессы в период свободного движения и может привести к. нарушению контакта ролика с рабочими поверхностями обойм. Указанное действие проявляется наиболее интен-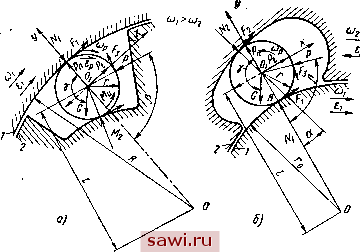

Рис. 1

сивно в вариатора), приводящихся непосредственно быстроходными электродвигателями, полный цикл которых осуществляется в течение сотых долей секунды.

Колебание роликов не только повышает потери в период свободного хода и интенсифицирует износ, но и нарушает нормальное протекание процесса заклинивания.

Если нарушение контакта ролика с обоймами не всегда пагубно, сказывается в период свободного хода, особенно при отсутствии колебаний, то в момент начала заклинивания оно недопустимо. Условие контакта ролика с обоймами в*конечной фазе периода свободного хода следует считать одним из главных условий правильного взаимодействия основных звеньев МСХ. Невыполнение указанного условия ведет к запаздыванию начала процесса заклинивания или даже к полному отсутствию его. При этом возможно возникновение больЩих динамических нагрузок вследствие несвоевременного заклинивания а, следовательно, интенсивный износ элементов механизма и нарушение всей работы машины в целом.

Период свободного хода у МСХ импульсных вариаторов увеличивается с увеличением амплитуды колебания ведомого звена преобразующего механизма. Во избежание интенсивного износа в этот период необходимо выбирать параметры МСХ так, чтобы ролики вращались в период свободного хода, в противном случае увеличатся потери и появится местный износ роликов в виде лысок.

Свободное движение МСХ с цилиндрическими роликами. Схемы механизмов с действующими на ролик силами для наиболее общего случая движения, когда обойма и звездочка вращаются с переменными угловыми скоростями и Oj, а ролики вращаются вокруг своей оси сугловой скоростью Юр, показаны на рис. 1, а (механизмы с внутренней звездочкой) и на рис. L, б (механизм с наружной звездочкой).

Введем следующие обозначения:

Р, Рз> /з и рз - усилие прижимной пружины, сила трения, коэффициент трения и угол трения на поверхности контакта ролика и прижима; N, F, f, pi и - нормальная реакция, сила трения, коэффициент трения, угол трения и коэффициент трения качения на поверхности контакта ролика с обоймой;

р2< f 2 И р2 - нормальная реакция, сила трения, коэффициент трения и угбл трения на поверхности контакта ролика и звездочки; G и m - вес и масса ролика; g - ускорение силы тяжести; / - расстояние между центрами ролика и обойм; Р - угол между направлением усилия Р и линией 00, соединяющей центры механизма и ролика, угол установки прижима; у - угол между линией действия силы тяжести и линией OOi, Si, ва, бр - угловые ускорения обоймы, звездочки и ролика; Р а Р - нормальная и тангенциальная силы инерции; ,Ур - момент инерции ролика относительно его оси.

Запишем уравнения динамического равновесия ролика, проектируя все силы на координатные оси X и F (см. рис. 1):

2 г/ = +Л?1 -i- Р + Р cos р ± fgP sin р ± Л?2 cos а т

Т /гЛ2 sin а - G cos(180° - у) = 0;

2 д; = fiNi + - Р sin р ±/зР cos р + Nina +

+f гЛг cos а - G sin (180° - y) = 0.

Данные уравнения справедливы как для механизмов с внутренней звездочкой (см. рис. 1, а), так и для механизмов с наружной звездочкой (см. рис. 1, б), с тем лишь отличием, что у некоторых членов знаки будут различны. Необходимо заметить, что в этих уравнениях и в последующих выражениях при исследовании механизмов с единичным расположением роликов верхние знаки соответствуют механизмам с внутренней звездочкой, нижние - механизмам с наружной звездочкой. В результате совместного

решения уравнении равновесия находим нормальные реакции Ni и N2-

-Р [(1 + /2/3 sin (Р ± а) ± (2 - /з) cos (Р ± а)] ± ± Р (sin а + /2cos а) - Pt (cos.а - /2 sin а) +

а; +G[sin (у ± к) ± 2C0S(y ± )] .

1 (I-/1/2) sina + (/i + /2)cosa

Р W - Ш sin р + (/1 + /з) cos р] + hPn ~Pt +

N, =

+ G (sin Y + 1 cos 7)

(1~Ш sin a + (1 +/2) cos a

/2V2

8p/p /3

Это справедливо при условии вращения ролика rhN,~

Условия контакта ролика с обоймами запишутся в виде неравенств yVi>0 и Л?2>0 или, принимая во внимание, что силы инерции

(4) (5)

(6) (7)

Рп = т1(4, Р( - тЫ,

на основании уравнений (1) и (2) получим

т/[(cos а -/2 sin а) 82 + (sin а-f/2 cos а) а)]-

р -G[sin (7± а) ±/2Cos(7± )] .

(l-f/2/3)sin(P±a)±(/2-/3)cos(P±a) ml (82 ±Люр - G (sin 7 - ft cos 7) , (l-fiWsinp + (fi-f Wcosp

где - усилие прижимной пружины, гарантирующее контакт ролика с обоймой; Р - усилие пружины, гарантирующее контакт ролика со звездочкой.

Как видно из уравнений (6) и (7), по мере изменения угловой скорости 2 и углового ускорения Cg, а также угла 7 величины Р и р2 в период свободного хода будут изменяться. Следует заметить, что угол Y. определяющий направление силы тяжести относительно радиуса механизма 00, одновременно является и углом поворота звездочки.

Естественно, для того чтобы иметь контакт ролика с обоймами в течение всего периода свободного хода, следует обеспечить в механизме свободного хода прижимное усилие Р, которое было бы больше или равно наибольшей из максимальных величин Pi и Pj.

Условие вращения ролика без учета трения качения по рабочей поверхности обоймы на основании выражения (3) имеет вид

Р<

После подстановки в это неравенство значений нормальных давлений Ai и из уравнений (1) и (2) и замены сил инерции Р и Р их значениями, определенными по формулам (4) и (5) условие вращения ролика примет вид

> в й)2<(1)2

= Л, /л2р + 382 ± AiJpEp ± С 1/2 (sin Y fi cos y) -

-fi[sin(Y±a) itfacos (Y±a)]},

где ©1 - предельная угловая скорость звездочки, при которой ролик начинает вращаться вокруг своей оси:

Ах=[т1 (fi sin а + 2fif2 cos -)

Л, =

Л =

±/2 1(1 - fifs) sin Р + (/1 + h) cos Р ] ±

fs t(l - f if 2) sin a + (f 1 + /2) cos a ] +

+f X t(l + f 2/3) sin (p ± cc) ± (/2 - fs) cos (p ± a) ];

m/ [±:fi (cosa -/2 sina) T/2];

Л4 = 4-- 1) + +

Неравенство (9) обусловливает такое значение угловой скорости ©2 звездочки, при котором обеспечивается, вращение ролика во время свободного хода. Для механизмов с внутренней звездочкой вращению ролика соответствует диапазон угловых скоростей ©2 от предельной угловой скорости © и выше, а для механизмов с наружной звездочкой вращение ролика наблюдается при угловых скоростях ©2, меньших предельной угловой скорости ©. ,

В тех случаях, когда угловая скорость ©2 периодически изменяется, переходя через нуль, ролик может вращаться с остановками.

В качестве примера на рис. 2 приведены графики изменения угловой скорости ©2 и ©I для МСХ зубчато-рычажного импульсного вариатора (см. гл. 1, рис. 29) за полный цикл его движения в функции угла поворота кривошипа. В период увеличения угло- вой скорости ©2 за время поворота на угол ф1 угловая скорость ©2 < ©, и, следовательно, ролик не вращается относительно звёздочки. При повороте кривошипа на угол фз ролик будет вращаться, так как ©2 > ©. В период, соответствующий углу поворота фз, угловая скорость принимает мнимые значения; это. указывает на то, что условие вращения ролика выполняется даже при отрицательном значении центробежной силы инерции Р , всегда имеющей положительное значение. Итак, мнимому значению ©I будет соответствовать фаза вращения ролика. Рассматривая последующие периоды умякла, видим, что после периода за-

клнненного состояния, осуществляющегося за угол поворота ф, насту41ает период выстоя ролика при повороте кривошипа на угол Ф5 в силу того, что по абсолютной величине cOg < сй .

Момент сил трения в .период свободного хода не только обусловливает потери в МСХ, но и нри значительной своей величине

вызывает обратное движение ведомой части привода при нензгру-женном вариаторе.

Если при движении механизма неравенство (3) выполняется, то исходя из предположения, что качение ролика по поверхности обоймы осуществляется без скольжения, роликовый МСХ в период свободного движения можно уподобить фрикционному дифференциалу; тогда угловая скорость ролика

р = 2 -f -©г).

(10)

Момент сил трения Ml одного ролика будет слагаться из моментов сил трения на поверхностях соприкосновения ролика со звездочкой и прижимом и момента трения качения ролика на рабочей поверхности обоймы, т. е.

Mi = r{f2N2 + hP)kiNi.

Принимая во внимание уравнение (10), определим приведенный к обойме механизма момент сил трения одного ролика: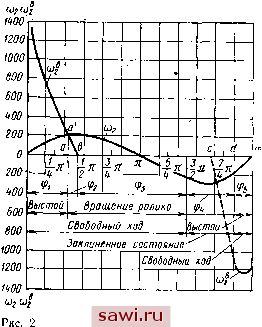

(11)

где k

Подставляя значения и Л из уравнения (1) и (2) в уравнение (11), получим

n-={j+-=t/)(FiP-f ti2P -F3+h4g). -166

Здесь величины p-i, р-г и будем называть приведенными коэффициентами трения механизма свободного хода; они равны:

>1

- Ш sin (к ± Р) ± (/2 - /з) cos (к ± Р)

(I-fih) sia а+(fi + fi) cos а

(12) (13) (14)

(1 - fih) sma+Qi + / ) cos а

fs [( - Ш sin g + (fr+ fi) cos a]. (1-Ш sina4-(fi-i-Wcosa

±k (sma + li cos a) + fj . ~ (1 - hh) Sin a+{h + h) cos a

A(coscc -2 sin g)+/г ~ sin a + (/i-i-Wcosg

k I sin {y±a)+ h cos (-y ± )] -I- 2 (sin -y + /i cos -y) ~ (1 - hh) sin a+(h + h) cos g

Суммарный момент сил трения всех роликов

= + /--/) Z ((iP +>2 - \1гР* + t 14g) .

где Z - число роликов.

Так как ролики в механизме расположены строго на одинако- вых расстояниях один относительно другого, то можно принять

Sfgo.

Тогда момент сил трения в период свободного хода в общем случае движения

Лт Z[-фг +г ±l) [iiiP -f ml{ii2(4- f382)], (15)

a мгновенная мощность Л, затрачиваемая, на трение,

Лт = 2 (т + + - 1362)] ((01 - г). (16)

Последние соотношения указывают на то, что потери в МСХ импульсных вариаторов характеризуются тремя приведенными коэффициентами трения p.i, Цг и Цз.

На основании формул (12), (13) и (14) можно сделать вывод, что приведенные коэффициенты трения МСХ можно уменьшить в основном за счет уменьшения коэффициентов трения На поверхностях контакта ролика с обоймами и прижимом, ибо угол р, как будет показано ниже, следует назначать из условия минимального усилия Р прижимно! пружины, а угол а - из условия заклинивания.