Под действием центробежной силы инерции ролики стремятся оторваться от внутренней обоймы, вследствие чего может нарушиться контакт ролика с внутренней обоймой. Чтобы этого не. произошло, необходимо прижимную пружину выбирать соответствующей жесткости. Следует отметить, что пружины малой жесткости могут не обеспечить контакт в начальный период заклинивания, и заклинивание будет происходить с запаздьшанием или вовсе не осуществится. Прижимная пружина большой жесткости приводит к повышенным потерям в период свободного хода.

Условие контакта ролика с внутренней обоймой:

или из уравнения (37)

(h + R sin ц) Р - PR Sin + (R cos p - ls) Pt + +AR Sin 7 - Us Sin {Y рд)1 G 0.

(38)

Прижимное усилие, создаваемое пружиной и гарантирующее контакт ролика с обоймами в начале заклинивания,

m/os in p,Q)-( cosPi-/os) бз]- .

р --[Д sin у - las sin (у - Pi)] G , ,

----h,+ R sin --

Если ролики прижимаются к обоймам под действием момента Мпр, то величина

Мпр = m/os [R sin Р1СЙ3 - {R cosPi - /os ) з] - .

-G[/?sinV-/osSin(Y-p,)], (40)

где co3, 83 - угловые скорость и ускорение роликов в момент начала заклинивания.

Максимальное значение нормального усилия iVjmax ь течение одного оборота будет иметь место при угле у который определится из нахождения экстремума, аналогично углу у:

(41)

На основании уравнения (39) определим угловую скорость роликов со, при которой все ролики оторвутся от внутренней обоймы:

/ (/i + ;?sinp,) P+mlos {Rcosfii - los) е + (й \/ +\Rsin r-hssm (Y -Pi)] G

mRlos sin Pi

(42)

Здесь 8 - угловое ускорение роликов в момент их отрыва от внутренней обоймы.

Уповая скорость роликов о) найдется из дифференциального уравнения движения системы роликов в. период свободного хода

(43)

где момент инерции всей системы роликов; Mi - суммариьш момент сил трения F, М, - суммарный момент сил трения F,. Используя формулы (35) и (36), получим

Ml - t fii =

Мг ti №0 = Л

zf,R (fliP + &iP + CiPi) + hRG Ъ di

; (44)

; (45)

где z - число роликов; h коэффициент трения на поверхности соприкосновения роликов с наружной обоимощ

Л =

/? (Sin Ро +/2 cos Ро) - fao -

а R (sin Рз -f /2 cos Рз) - h (cos Ро -/з sin Ро) -

- /2Г0 cos fx;

Й1 = Р (sin Pa -f /2 cos P2) -/2/-0 cos pi;

Ci = (cos P2 - /2 sin Pa) - Us (cos Po - /2 sin Po) -

- afoSinPi;

di = R (sm 72 - /2 90s 72) - los (sin Ti cos Po - -/2 sin 7i sin Po)-f-/20 cos 7;

= h + R sin [i; = R sin p; = R cos Pi - Us, 2 = sin 7 - los sin Tl-

Так как ролики расположены в кольцевом пространстве между обоймами на равных расстояниях один относительно другого, то можно принять

= О и f da = 0.

Принимая во внимание последние соотношения и выражая силы инерции Р и Р в формулах (44) и (45) через их значения

Pn = >nlos4>; Pt==>nU-i *

найдем моменты сил трения M, = AhzR [ml (v> + Ci4)+fliP

(46) (47)

. мГ3 Ml и Мз из формул (46) и (47) в выражение (43), получим \ / к

dt Jc - Azmlos {hRci - f.,roc2)

= 0.

Обозначим постоянные

Az {fiRbi - hri) mlos . 1 Jc - AzmlosihRci - fzroc)

Az {hRay-Ш Jc -AztnUsifrRcx-tirfft) после чего запишем

Разделив переменные, проинтегрируем это уравнение:

t (Л

arctg(О-arctg / о

(48)

Здесь ©о - угловая скорость, соответствующая началу свободного хода при выполнении неравенства ©i :> © > ю. Решив уравнение (48) относительно ©, получим

© =

= tg (arctg 0)0 +/,-Р

(49)

Мгновенная мощность /V, затрачиваемая на трение, определится на основании формул (46) и (47):

= Az \f,R [tnlos (&! + с,г) аР] (а>, - ©) +

+ /20 [mlos (се - Ьоу ) 4- /I ( - ©2)) (50)

При ©1 > © < ©2 дифференциальное уравнение движения роликов примет вид

Л = м1 + А?2.

Интегрируя это уравнение, произведя выкладки, аналогичные предыдущему случаю, определим угловую скорость роликов:

© -- где й., =

А = а[ =

ь; =

cl =

/-5g-1g (arctg

Yj + VgKPt

(51)

Jc - z Iqs {fi Ri - 22)

Az (fij?oi+f2W . - лгяг/os (f, Rc\ -22)

- \ 1 .

R (Sin po -facospo) +/2г-0 .

P [Sin (Po + }a) - /2 COS (Po + i)] + /г (cos po + fa sin Po + /a-Q COS (a); (Sin p2 -/2 COS Pa) +COS pi;

/os (cos Po -b /2 Sin Po) - R (cos P2 + /2 sin P2) - f2ro sin Pi.

Здесь ©n - начальная угловая скорость роликов в период свободного хода при ©i > © < ©3. Мощность, затрачиваемая на трение,

N,=Az [fiR[d,P+ tnlos {bW + ci8)](©, - ©) +

+ hr, [a-iP - tnlos (b.© + C28) 1 (©2 - ©) 1. (52)

Анализ свободного хода при ©i < © > ©2 показывает, что этому случаю присущи те же зависимости для свободного хода, которые имеют место при ©i :> © > ©2, с той лишь разницей, что тангенциальная сила инерции Р имеет только положительное значение, а формула (49) представляется в виде

= tg (arctg Y 0 + VqsksPt)

(53)

Azmlps (liRbi - frob) . Jc - Azml s (lyRc + firc)

Az (fiRai+f2roa2) Jc-Azmlos if,Rci +(22)

Здесь ©0 - начальная угловая скорбеть роликов в период свободного хода при ©i<©>©2.

Механиз!мы с индивидуальными прижимами. На рис. 5 показана схема сил, действующи на эксцентриковый ролик с индивидуальным прижимом в период свободного хода. Согласно этой

схеме запишем уравнения равновесия в виде суммы проекций на направление, перпендикулярное к ОВ, и суммы моментов относительно центра механизма О:

- yVaSinpo-ZaAaCOSpo + GsinY + Psinp, + + (?cos(a-P sinp + Pcosp = 0; ,

- f.Nro + G/os sin (7 - - Phi 4- Qh + pi = 0.

Совместное решение этих уравнений позволяет определить у Р {hi cos n + h, sin г) - P h, sin p, + Pt {h, cos p, - l s cos ц) / fta (sin Po + /2 cos Po) + f.,ro COS li г

, G [fta sin 7 -/os cos sin (7 - Pi)]

Ih (sinpo-f/2cosp ) + /2rocosn (54)

В течение оборота давление изменяется с изменением угла 7 Чтобы определить величину угла 7, соответствующего минимальному значению нормального уси-ия Л/атш. найдем

= G [{hcosy-

- los<OS (а COS (7 - Pi) = О, откуда 7=я-

-- gl/oscosinp, -tgPx)-

(55)

Из условия контакта роликов 2 mill > о с использованием соотношения (54) найдем величину прижимного усилия, обеспечивающего контакт роликов с обеими обоймами:

Pnhi sin Pi - Pt Ф2 cos Pi - /os COS ц) - P -Gfe Sin 7-<oscosPi Sin (7-Pi)]

fti COS n + Й2 sin n (5o)

Отрыв всех роликов от внутренней обоймы и, следовательно, движение механизма в бесконтактном режиме будет наблюдаться

при Л2 max < 0.

,Угол 7 = 7 , соответствующий максимальному значению усилия Л/гшах. определится аналогично, как и угол 7:

= g(/oscos:sinpr-gpO- (7)

Определив величину Лгтах по уравнению (54) и приравняв ее к нулю, найдем наименьшую угловую скорость наружной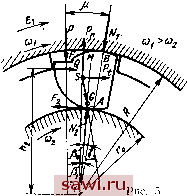

обоймы при бесконтактном движении роликов с внутренней обоймой:

cd? =

Р {hi COS ц -- /i2 sin ц) + Pt (/i2 cos Pj - los cos \i) + + G [fta sin 7 - <oS cos yi sin (7 - Pj)]

mlosfh sin Pi

(58)

ТЕОРИЯ ЗАКЛИНИВАНИЯ РОЛИКОВЫХ МСХ

Усилия, действующие на элементы механизма в период заклинивания и заклиненного состояния. Под заклиниванием роликового МСХ понимают процесс защемления ролика между рабочими

поверхностями обойм в момент такого относительного перемещения их, которое вызывает закатывание ролика в более узкую часть про-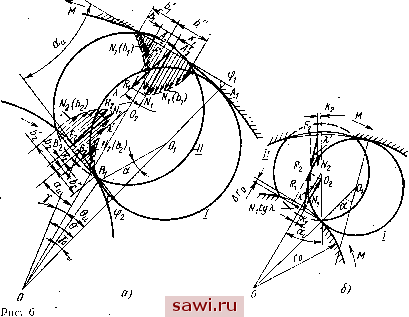

странства между обоймами. Этот период сопровождается приложением, нагрузки к элементам механизма и их деформацией: потерей энергии на трение качения ролика по рабочим поверхностям обойм, потерей энергии на разрыв масляной пленки, гистерезисом и накапливанием потенциальной энергии деформации.

Процессу заклинивания предшествует момент, соответствующий концу свободного хода, когда угловые скорости обоймы Oi и звездочки ©2 становятся равными, т. е. хо = ©г- Заклинивание начинается при ©2 > ©i и заканчивается равновесным заклиненным состоянием.

Если под действием всех сш, приложенных к ролику, в начальный момент процесса заклинивания ролик перемещается