в направлении заклинивания, то произойдет защемление - заклинивание ролика между обоймами. Из уравнения динамического равновесия ролика в начальной фазе его заклинивания получены условия самозаклинивания роликовых МСХ (61).

Механизмы с единичным расположением роликов. На рис. 6, а, б показаны схемы усилий, действующих на ролик, и деформаций основных элементов в процессе заклинивания, что в равной мере соответствует и заклиненному состоянию механизма.

Если в начальный период заклинивания силы инерции, действующие на ролик, и сила прижимного устройства в значительной мере обусловливают силы трения на поверхностях соприкосновения и, следовательно, должны быть учтены при определении условий самозаклинивания, то в последующий период, после того как начнется деформация роликов и обойм, эти усилия весьма невелики по сравнению с усилиями, действующими со стороны обойм. Поэтому при исследовании периода заклинивания и заклиненного состояния ролика между обоймами действием этих усилий пренебрегаем.

Общие реакции и R, действующие на ролик со стороны обойм, вследствие сопротивления при перекатывании ролика смещены от центра площадки смятия на величины и ко, и направлены соответственно под углом Я и Я к линиям действия нормальных усилий.

Условие непробуксовывання механизма в этот период:

Nigl <iVitgPi

я <р1,

где pi - угол трения на поверхности контакта ролика с обоймой.

Предполагая, что нагрузка между роликами распределяется равномерно, запишем уравнение равновесия обоймы

Z {tgk [Z± (r+б)] Tkil

где М - крутящий момент; z - число роликов; / - расстояние между центрами ролика и обоймы; б - суммарная деформация обоймы в месте соприкосновения с роликом.

Величина tg Яб ki весьма незначительная, и ею можно пренебречь, тогда

г (I ± г) tg \

Нормальное давление и угол Я определяются, если записать уравнения равновесия ролика Ni .- (60)

cos?. COS я,

Из рис. 6 видно, что сс я + Я.

Используя формулы (59), (60), (62), найдем

М COS (Си -- Х) - г (1±г) sin X

(61) (62)

(63)

Необходимо заметить, что Я>Г, следовательно, а > i-Приближенно нормальные давления найдем из формул (59)

и (63), если принять Я=-у-:

,(64)

На основании формул (60), (61), (62) получим

, /-sin a + k, + kcos h (65)

~ /-(1-t-cosa ) -Й2 sin я ,

Считая, что нормальные давления по длине ролика распре- делены равномерно, в соответствии с обозначениями на рис. Ь запишем

lp[NAb)db,; N2l,[NAh)db, (66)

bl h

= /p ( b,N, (&i) db,; NA = p 1 b.No (b,) db.

(67)

После подстановки значений и из выражения (66) в формулу (67) получим

bN (6,) dfti

-; h =

bN-, (Ьг) db

2 (62) db.

или после интегрирования

kx==kx{b[ b\); Й2 = h \Ь<г + б,).

Так как величина Ь\ + Ь\ равна ширине площадки контакта Ь ролика и наружной обоймы, а &2 + 62 равна ширине площадки контакта 2 ролика и звездочки, то можно записать

Здесь Pi и Рг ~ коэффициенты меньше единицы определяющие долю смещения усилия N\ и от середины площадки смятия. Приближенно с некоторым запасом можно принять Pi = Р2 = = 0,25.

Величины b1 и bl определятся:

&2 = 2,15Т/4±

где El, £2 и Ер - модули нормальной упругости материала поверхностных слоев наружной и внутренней обойм и ролика;

- радиус кривизны профилирующей кривой звездочки в средней точке контакта; /р длина ролика.

Если принять во внимание, что у большинства механизмов, нашедших применение в технике, основные звенья выполняются закаленными с высокой твердостью, то величиной sina в силу ее малости можно пренебречь, тогда формула (65) примет вид

ia 1 - ia \ l.+ 2 COS

Г (K+cosa ) При ki = 2 = k получим

tg X = tg

(68)

В этом случае для механизмов, основные звенья которых выполнены из одинаковых материалов, принимая во внимание формулу (59), найдем

k з.озр У

Mr zlpEl Щк-

После подстановки значения k из последнего выражения в формулу (68) и соответствующих преобразований запишем

tg Я - 2 tg tg X + tg tg isPW

zlpErl

- = 0.

Решая это кубическое уравнение в тригонометрической форме,

осуществив подстановку tg = л: 1 4-C0S

tgA=4tg

arccos

tga , получим

123,9зрш

ZlpErl tg 3L

(69)

Из анализа последнего выражения следует, что с уменьшением радиуса ролика г увеличивается угол К, поэтому при проектировании с целью соблюдения условия заклинивания необходимо выбирать диаметр ролика по возможности большим. Однако при этом следует учесть, что для быстроходных механизмов увеличение диаметра ролика не всегда будет оправдано, ибо это мойсет привести к увеличению динамических усилий, которые в значительной мере влияют на увеличение потерь в период свободного хода.

Механизмы с эксцен- триковыми роликами. Уравнение равновесия ролика (рис. 7):

Ni N, .

C0S(\J-t-1)

COS (ф + V)

Sin (ij) + V) siii (Ф -f v)

(70) Рис.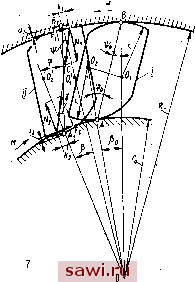

где Ф и t5 - углы давления в процессе заклинивания механизма. Так как

Ф = <1з + Р, то

И, следовательно, условие заклинивания механизма запишется

tg (Ф + Y) < N2 tg Р2 или.

Ф <>2 - Y.

где р2 - угол трения на поверхности контакта ролика и внутренней обоймы в процессе заклинивания.

. Без учета смещения реакций нормального давления при перекатывании ролика, т. е. при = 2 = о, и, следовательно, при y = о условие заклинивания запишется так:

Ф <Р2. (71)

Анализ процесса заклинивания указывает на то, что угол го соответствует половине угла заклинивания для роликовых механизмов с цилиндрическими роликами.

Из уравнений равновесия обойм имеем

- - - лЛ + 1 tg ( + y) = 0;

- л2Й2- Лf2tg(ф + y)o = 0,

и далее найдем

iV2 =

zKtg (ф + 7) + А2]

или, принимая kj = k о,

будем иметь м

(72) (73)

л1 =

л2 =

(74) (75)

гго tg (р

Рассматривая положение ролика в период заклинивания (см. рис. 7, положение ), найдем

но так как ф < ф < 4°, то можно принять sin гз tg ф, тогда

tg ф и sin ф :

M(R-\-u)

zR (го - u-i) sin ф М

(76) (77)

zro sin ф

На основании уравнений (70), (72) и (73) найдем угол y. при этом в силу малости этого угла будем считать cos y 1 и sin y y-

Гр sin ф - . sin -- cos тр + cos ф COS ij) - Го COS ф -j- sin \) + 2 sin ф (78)

Используя выражение (37), найдём угол ф:

Ф = arcsm

jR + ro + Ui-uf-e- 2{R-r-\-Ui)(ro-\-r - 2)

(R + + (fo - Uif -2{R + Ui) (Го - 2) X - (R + ro + Ui-U2)-e , . 2(?-r-Ui)(ro-f r- 2)

(79)

Из анализа формулы (79) видно, что у этих механизмов с увеличением нагрузки угол ф увеличивается, что приводит к увеличению вероятности проскальзывания обоймы в процессе заклинивания.

Угол

ф = arcsin

Tq - Uz

R + иг J

(80)

Величину общей деформации 1 в месте контакта ролика с наружной обоймой и величину сближения в месте контакта ролика с внутренней обоймой определим на основании формул для сближения цилиндрических тел, приведенных в работе 161 ], а также формулы для определения деформации кольца, нагруженного радиальными нагрузками. При этом будем считать что обоймы и ролики выполнены из одного материала. Сближение цилиндров

1 -Ь m + 2m

(81)

где q - интенсивность нормальной нагрузки по длине ролика; Е - модуль нормальной упругости; т - коэффициент Пуассона; Ri и /?2 - радиусы цилиндрических тел.

Деформация кольца в месте приложения нагрузки [61 ]

qipR

Sin

360° -

(82)

где / - длина ролика; J - момент инерции сечения кольца.

Используя формулы (76), (81), (82), определим Mj и и: М/?(л1пА. + р)

(Го - 2) Sin Ф - 7И ( >1 In А. + Di)

М2 = -(Л1пА. D2). .

2 sin ф \ М I

(83)

(84) 185