Здесь

2(1 rn) ..... 2(l-m) .

2 (I -m - 2trfi).

, 2пЕг1рГо {R - r) sin фр . , гяг/рГо (о + r) sin фо .

i- fzrj 2---:г7Р-

2(1 OT -2m) пЕг1рГо

Так как различие в углах ф и фц относительно невелико, то при выводе формул (83) и (84) под знак логарифма в выражение (81) вошла величина интенсивности нагрузки, определенная по формуле

9 = г/р.о 1дф (85)

Относительное перемещение роликов в процессе заклинивания.

В процессе заклинивания по мере деформации основных элементов механизма ролик перекатывается по рабочим поверхностям обойм, устремляясь в более узкую часть пространства между ними.

Пусть при действии на механизм момента М (рис. 8, а, б) ролик из положения / переместится в положение аобойма повернется на угол относительно звездочки. Обозначим полярные координаты центра ролика Рц и бц. Поместимшолюс в центре механизма в точке О, а полярную ось направим по линии 00о-Сувеличением крутящего момента на величину dM ролик переместится в положение /, совершив элементарное движение, а обойма повернется относительно звездочки на угол d. При этом, очевидно,

= ttdMi. (86)

После интегрирования получим

Рц = / 1. (87)

Для определения угла 0ц рассмотрим положения и / (на рис. 8) ролика в процессе заклинивания. Из треугольников Оффч и ОВВ находим ....... .

--=±/-р(вд) + 1;

± - Р (вд)

cos аи

г - 2 - d 2

создай -f d<xy, 186

d [р (вц)] + 1 dUi

(88) (89)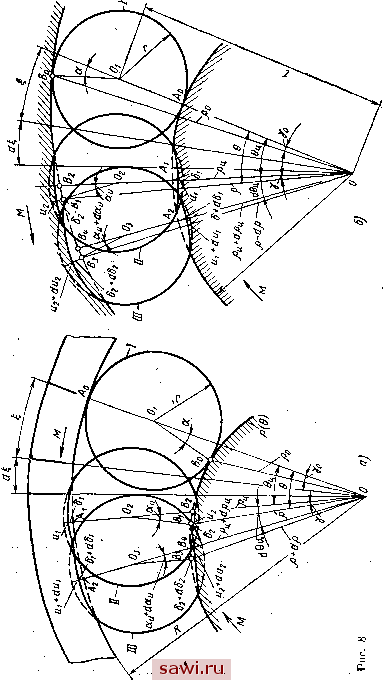

Если принять cos а cos (а + daj, то, вычитая почленно из уравнения (89) выражение (88), получим

[р(9ц)] == (dMi + dMa). (90)

Уравнение (90) получено в предположении, что участки направляющей кривой рабочей поверхности звездочки БВа и прямолинейны. Это предположение достаточно обосновано, если учесть, что а <: 10°, а кривизна направляющих кривых относительно невелика.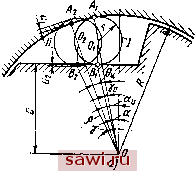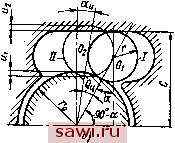

Рис. 9

Интегрируя уравнение (90), получим Р (0ц) = Ро ~ ( 1 + а)- (91)

Уравнение (91) является исходным при определении угла 9. Используя это уравнение, определим зависимость между углом 0 и моментом М для наиболее распространенных на1Ч)авляющих кривых контактных поверхностей звездочки.

Величина р(6ц) и рц для плоской контактной поверхности найдется из рассмотрения рис. 9 , а, б: с . с

Р(вц)-

COS (а ± бц) И, следовательно,

с cos а

Ро =

cos та

(92)

вц =: arccos

с ± ( 1 + Ua) cos а ,

где с - расстояние от центра звездочки до рабочей поверхности.

Для цилиндрической контактной поверхности с направляющей кривой в виде логарифмической спирали р = ев* запишем р (ej = e(o-Vo+B) ctg 1= и e(e -v ) ctg г,

или, подставляя в уравнение (91), получим

Ui + Uj

e, = tgi;ln

(93)

где \1р - постоянный угол между касательной и ради усом-вектором.

Значение угла

п г> г, i if sin а 9o==2.3tgiplg[3)

Угол

г sin а

Yo = arcsm

V{1 ± /-)2+2r(l +cosa) / или

Yo = 90° a).

Для цилиндрической контактной поверхности звездочки с направляющей кривой в виде спирали Архимеда с началом координат в точке О и полярной осью, направленной по OAq, получим

р (8ц) = а {2м1 ± й) и ро = 2апп,

где rt - число витков спирали Архимеда, равное О, 1, 2, 3, ... После подстановки значений р (0) и ро в.выражение (91) найдем

(94)

Для цилиндрической контактной поверхности звездочки в виде круглого цилиндра, очерченного радиусом Го = / - / из центра

с эксцентриситетом е = 2/sin величина () (вц) определяется:

р (0 ) = 21 Sin - Sin (-J ± 0д) + Y{l+rf-U sitf -f-cos ± 0ц).

В силу малости угла 0ц принимаем cos 0ц Тогда

гдеГо=/ + г; = 2/sin*--; fo = /sina.

1 и sin 0ц

(95)

Таким образом, относительное / движение центра ролика, в зависимости от нагрузки, в процессе заклинивания определяется в полярных координатах в параметрической форме уравнениями (87) и (92)-(95).

Относительное перемещение обойм в процессе заклийивания. При заклинивании обоймы под действием нагрузки вследствие деформации как самих обойм, так и роликов поворачиваются в относительном движении на угол . Этот угол является одной из главных характеристик МСХ. Его большое прикладное значение состоит в том, что он опреде:яет падение углового перемещения и угловой скорости ведомого звена механизма; существенно

влияет на величину минимального угла размаха ведущего звена, при котором механизм начинает функционировать; в значительной мере определяет потери в процессе заклинивания и усилия, действующие на звенья механизма. Он является главным фактором при определении дуги перекатывания ролика, по контактной поверхности звездочки в процессе заклинивания. Эта дуга не должна превышать длину профильной линии рабочей поверхности звездочки, иначе механизм не будетработать.

Чтобы определить зависимость угла I относительно поворота обойм от момента М, действующего на механизм, рассмотрим схему перемещения роликов и обойм в процессе заклинивания (см. рис. 8). В период заклинивания по мере деформации основных элементов МСХ ролики перекатываются с проскальзыванием по рабочим поверхностям обоймы и звездочки, перемещаясь в сужающуюся часть клинового пространства между ними. Элементарное движение ролика из положения в положение / осуществляется подобно перекатыванию сателлита в фрикционной дифференциальной передаче при наличии проскальзывания ролика в местах контакта с обоймами и деформации как ролика, так и обойм. Приближенно без учета проскальзывания ролика величину dl можно определить так:

dl==de+dQ,

(96)

где 6ц - угол поворота центра ролика; рр и Rp ~ средние радиусы рабочей поверхности звездочки и обоймы с учетом их деформации при перекатывании ролика из положения в положение /.

Обозначив деформации обоймы и -звеадочки в местах контакта с роликом 6i и бз (см. рис. 8), определим

Рср КР + 62) + (Р ± Ф + 83

ад = р i- 62

i?ep = [( ± /- ± 61) + (/ ± г ± 61 ± d8i)] = / ± г ± бд ±

Тогда уравнение (96) можно записать в виде

2 d6i

didQ +

Р -1- 62 ±

I ± г ± 81 ±

Пренебрегая бесконечно малыми величинами второго порядка и величинами б и 63 как весьма малыми по сравнению с и г, после интегрирования последнего уравнения будем иметь

1 = 0ц. 190

/ ± г

Р0ц.

(97)

Это уравнение является исходным при определении угла для механизьТОв с различными контактными поверхностями.

Плоская контактная поверхность. Для плоской контактной поверхности-Звездочки (см. рис. 9)

(98)

cos (а ± 7о ± бц) при этом считаем, что угол у = уо. затем по формуле (97) находим

1 = еи + 7Ь

cos (а ± 7о ± бц) tg

(а±7о ±-6)+-

Подставляя 6ц из уравнения (92), получим

1±г ± arccos

Intg

arccos

с cos а

с cos а

с ( 1 + 2) cos а - 2 с / а ± 7о

с ± ( 1 + 2) cos а J I ± г

lntg(

я \

Цилиндрическая контактная поверхность с направляющеТйв виде лога(рифми-ческойспирали. Если на рис. 8 профилирующая кривая представляет логарифмическую спираль в полярных координатах с полюсом в центре механизма - точке О, то

p=e(W)<=**. .

Уравнение (97) можно записать так:

=вц+-

±г

Используя уравнение (93), получим

i = tgln

1 + 2

- (9o-Yo)ctgt

к ±

J ±г

(99)

(100)