Цилиндрическая контактная поверхность с направляющей в виде спирали Архимеда. Используя формулу (18) гл. 12, на основании рис. 8 получим

р = а(2ли :i Yo =t Эц).

Угол I, согласно уравнению (97), 0.

= 9 + Т

± г

fl(2nrt±Yo + ejde

1 +7-(2ля ± Yo)

4{l±r)

Подставляя . 9ц из формулы (95), Ьудем иметь

? = + а

1 + ± То)

- 2(/ ± г)а

(101)

Круглая цилиндрическая контактная поверхность. Уравнение окружности контактцой поверхности звездочки с радиусом и эксцентриситетом / ъ полярных координатах р, 9 с началом координат в точке О (см. рис. 8) и полярной осью, направленной-по ОА:

. p = aiSln(±Yo±e ) + fe/l -4cos( ±Vo± вц).

Для определения угла g подставляем в уравнение (97) найденное значение р. Тогда

I = 0,/+ y7 I sin (-- ± Yo ± вц) йЭц +

о .

+ ?/1-#соз(1-То=.вц) 0д-

Второй интеграл этого выражения приводится к эллиптическому интегралу 2-го рода, если осуществить подстановку

я а

-2 - Ф = ± То ± Од-

Действительно, а,

? = 0ц +

/ ± т

/ ± г

;cos(:Yo)-cos(±Yo±Oц) -/ 1 -.зшфйф.

Y - Y Т v

Окончательно запишем = 9д + 77 [°Кт- - Vo) - cos (4 ± То ± ej] +

Vo)-(f.l-l-To-e )].

(102)

Механизмы с эксцентриковыми р ол и -к а м и. Следуя работе [143], получена приближенная формула по определению угла \ для МСХ с эксцентриковыми роликами.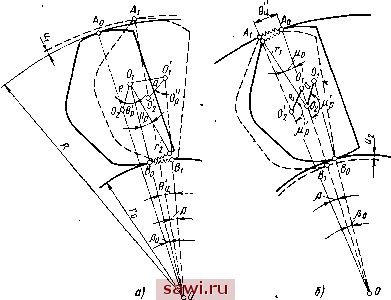

Рис. 10

Угол относительного поворота обойм при ааклинивании найдем как сумму углов; угла поворота наружной обоймы относительно неподвижной внутренней обоймы вследствие деформации в месте контакта роликов с наружной обоймой (рис. 10, а) и угла \ поворота внутренней обоймы относительно неподвижной наружной обоймы с учетом деформации в месте контакта роликов с внутренней обоймой (рис. 10, б), т. ё.,

I = i + 1в.

Угол определим как угол поворота наружного кольца для планетарного механизма при неподвижном внутреннем элементе:

Тогда угол поворота наружной обоймы

Г2 (R+ro + Ui)ep

Из схемы (см. рис. 10, а) перекатывания ролика видно, что ООдоГи 00102? определятся из рассмотрения треугольников

cos Эр =

Р--2е(го+г,)-

Рассматривая перекатывание ролика по неподвижной наружной обойме без скольжения при наличии деформации в-месте контакта ролика и внутренней обоймы (см. рис. 10, б) и используя соотношения, определяющие перемещения звеньев планетарных механизмов, найдем угол поворота внутренней обоймы:

Величина

Тогда можно записать

? - 1 + 0 - Uj) Хр

Riro-u,)

Центральный угол, стягивающий дугу перекатывания ролика, fip = jip - iip.

В соответствии со схемой на рис. 10, б

fP---2e(R-ri)-

COSfXp=-2e(R-ri)-

Все составляющие известны для определения угла относительно поворота обойм, и можно записать формулу в окончательном виде:

r2{R+ro+Ui)Qp ri{R+ro-U2)y.p

Го {R + Ul)

R(ro-U2)

(103)

Так как /? > i и Гц > Ыз. то приближенно величина угла будет

g--l-A+-iFp)-

(104)

ДИНАМИЧЕСКИЕ НАГРУЗКИ, ДЕЙСТВУЮЩИЕ НА МСХ,

И ПРОДОЛЖИТЕЛЬНОСТЬ ДВИЖЕНИЯ В ПЕРИОД ЗАКЛИНИВАНИЯ

Уравнение относительного движения обойм. У импульсных вариаторов процесс заклинивания протекает за весьма небольшой промежуток времени при . действии динамических нагрузок. Вопрос о влиянии динамических нагрузок на прочность и долговечность МСХ и о величине этих нагрузок в период заклинивания мало изучен, поэтому неслучайно, что ряд МСХ импульсных

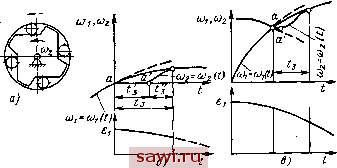Рис. 11

вариаторов показывает недостаточную выносливость. Расчетная схема при определении динамических усилий на МСХ показана на рис. 11, а.

Если не учитывать высокочастотные колебания обойм, то процесс заклинивания можно представить так. После момента, соответствующего концу свободного хода, когда угловые скорости наружной (Oj и внутренней а2 обойм уравниваются (точка а на рис. 11, е), начинается относительное движение обойм под действием приложенных к ним внешних сил, при котором ролики заклиниваются в пространстве между обоймами. В результате деформации роликов и обойм*в процессе заклинивания ведущая обойма поворачивается относительно ведомой в направлении дви-

7* 195

жения, при этом угловая скорость са несколько превышает угловую, скорость ©г (участок аЬ). Так как в течение всего периода заклинивания разность ©j - ©2 остается положительной, то, очевидно, в этот период имеет место непрерывное увеличение деформаций деталей механизма и, следовательно, непрерывное нарастание относительного угла поворота обойм g. Рассматриваемый период заканчивается равновесным заклиненным состоянием, при котором опять ©1 = ©2 (точка b на рис. 11, б).

Штриховыми линиями на схеме показаны изменения угловых скоростей обойм, если бы не произошло заклинивание. Характерно, что в начальный момент заклинивания относительное угловое ускорение обойм е = -е, имеет положительное значение, затем в процессе заклинивания изменяет знак и в конце периода заклинивания становится равным нулю. Период заклинивания продолжается, пока имеет место увеличение суммы моментов сил сопротивления и сил инерции, приложенных к ведомой обойме механизма. Если эта сумма, достигнув своего максимума, в конце заклинивания остается постоянной, то в дальнейшем обоймы будут совершать движение с одинаковой скоростью иначе будет происходить относительное угловое, смещение обойм. Последний случай характерен для быстроходных МСХ; особенно для тех, обоймы которых движутся при неустановившихся режимах.

В период заклинивания на ведущую обойму кроме момента сил движущих Мд и сил сопротивления действует момент М (I) со стороны ведомой обоймы, изменяющийся в зависимости от угла I. На ведомую обойму в-этот период кроме момента сил сопротивления Мс действует такой же момент М () со стороны ведущей обоймы, направленный по ходу движения. Зависимость М = М (g). будем называть характеристикой жесткости МСХ.

Уравнения движения обойм при заклинивании:

для ведущей обоймы

d (JfL.) = [Мд - м; - м (I)] diu

для ведомой обоймы d{-) = [M{l)-M:]db,

(105)

(106)

где 1 и I2 - углы поворота ведущей и ведомой обойм в период заклинивания; и /2 - приведенные моменты инерции ведущей и ведомой систем.

Величины и /2 могут быть выражены в функции от угла поворота звена приведения.. Однако относительно малая продолжительность периода заклинивания в большинстве случаев на практике позволяет принять приведенные моменты инерции J

И постоянными. Тогда на основании уравнении (105) и (106) можно записать П, ] [М-Мс-М{1)];

(107) (108)

л2 ~

-=J-[m(E)~m;].

Так как относительная угловая скорость обойм в период заклинивания равна разности угловых скоростей © = и,-©g, то относительное угловое ускорение

(109)

дельного движения обойм в общем виде

где J -

(110)

Функциональную зависимость изменения момента М () можно определить теоретически при допущении, что в процессе заклинивания ролики перекатываются по рабочим поверхностям обойм без проскальзывания (см. стр. 190) или на основании экспериментов. Так как характеристики жесткости МСХ представляют монотонно возрастающие функции [44, 611, то их аппроксимируем кривыми вида

М = Л*. (111)

Для определения величин А м h прологарифмируем выражение (111):

lgM = lgЛ+61g£ (112)

и построим (рис. 12) по экспериментальным данным прямые в логарифмической системе координат согласно уравнению (112). Кроме прямых на рис. 12 построены кривые М = М () в обычной системе координат. Точки без существенных отклонений укладываются на прямых линиях, что указывает на хорошее совпадение аппроксимирующих кривых с опытными.

Если принять зависимость М = М () согласно уравнению (111), то дифференциальное уравнение относительного движения обойм при заклинивании запишется так:

d Л. Mgft-

(из) 197