образующего механизма (рычажного либо кулачково-рычажного) преобразуется в колебательное движение ведущего звена МСХ. Угол поворота фг. ведущего звена МСХ может быть выражен периодической функцией угла поворота Ф (Ф1) вала электродвигателя. Машинный агрегат с МСХ с целью удобства исследования

можно разделить на две части: ведущую систему, включающую цепь от приводного двигателя до МСХ, и ведомую - от МСХ до исполнительного органа.

Обычно упругий момент системы с МСХ выражается М = = [61], где I - угол относительного поворота приведенных масс, связанных с обоймами МСХ; А - коэффициент, характери-

зующий податливость МСХ и других упругих элементов системы; Ъ - показатель степени, определяющийся эмпирически, 1 < b <2.

Считая приведенные моменты инерции ведущей 1 и ведомой /2 систем постоянными, движение звеньев машинного агрегата с колеблющимся ведущим звеном МСХ, если пренебречь демпфированием, будет описываться следующей системой нелинейных дифференциальных уравнений:

Ф1 \Н + \h [Ф (ф1)]} (ф1) + Ф?/2Ф(Ф1) Ф (ф1) ==

= Мд-М,Ф(ф1); (1)

- Ф1ЛФ(Ф1) rih - фФ (фО + == Л4с, (2)

где I = ф2 -ф; ф -угол поворота ведомого звена МСХ; =

= ; Ф (Ф1) = ,2** ; Мд и М(, - движущий момент

и момент сил сопротивления; - функция, учитывающая односторонность упругой связи МСХ, которая определяется при упругой характеристике: по рис. 1, а

1 при О

>0

по рис. 1, б

[1 при I > б,

1 =

где б - угол, на который поворачиваются обоймы МСХ в относительном движении с момента равенства их угловых скоростей до момента начала заклинивания МСХ.

Для данной системы нелинейных дифференциальных уравне-. НИИ можно найти приближенные решения, позволяющие в общем виде выявить влияние различных параметров машинного агрегата на величину динамических нагрузок, возникающих при заклинивании МСХ. Для получения приближенных решений воспользуемся методом последовательных приближений при интегрировании по участкам.

Разрешим систему дифференциальных уравнений (1) и (2) относительно вторых производных ф1 и \:

;=-Ф(ф1) + - + Ф(ф1)--{/1 + Л[Ф(Ф1)П- (6)

Будем рассматривать наиболее общий случай, считая Мд = == Мд (фх), М(, = М(, (ф, ф, t). Но так как ф = Ф (Ф1) - , Ф = фдФЧфх) - то момент сил сопротивления

Ме==млФ(Ф1), Фы, cpiin.

Разобьем рабочий цикл прообразующего механизма на участки. Представим нелинейные функции правых частей уравнений

(5) и (б) в виде рядов Тейлора и, учитывая малость рассматриваемых участков, ограничимся квадратичными членами рядов

Мд = 1-}-+ ;

лд ы ф(фо = bi + + Ьз7 + ; Me = + d2V + dsP

Ф?Ф (Ф1) = gi + g2Y + g3Y + ; . (7)

l . = 1 + 2p + зР; ?*ф{ф1) = /1 + /27+/зР + -;

МФ(ф1)1= = 51 + 527 + 5зР+...,

где V = Ф1 - Фо; i = ч> - Фо; Р= ? - ?о; Р = I - 4; Фо.

Фо> ?о. to - значения ф, ф, I, \ в начале рассматриваемого участка; а, d,-, f,-, g, k, s,- - коэффициенты разложений соответствующих функций в ряды Тейлора, i = 1, 2, 3, ... В первом приближении примем

% = W. Ро= Ро-

Тогда, заменяя нелинейные функции в правой части уравнений (5) и (6) выражениями (7) и подставляя в них порождающие решения (8) после интегрирования, получим вторые приближения решений:

Ф1(0 = Ф10+ W +

; (О = lo+й + -yif+-yt+-

2з*;

(9) (10)

где i/i, г/2, /з, 2i, 22, 2з - постоянные, которые получаются группировкой при одинаковых степенях t коэффициентов разложений (7) правой части уравнений (5) и (6) с подставленными в них порождающими решениями (8).

Для машинных агрегатов с малой частотой включений МСХ время рабочего цикла обычно составляет десятые доли секунды. Для агрегатов со средней и большей частотами включений МСХ время рабочего цикла уменьшается до сотых либо тысячных до/ лей секунды. При делении рабочего цикла на участки шаг интегрирования будет составлять тысячные доли секунды. Поэтому в выражениях (9) и (10) членами, содержащими и t, в большинстве случаев для практических расчетов можно пренебречь.

Заменяя коэффициенты а,-, 6 d,-, s,- рядов (7) их йстийнымй значениями и пренебрегая членами с f и после преобразований, решения (9) и (10) .запишем

- + ФшФо-

Л* [л-Ь/2 (Фо)2]

Ф1 (0=Ф10+Ф-

f, . (12)

где Мдо и Мсо - значения Мд и Мс в начале рассматриваемого участка; Фо и Фо - значения Ф(ф) и Ф (ф) в начале рассматриваемого участка.

Угловая скорость относительного поворота обойм МСХ равна

;(0 = io + s,

В = фоФо

(13).

(14)

В начале рабочего цикла Ф(ф1) возрастает и ФЧфх) > О- На участке убывания Ф(ф1) - функция Ф (ф1) < 0. Для агрегатов со средней и высокой частотой включений МСХ, у которых угловая

скорость ф1 ведущего звена велика, на участках, где Ф (ф) имеет наибольшие значения, член фоФо в выражении (14) становится на один-два порядка больше члена, содержащего Мдо й Мсо- При этом происходит резкое возрастание вследствие кинематического возмущения фФо, поэтому в дальнейшем значительно возрастает. . Следовательно, для агрегатов, особенно с частыми включениями МСХ, динамические нагрузки от кинематического возмущения могут в несколько раз превышать нагрузки от силового возмущения. По мере роста \ член, содержащий Л * в выражении (14), будет увеличиваться и величина В начнет уменьшаться. Функция t {t) = max, когда I (t) = О, т. е. при В < 0. Так как упругий момент равен М {t) = А l{t), то динамические нагрузки зависят от жесткости МСХ, степени Ь. Как видно из выражения (14), при уменьшении Ji либо члены, содержащие в знаменателе /1/3, будут расти. Однако член, содержащий Л*, как показали вычисления, на один-два порядка больше члена, имеющего Мдо и Мсо- Поэтому снижение величины либо /3 приводит к уменьшению динамических нагрузок на МСХ.

При установке упругого звена либо муфты, связывающей ведомую обойму МСХ с ведомой системой, момент инерции маховых масс, непосредственно связанных с ведомой обоймой МСХ, Jb Ji> и это приводит к снижению динамических нагрузок при заклинивании. В этом случае в выражения (И) и (14) вместо Мо и /3 следует соответственно подставлять М(,о = Мз (фо), J2 = где Ма {) - упругий момент муфты; - угол отно-

сительного поворота полумуфт; % - значение ф в начале рассма триваемого участка.

Установка упругой муфты на ведущем валу преобразующего механизма также приводит к снижению упругого момента на МСХ, и в выражениях (11) и (14) следует заменить Мо = ( о). 1 = где Ml (а) - упругий момент муфты; а - угол относительного поворота полумуфт; а - значение а в начале рассматриваемого участка; Jm - момент инерции ведущего звена преобразующего механизма и связанных с ним элементов.

Так как в период установившегося режима работы агрегата угловая скорость ц>1 ведущего звена преобразующего механизма незначительно колеблется относительно постоянной составляющей фср, то для практических расчетов в некоторых случаях на всем участке рабочего цикла в выражении (11) можно принять Фю = const!

Если функция ФХфО имеет скачок , то при интегрировании сразу после скачка целесообразно уменьшить шаг интегрирования для увеличения точности. Если функции М, либо Ф (ф1) имеют излом , т. е. их производные имеют скачок , то в решения? (9) и (10) следует сохранить члены, содержащие t. Зная = = I {t), можно определить предельное число циклов включения МСХ. Если на протяжении рабочего цикла > О, то расклинивания МСХ не происходит. Отсюда можно сделать вывод, что максимальное число циклов включений, при котором МСХ функционирует нормально (т. е. происходит заклинивание и расклинивание), можно находить при условии периодического изменения I {t) с переходам через нуль.

Машинные агрегаты с вращающимися звеньями МСХ. Расчет-аая схема машинного агрегата при использовании динамической характеристики электродвигателя показана на рис. 3, а и статической - на рис. 3, б, где ведущая и ведомая системы имеют приведенные массы 1 я 2 с моментами инерции я Ja, между которыми установлен МСХ.

Если характеристика приводйого электродвигателя задана в виде [20]

nMд+ Mд-f Wva)o = 4-, (15)

то движение звеньев машинного агрегата с МСХ будет.описываться системой нелинейных дифференциальных уравнений

VCOo

UiAl --

М. = 0;

ЛЛ + (Л + Л) [ i i -f 2 (1 - 2)] i + + (Ji + Л). И?* - /аМд - = О,

где I = ф1 - ф2; ф1. ф2 - углы поворота масс 1 я 2 я связанных с ними обойм МСХ; М. - момент сил сопротивления; п/- коэффициент затухания колебаний для МСХ, находящегося в заклиненном состоянии; - коэффициент затухания колебаний в период свободного хода МСХ; - электромагнитная постоянная времени; v - крутизна статической характеристики электродвигателя; соо - синхронная частота вращения вала электродвигателя.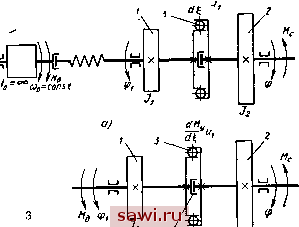

Рис.

Коэффициент затухания колебаний для МСХ, находящегося в заклиненном состоянии, легко определить экспериментально через логарифмический декремент затухания.

При решении системы (16) могут возникнуть две задачи: определение наибольших динамических нагрузок на МСХ при заклинивании и нахождение периодических решений в случае периодических возмущений моментов.

Первая задача рассмотрена в работе [61 ] и может быть решена методом кусочно-линейной аппроксимации и припасовывания решений. Во втором случае, представляя момент сил сопротивления в виде

Мс = Мц + Ма sin со

и учитывая несимметричность упругой характеристики МСХ и наличие демпфирования, периодические решения системы (16) в первом приближении примем

i = о + 1 sin ©Г+ 2 cos Ы\М, =.Ьо + bi sin со + - + bo cos со.