. Коэффициенты flo, fli, fla, bg, bi, ba. следуя методу Галеркина либо Ритца [56], [58], определяют из системы уравнений

J Fx (Мд, 1)Ут atdiO; \ F (Мд) sin at dt = 0; о о

т т

>1(Мд, )со8сйЫ = 0; \F2{Ml)coswtdt = Q, (18)

. о б ,

где Т = Fx (Мд, ?) и Pj (Мд, ?) - левые части соответственно

первого и второго уравнений системы (16), в которых вместо Мд I I подставлены их значения, определяемые выражениями (17).

При рассмотрении стационарных режимов работы агрегатов с большой частотой циклов включения МСХ, когда колебания системы будут происходить за зоной эле]тромагнитного резонанса, можно воспользоваться статической характеристикой электродвигателя [т. е. принимая в выражении (15) Та = 0], и тогда относительное движение обойм МСХ будет описываться следующим нелинейным дифференциальным уравнением:

[ itii-i- 2(l - l)]l

UxAV +

+ -7-7 [ i i+ 2(1- i)]l -W- uxAi = , + 4

(19)

При условии- постоянства движущего момента Мд = const относительное движение обойм запишется

J1+J2

[ад+ 2(1 -Ux)\\

J1+J2

JyJ.

Мд . , Мс

г г

1

(20)

В первом приближении периодическое решение уравнений (19) и (20) примем в виде первого выражения (17).

Коэффициенты Ug, fli, легко найти по методу Галеркина. Так как в выражениях для определения коэффициентов Од, fli, fl2 имеются члены в степени Ь, величина которых для реальных систем дробная, то проинтегрировать эти уравнения в общем виде не представляется возможным.

Используя выражения для коэффициентов . j, fla, можно построить амплитудно-частотную характеристику и, составив

уравйеИия в вариацийх, йсследоВатЬ известными Методами [58] устойчивость стационарных режимов работы машинного агрегата с МСХ.

Для МСХ большой грузоподъемности с большим числом роликов при достаточно жестких валопроводах ведущей и ведомой систем агрегата можно принять b = 1, и тргда уравнения (18) после интегрирования будут определяться известными выражениями [21 ].

Используя метод Галеркина, можно найти вторде и третье приближения. Нахождение решений в первом приближении позволяет получить качественно правильные результаты и вместе с тем значительно уменьшить объем вычислений.

Глава 8

ДИНАМИКА

ПЛАНЕТАРНЫХ ВАРИАТОРОВ

Период заклинивания. Возможны два случая начала заклинивания: при наличии выбега ведомой системы вариатора и без выбега

При отсутствии выбега в процессе заклинивания происходит перераспределение нагрузки между МСХ, заканчивающим передачу энергии, и смежным МСХ, вступающим в работу; первый постепенно освобождается от нагрузки, а второй постепенно нагружается.

Явление перераспределения нагрузки между смежными преобразующими механизмами и МСХ можно представить так: в начале периода ведущий нагружен больше, чем вступающий в работу, затем наступает момент, когда оба МСХ нагружены одинаково и в конечной стадии первый освобождается от нагрузки по мере того как второй ее воспринимает.

При наличии выбега все МСХ, в том числе и смежные, к началу заклинивания совершают свободный ход. Поэтому в процессе заклинивания участвует только один МСХ, и если выбег непродолжительный, то такое включение МСХ может оказаться при действии .больших усилий, чем в случае без выбега.

При динамическом анализе планетарного импульсного вариатора учитываем жесткость наиболее податливого узла в системе привода - МСХ [10]. Так как упругий момент на МрХ обычно достигает наибольших значений в первый полупериод колебаний, за время которого демпфирование не успевает оказать существенного влияния на формирование упругого момента, то демпфированием в МСХ пренебрегаем.

Планетарные импульсные вариаторы обладают наиболее сложной динамикой, все остальные системы импульсных вариаторов в смысле динамики движения с учетом податливости МСХ и перераспределения нагрузки между ними в процессе заклинивания представляют частные случаи. Поэтому ниже изложенный динамический анализ в значительной мере можно распространить и на непланетарные системы импульсных передач.

Расчетная схема вариатора показана на рис. 1. Для получения дифференциальных уравнений, описывающих движение звеньев вариатора при заклинивании МСХ с учетом податливости последних при фиксированном передаточном отношении, воспользуемся уравнением Лагранжа 2-го рода, выбрав в качестве обобщенных координат углы поворота ведущего звена - водила и фа ведомого звена МСХ относительно водила.

-Пренебрегая кинетической энергией ведущих звеньев МСХ в их вращательном движении относительно центра масс как ма-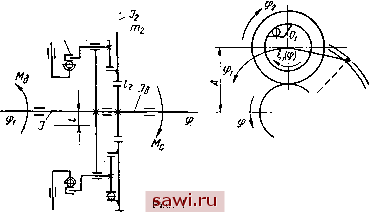

лыми величинами, а также считая, что пазовый диск вращается QOBMeCTHO с водилом, определим кинетическую энергию вариатора;

2T=[J. + h (Ф1 -

Jkaw{m3

то)] ф1 -f kJo (ф1 =f: ф2) -f

где / -момент инерции водила и связанных с ним ведущих элементов; - момент инерции ведомой системы вариатора; > Jq - моменты инерции пазового диска и ведомой обоймы МСХ относительно его оси; т, т - массы соответственно ведущей и ведомой обойм-МСХ; k - число преобразующих механизмов; - межцентровое расстояние зубчатой передачи; i - передаточное отношение зубчатой передачи при неподвижном водиле.

Здесь верхние знаки относятся к случаю работы вариатора в мультипликаторном режиме, нижние - при работе вариатора в редукторном режиме.

Для МСХ планетарных импульсных вариаторов с большим числом роликов жесткость можно считать постоянной [611, и тогда потенциальная энергия МСХ вариатора запишется

2П = с Щ\ (фО - фа] + [Фа (Фх) - ФП-

где с - жесткость МСХ; Ф1(ф1) и ФаСФх) - углы поворота ведущих звеньев соответственно MCX-I, вступающего в работу, и разгружающегося МСХ-П. -

Обобщенные моменты, соответствующие выбранным обобщенным координатам, равны

Мф, = Met;, , .

где Мд и Me - соответственно движущий момент и момент сил сопротивления.

Тогда движение звеньев планетарного импульсного вариатора на участках заклиненного состояния МСХ будет описываться следующей системой нелинейных дифференциальных уравнений:

Aii Л2Ф2 + с [Фг (ф1) - ф2] Ф1 (фО -Г

+ с [Ф2 (фО - ф2] Фг (Ф1) = Мд Me;

: -f Бфз - с [Ф1 (Ф1) - Фг! - с [Фа (Ф1) - Фа] = MJ

Ai = / 4- /к + kA (птз 4- Шо) kJo +

А2 = kJoJeiz, Ф1(Ф1) = %?11; ФИфх)=

Заклинивание MCX-I будет начинаться, когда Ф2== ФюФхСФю),

где Фю - значение угла Ф1 в момент начала заклинивания; Фю - значение угловой скорости ф в момент начала заклинивания. При

ф2= Ф1Ф2 (- + Ф1)

МСХ-П будет полностью расклинен. Начиная с этого момента, в уравнениях (3) следует положить с = 0. Однако для решения, системы дифференциальных уравнений (3) нет начальных условий

Фю = Ф1 (0), Фю = Ф1 (0), Ф20 == Ф2 (0),

Ф20=Ф2(0),

при которых происходит вступление в работу MCX-I. Поэтому при решении системы уравнений (3) удобно воспользоваться мето-

ДОМ последовательных приближений. Первые начальные условия выберем из условий кинематики

Ф1(Ф10) = Ф2(+Ф10),

откуда находится значение ф- Затем вычисляется ФаСО):

Ф2 (0) = ©1Ф1 (Фю), (7)

где coi - угловая скорость ведущего звена вариатора, которую можно принять равной номинальной угловой скорости вала двигателя

Ф1о = 1- (8)

В момент начала заклинивания MCX-I ФаСФю) - Фа(0) = 0. (9)

Таким образом, из условий (6), (7), (8) и (9) находятся все первые начальные условия. При рассмотрении последовательно работы нескольких преобразующих механизмов начальные условия будут уточняться из условий периодичности функции Фа = = ФгСО ДО требуемой степени точности.

Зная законы движения звеньев вариатора, угол относительного поворота I обойм МСХ определим так:

ПО = Ф ГФ1(01-Ф2(0- (10)

Получить решения для системы нелинейных дифференциальных уравнений (3) в общем виде не представляется возможным. Решения данной системы легко получить с помощью ЭЦВМ. Однако для данной системы уравнений-можно получить приближенные решения [11, 65], позволяющие выявить влияние различныхпараметров системы на динамику заклинивания МСХ. Для получения приближенных решений воспользуемся методом Интегрирования по участкам. При этом разобьем период рабочего цикла преобра-зу1рщего механизма на участки, на которых передаточное отношение fa преобразующего механизма в силу незначительности его изменения в период рабочего цикла примем постоянным, а угол поворота Ф (Ф1) ведомого звена преобразующего механизма будем считать линейной функцией, учитывая малость рассматриваемого участка:

Ф (фО = Фо/ + ФЬ/ф,

где ф = ф1 - фод.

После линеаризации с- учетом выражений (11) система (3) примет вид

Л 1ф =Р л2ф1 + л4ф - Азу == Мд Me - с (?01фО/1 + ?02фо/2); (12)

=i= Лгф! + Вф2 - Лйф + Biy = Mciz + с [lui + 02),