Рассматривая треуголькики АВОх и А2В2.О1 и принимай значения Vn, и Vmai, получим

г\-\-г1-2г1Г2С08А5° (1)

rl-\-4+ COS 45° >(r3 + rf- (2)

Этими неравенствами ограничиваются длины звеньев преобразующего механизма при значении > 45°. Разделив неравенства (1) и (2) на и обозначив -= с, найдем

(7-У+(-т)-1414-<(-1) (3)

1,414 А (4)

Если принять некоторое значение с постоянным и рассмотреть выражения (3) и (4) как равенства, то получим два уравнения второй степени с текущими координатами и -у- :

(т-)+(-тУ-Ь414=(-1); (5)

(т-У + (-тУ + 414- - + if- (6)

Чтобы установить вид кривых, представленных уравнениями (5) и (6), составим определители А и Лзд из коэффициентов каждого из этих уравнений.

Для уравнения (5)

- 0,707 О

0,707 О 1 О

О -(c-iy

-0,5(с-1)2.

Так как с > 1, то Л =f О и линия второго порядка не представляет собой двух прямых

*0,5>0.

11 12 - 1 -0,707

21 22 -0,707 1

Для уравнения (6) аналогично определяем

Л-0,5(c-f 1)20; Лзз =г0,5>0.

Следовательно, уравнения (5) и (6) представляют собой уравнения эллипсов. Центру эллипсов находятся в начале координат. Уравнения осей симметрии (главных диаметров)

Оси симметрии эллипсов повернуты относительно осей координат и -у- на угол 45°.

Для удобства построения и исследования эллипсов, выраженных уравнениями (5) и (6), введем новую систему координат х я у, в которой оси координат совпадают с направлениями осей симметрии. Тогда уравнения эллипсов в канонической форме будут иметь вид

[1,85(с-1)]2

[0,765 (с-1)]

= I;

[0,765(с+1)]

[1,85 (с + 1)]2

, 0,7,(i+i);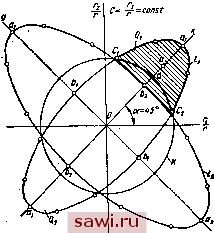

Рис, 2

По этим уравнениям при некотором постоянном значении с на рис. 2 показаны эллипсы l- и 1. Большая ось эллипса равна

001 - 1,85 {с - I). Малая полуось равна

Obi = 0,765 (с - I).

С уменьшением (с- 1) обе полуоси Оа и ОЬ эллипса li будут,уменьшаться. Это доказывает, что неравенство (-3) определяет собой область значений и -у-, лежащую внутри эллипса li-

В эллипсе I2 большая полуось направлена по оси у и равна

002 = 1,85 (с +1),

а малая полуось направлена по оси х и равна

ОЬг = 0,765 (с + I). .

Обе полуоси Ояг и Obz эллипса 1 будут увеличиваться с возрастанием (с + 1). Из неравенства (4) можно заключить, что

оно определяет собой область значений -у- и , лежащую вне

эллипса.

Это указывает на то, что неравенства (3) и (4) определяют в совокупности области Qi и Qj, заключенные между эллипсами 1

и /а в первом и третьем квадрантах. Так как величины и

~ существенно положительны, то неравенства (3) и (4) будут

определять область в первом квадранте. Эта область на рис. 2 заштрихована. При выбранном значении с только те механизмы удовлетворяют условиям > 45° и уах < 135° и, следовательно, могут быть использованы для преобразующего механизма

передачи, у которых значения -у- и являются координатами

точки, лежащей внутри или на границе заштрихованной области. Размер заштрихованной области в направлении оси х

= Oai - Oba = 1,85 (с - 1) - 0,765 (с + 1),

или, подставляя значение с - 162= 1,085 -2,615.

получим

(10)

При постоянном значении Гз с увеличением г величина аба уменьшается, т. е. с увеличением г уменьшается заштрихованная область, ограниченная эллипсами / j и / j. Максимального значения величина г достигает в том случае, когда аЬ = 0.

Тогда

W = 0,415гз.

При значении г = Гп,ах соответствующие эллипсы 1 я 1 будут касаться друг друга своими вершинами, а заштрихованная область, ограниченная ими, превратится в точку а, лежащую на оси X. Соотношение (11) определяет наибольший кривошип преобразующего механизма передачи при предельных значениях угла передачи.

Так как в процессе регулирования передачи величина эксцентриситета г изменяется от О до наибольшего значения, то, приняв во внимание формулу (11), можно определить возможные пределы изменения г:

О <г < 0,415гз.

(12)

В проворачивающемся кривошипно-коромысловом механизме кривошип г является наименьшим звеном.

Область Qi относительных размеров звеньев преобразующих механизмов включает в себя и симметричные механизмы, коэффициент изменения скорости хода которых равен единице.

На рис. 3 показан симметричный шарнирный четырехзвенный механизм ОЛ ВО 1, причем обозначения длин звеньев те же, что и на рис. 1. В таком механизме крайним положениям коромысел 266

OiBj и OiBa соответствуют положения кривошипа ОЛ1 и ОЛа, повернутые относительно друг друга на 180°.

Из вершины равнобедренного треугольника ВуОВ проведем медиану С. Очевидно, что CBj = СВ и ОС - г х-

Величина г определяется из треугольника ОхСВ.

Г = Г2С05у. (13)

Из треугольника OCOi следует

r = Ai + (OiC)l.

Так как ОС = rig у,

r, = yT7iV- (14)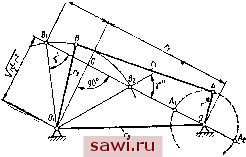

Рис. 3

Для симметричного механизма v =y - Если принять угол v равным минимально допустимому углу передачи

Y = ?д = 45°,

то по формуле (13) получим максимальное допустимое значение

длины кривошипа симметричного механизма = Га cos 45°. В этом случае

(15)

(16)

/l =-]/ !- 4ах.

Принимая угол передачи, соответствующий крайним положениям коромысла, равным д, получим механизмы, у которых минимальный угол передачи, будет несколько меньше уд. Такое положение можно считать допустимым для механизма передачи, так как у очень мало отличается от минимальных значений углов передачи, а углы передачи во время рабочего движения значительно превосходят у.

Подставляя в формулу (И) гл. 3 значение г из формулы (13),

получим

Решив это уравнение относительно угла у и приняв во внимание соотношение 7 > 45°, получим

(18)

arccos (-i) > 45°.

Последнее неравенство выражает те ограничения, которые накладываются на для симметричных механизмов. Симметрич-

ные механизмы только тогда могут быть использованы в качестве преобразующего механизма передачи, когда при заданном in выполняется неравенство (18),

Ранее было установлено (см. стр. 88), что минимальная величина iin = 0,78. Подставляя это значение и значение у = 45° в формулу (17), определим предельную минимальную величину передаточного отношения для симметричных механизмов:

пип ~ 1Д

Из прямоугольных треугольников ОуСВ (рис. 3) и ОСО следует

OCyii; г==г? + г-Л (19)

Разделив обе части уравнения (19) на г а приняв - = с, получим

(20)

Уравнение (20) представляет собой в системе координат -7 ) и (см. рис. 2) окружность k при ранее выбранном значении с. Часть этой окружности CiC, проходящей ч£рез заштрихованную область, удовлетворяет условиям 7п п > 45° и < 135°.

Таким образом, если в качестве основного механизма передачи выбран симметршчный кривошипно-коромысловый механизм, то

значения -y-j и (~- при выбранном значении с обязательно

должны изображать точку, лежащую на участке СС окружности k. -

Ранее было указано, что симметричные механизмы дают наибольшую равномерность движения ведомого вала. Поэтому для обеспечения равномерности его движения следует отдать предпочтение этим механизмам. Однако сама конструкция не вСегда позволяет осуществить симметричный механизм. Кроме того, в тех случаях, когда необходимо увеличить диапазон регулирования, приходится применять асимметричный механизм.

Заштрихованная область Qi, разделяемая на две части дугой окружности С1С2, дает представление о том, в какой части этой области следует выбирать точки, определяющие относительные размеры звеньев механизма. Если желательно иметь передачу с наибольшей равномерностью, то выбирают точку k на дуге окружности.

С целью повышения скорости ведомого вала следует выбрать точку в области, лежащей между дугой СС и эллипсом 1, так

как в этой области величина -у-j будет при одном и том же зна-

чении меньше, нежели в другой части а следовательно,

передаточное отношение механизма будет также меньше. Область, лежащая выше линии CiCg, менее важна, так как механизмы, соответствующие этой области, имеют большое значение -у-, а это значит, что диапазон регулирования частоты вращения этих механизмов получается меньшим. Необходимо также отметить, что механизмы, у которых значения (-j- и -у- при выбранном с, отмеченные точкой на границе заштрихованной области, имеют Vmin = 45°, а механизмы, относительные размеры звеньев которых -у- и при этом же значении с изображают точку внутри заштрихованной области Q, имеют yjm > 45°. Поэтому с целью увеличения Vmin необходимо стремиться выбирать значения (- и -у- так, чтобы они соответствовали точке, лежащей внутри области Q и наиболее удаленной от ее границ. Для симметричного механизма такой точкой является точка d пересечения дуги С1С2 и большой полуоси эллийса 1 (см. рис. 2).

Если в системе координат -у-j , -у- при допустимом минимальном угле передачи ущ = 45° для последовательных значений с = -у- построить области, Ограниченные эллипсами /1 и I2, изображающими уравнения (5) и (6), и провести соответствующие окружности по уравнению (20), то получим диаграмму (рис. 4), которая может служить для определения размеров звеньев преобразующего механизма. >

Определение размеров (длин) звеньев преобразующего механизма зубчато-рычажной передачи. По заданным пределам регулирования Пщц, и Пщах об/мин И частоте вращения вала приводного двигателя tii определяем минимальное передаточное отношение передачи

(21)

Вместе с тем io, выраженное по формуле (11) гл. 3, равно .(i)..-. , (22)

Подставляя в эту формулу значение to из формулы (21), получаем

(23)

\ г / о Лщах 2

Используя выражение (12), выбираем г. При этом.необходимо учесть, что излишне больш9е значение г ведет к усложнению регулирующего механизма, увеличению габаритных размеров