Приравнивая правые Части выражений (13) и (14), имеем

г COS сф -f а) R - r~-- cos яз

После преобразования получим sin а ± ~- sin 2ib sin а

+ 2/-) cos я?

sin(

а== [K-2sin2i, + P(P: 2г) :;:rsinil3].

Подставляя в выражение (15) Кг

имеем

tgil3 = ctga:

(Ki- 1) sin а

(15)

(16)

Угол соответствующий чаще всего употребляемым значениям iCi = 8 иа = 7°, определенный по формуле (16), равен для механизмов с внутренней звездочкой 81° 54 и для механизмов с наружной звездочкой 84°.

Для построения логарифмической спирали необходимо установить направление ее полярной оси. Угол 9о, определяющий положение полярной оси, можно определить, если в уравнение (12) подставить значение радиуса-вектора из выражения (13), соответствующего точке контакта Р, т. е. г sin а о , ,1,

-- рбо ctg ф

- cos(i3a)

Решая это уравнение относительно 9о, получим

e = 2,3tgIg[-3l]. (17)

Зная положение полярной оси и величину и используя формулу (12), можно построить логарифмическую спираль профиля рабочей поверхности звездочки.

С целью упрощения при изготовлении рабочей поверхности звездочки профиль этой поверхности очерчивают по спирали Архимеда, которая в полярных координатах запишется

Р = ав. (18)

На основании рис. 9, 5 и е составим систему уравнений г sina = ;fcpi cos (р,-(-а); (19)

(R ::р г) sin а = pi cos р,; (20)

(21)

Решая совместно уравнения (20) и (21), найдем

sin а =

Ka2 + pf{/? -г) Учитывая, что Pi > а. можно приближенно записать

sin а =

R - r-

(23)

Величина угла а, определенная по формуле (23), весьма мало отличается от значения этого угла, подсчитанного по более точной формуле (22). Например, указанное различие в углах а для МСХ электростартеров отечественного производства не превышает 0,2%.

Совместное решение уравнений (19) и (20) дает

п = cos а - tg U, sin а/

(24)

Подставляя в формулу (24) значения tg р, и sin а, cos а, определенные из выражений (21) и (22), получим

P? + bpt + tpi + d=0, (25)

где Ь = 2 2R (R 2г); с R {R 2г) У.

x {R{R- 2г) - 2аЧ; d = aR (R 2гу.

Решая уравнение (25) в тригонометрической форме и отбрасывая мнимые значения корней, получим

Pi- ]/2/icos (б0° где ft =

(26)

Зс -/

Ф = arccos ; q =

263 9fcg 27d 54

Во всех рассмотренных механизмах и особенно в механизмах со звездочками, имеющими плоские контатные поверхности, для получения необходимого угла заклинивания следует выполнять диаметр ролика с большой точностью. Изменение размеров ролика вследствие изнашиваемости ведет к изменению угла заклинивания. Кроме того, при групповом распределении роликов каждому из них будут соответствовать разные углы заклинивания.

Для механизмов, имеющих звездочки с плоскими рабочими поверхностями, ролики, выпускаемые подшипниковыми заводами, непригодны вследствие недостаточной точности.

Все это указывает на необходимость создания механизмов со звездочками такой геометрии, которая бы обеспечивала постоянство угла заклинивания а независимо от диаметра ролика. Найдем образующую кривую /-/ (см* рис. 9, ж и з) рабочей поверхности звездочки при условии а = const.

Чтобы определить уравнение такой кривой в полярных координатах с полюсом в точке О из треугольника ОАО, представим соотношение между радиусом-вектором р и величинами R, г иа в виде

р = VR 2г (1 + cosa) {R г)

(27)

Так как цилиндрическая поверхность отверстия обоймы может быть выполнена обычными технологическими методами с весьма высокой, точностью и так как эта поверхность в процессе работы механизма подвержена незначительному износу, то есть основание считать величину R постоянной.

Положим а = const, тогда радиус-вектор на основании выражения (27) будет представлять функцию от параметра г. Этот параметр, в свою очередь, может быть представлен некоторой функцией от полярного угла Э, т. е. г = г (6) и уравнение (27), следовательно будет иметь вид

p = ]/i?2-2f(0)(l + cosa)[R:T:f(9)] . (28)

Это выражение указывает на то, что можно выбрать бесчисленное количество функций г =У {Q) и тем самым получить бесчисленное количество образующих кривых для рабочей поверхности звездочки. При этом образующие кривые будут обеспечивать постоянное значение угла а при различных диаметрах ролика.

Простейшая зависимость изменения г от полярного угла Э имеет вид уравнения архимедовой спирали: г = об. Тогда уравнение (28), можно представить так:

р = - 2ае (1 -f cosa) (R аЩ . - (29)

Величина а может быть определена, если известны номинальный радиус ролика г , допуск на изготовление ролика 2бг и допустимый износ Аг в процессе эксплуатации механизма. При изготовлении ролика по системе отверстия наименьшая-.,величина радиуса ролика

min

(б. + Агн). Воспользовавшись зависимостью г

аЭ, запишем

0 = - и г -(б, + Аг,) = а(е -АЭ),

где Э - полярный угол, соответствующий номинальному размеру ролика; А0 - изменение полярного угла, соответствующее уменьшению ролика.

В результате совместного решения этих уравнений получим

бл + Аг (3Q)

Ориентировочно можно принять А 9 = 4-=-10°, причем следует , учесть, что А0 с увеличением числа роликов уменьшается. Построе-

ние кривой по уравнению (29) не вызывает затруднений, так как при 0 = 0 радиус-вектор р = R. .

Схема механизмов с групповым расположением роликов на контактных поверхностях ведущего и ведомого звеньев МСХ, встречающихся в импульсных вариантах, показана на рис. 10. МСХ с попарно расположенными роликами между рабочими поверхностями обойм (рис. 10, а) использован в варианте Харьковского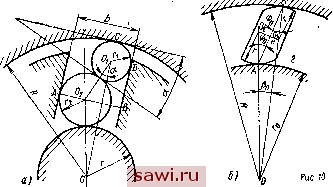

филиала НИИХИММАШа (см. рис. 34 в гл. 1). В соответствии с обозначениями на рис. 10, а угол заклинивания этого механизма определяется формулой

го (1/2го+г2) + -1(- -1 -Т2)-У1Ш

cosa =

(/i -f ч) {R - ri) R

Обозначим 1 = 4 77 p = 7Г ko ni2kr,A- Ы - fe, (1/21 - 1) - fep - 1 osa =--(fcp-f l)(fei-l)

откуда

feo = fep + 2 + 2[fei l)+ ,

(31)

+ (1- l)(p + l)cosa-f p + 1

(32)

Определив при расчете на прочнох ь или выносливость значения г и R и выбрав величину kp, найдем ko, а следовательно, и величину Го-

При Г1 = /-2 формулы (31) и (32) будут иметь вид

fe (1/20+1)4-1-2-l/2fef . 2(1-1)

cosa

ko \ + Y \ +2[k,{k,~ l) 2{k,~ I) cosa + 2

На рис. 10, б показана схема МСХ, в котором между цилиндрическими обоймами 1 VI 2 помещены тела заклинивания в виде эксцентричных роликов. Руководствуясь обозначениями, приведенными на этой схеме, из треугольника ОООо, найдем величин эксцентриситета е:

eV {R-rf + (ro + r)2-2(P-r)(ro + r)cosPo Очевидно, что угол

Ро == фо - iljo. но так как

Го sin Tj) R sin фо

Р ==фо-arcsin-iml.

, (33)

(34)

Так как обычно угол Ро < 1° 30, то можно принять cos Ро = 1. Тогда приближенная абсолютная величина эксцентриситета е = Го + 2г -

В механизмах с эксцентриковыми роликами, как было показано ранее, весьма важным параметром, определяющим нормальную работу механизма, является угол фо, который можно определить в зависимости от основных размеров механизма.

Из треугольника ОАВ следует

sin фо =. ;?sinPo -

Из уравнения (33) можно определить значение угла

cos 8 (R-rY + (ro + r)-e

(36)

Используя выражения (35) и (36), после преобразования можно получить

фо = arcsin R

(RJroY-e

4R-r) (Го + )

l 2(/? г)(Го + л)

(37)

У рассмотренного механизма радиусы г, которыми очерчены рабочие поверхности роликов, равны между собой. С целью повышения контактной прочности механизма увеличивают приведенный радиус кривизны в точке контакта ролика с внутренней обоймой за счет увеличения радиуса рабочей поверхности ролика со стороны этой обоймы.

Для этого механизма величина угла фо может быть определена по формуле (35). Угол Ро при этом найдется из выражения

cosPo

(J?-ri) + (ro + r2)-g

2(/?-ri)(ro-f Га)

(38)

где Ti, Га - радиусы рабочих поверхностей со стороны наружной и внутренней обойм.

РАСЧЕТ РОЛИКОВЫХ МСХ НА ПРОЧНОСТЬ

Общие положения. Основными критериями работоспособности роликового МСХ импульсных передач являются способность механизма заклиниваться без пробуксовки и контактная выносливость наиболее нагруженных элементов.

МСХ с цилиндрическими роликами выходят из строя вследствие усталостного выкрашивания и износа рабочей поверхности звездочки, а МСХ с эксцентриковыми роликами теряют работоспособность по причине поверхностного разрушения роликов. Циклическое движение, частое включение и выключение МСХ обусловливают изменения контактных напряжений в зонах контакта роликов с обоймами по пульсирующему циклу, что приводит к образованию трещин и к поверхностному выкрашиванию зон многократного нагружения (звездочки или эксцентриковых роликов). Кроме того, эти зоны подвержены износу вследствие перекатывания с проскальзыванием роликов в процессе заклинивания и расклинивания, а также скольжения роликов в период свободного хода.

Выкрашивание и износ можно ограничивать главным образом за счет соответствующей твердости материала роликов, звездочки и обоймы путем термообработки, применения вставок из твердых сплавов, снижения шероховатости контактных поверхностей повышения точности обработки роликов и сборки механизма.

Правильное заклинивание роликовых МСХ возможно при выполнении условия контакта ролика с обоймами в начальный момент заклинивания (см. стр. 164), а также условия самозаклинивания механизма в начальной стадии заклинивания и условия непробуксовки в процессе включения механизма при наличии деформации роликов и обойм.

Выполнение первого условия сводится к определению прижимного усилия с учетом динамики движения основных звеньев механизма, а второго условия - в основном к определению угла первоначального заклинивания а у механизмов с цилиндрическими роликами и первоначального угла давления фо у механизмов с эксцентриковыми роликами.

Если вопрос определения прижимного усилия с достаточной для практики точностью решается расчетом, то величины углов а и фо выбирают на оснований опытных данных конструирования и эксплуатации роликовых МСХ.