Для проектировочных расчетов на основании формулы (51) диаметр ролика

d = 0,432

ik W tg

(52)

где [т ] - допускаемое контактное напряжение сдвига.

Необходимо отметить, что в качестве роликов для МСХ, у которых рабочие поверхности выполнены в виде цилиндрических поверхностей, целесообразно применять ролики, выпускаемые под-шипниковой промышленностью.

Зная величину d, по выбранным значениям кя можно опре-делить величину R и /р.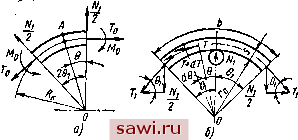

Рис 11

Ориентировочно у МСХ импульсных передач ki - 5-8, г = 5-=-20.

Для наиболее распространенных механизмов при = 8 и 2 = 2, а = 7°, £ = 2-10 кгс/cms [т] = 5000 кгс/см ([aj = = 15000 кгс/см) из уравнения (52) получим

d = 0,188/K. (53)

Рсшчет обоймы. В сечении наружной обоймы, если рассматривать ее как цилиндрическое кольцо, возникают напряжения от действия изгибающих моментов, нормальных и перерезывающих сил. У большинства конструкций обойм имеются концентраторы напряжений, которые должны быть учтены при расчете на прочность. Эластичные обоймы МСХ импульсных передач выходят из строя в результате усталостного разрушения. Поэтому такие обой-мы необходимо рассчитывать на выносливость.

Пренебрегая действием тангенциальных сил и предполагая, что давление на обойму со стороны роликов распределяется равномерно как между отдельными роликами, так и по их длине, расчетную схему наружной обоймы можно представить в виде кольца, нагруженного радиальными симметрично приложенными силами. В таком случае для определения напряженного состояния достаточно рассмотреть участок кольца, заключенный межйу этими си-31?

Лами (рис. И, а), быделенный элемент кольца будет находиться в равновесии под действием радиальных усилий Ai, изгибающих моментов Мо, нормальных То и перерезывающих усилий Qo-Из условий статики найдем

r = f ctge, = ctg.

(54)

В сеченииОЛ; ориентированном от правого конца элемента углом Э:

изгибающий момент

М = Мо + То?к(1 - cossinе

-Мо4

ctg -j-(l - cosO) - sine нормальная сила

т = То cos О + sm е = (ctg cos е + sine);

перерезывающая сила Q = То sin 9 - cos е =- (ctg sin е - cos в).

(55)

(56)

(57)

Зная, что угол поворота сечения правого конца элемента равен нулю, на основании теоремы Кастильяно и известной формулы по определению потенциальной энергии и кривого бруса запишем

EFh дМа

Т дМ

EF дМа

de = 0.

(58)

где Е - модуль нормальной упругости материала кольца; площадь поперечного сечения кольца; h - расстояние нейтральной оси криволинейного элемента до центра тяжести сечения.

Так как на основании уравнения (55) -щ- = 1, то после,подстановки значений М и Т из уравнений (55) и (56) в выражение (58) и интегрирования получим

(59)

AloA[(l+;)-ictg;.

Подставляя Мо из формулы (59) в уравнение (55), найдем выражение для изгибающего момента в любом сечении кольца:

Л1к [ i (1 + - 4- (tg Т- в + Sin 9) ] . (60)

Из анализа уравнения (60)*следует, что наибольший изгибающий момент будет при 9 = 0 (под силой), а наименьший при 9=91

(посредине между силами). Нормальные же усилия Т на оснований уравнения (56) будут наименьшими на концах элемента и максимальными в середине. Расстояние

Для прямоугольного сечения величина с будет найдена из быстросходящегося ряда: -

где S - толщина кольца; R - радиус кривизны окружности, проходящей через центр тяжести сечений.

При определении расстояния h для практических расчетов с достаточной точностью можно ограничиться первым членом ряда.

Тогда

j5i 12;?!

Величиной

н скобках Jлoжнo пренебречь, так как она

значительно меньше единицы, н тогда

Если в уравнение (60) подставим полученное значение Я, то максимальный изгибающий- момент (0 = 0) можно выразить

-12/?2

.ctg-

(61)

Полное нормальное напряжение в волокне кривого стержня, удаленном от нейтральной оси на величину определим по известной зависимости

где Мр - статический момент поперечного сечения относительно нейтральной оси; р - радиус кривизны волокна.

Для обойм прямоугольного сечения (наиболее частый случай) максимальное нормальное напряжение будет иметь место на внутренней стороне в сечении под силой. При этом

р=4; г/ = 4-/г; МрFh; FSl м R, = -±. 314

Максимальное нормальное напряжение на основании уравнений (61) и (62) будет

Wictg-

Мшах (S--2ft)

max - 2S/p ~ SlpDh

где D - диаметр отверстия обоймы.

(63)

Используя уравнения (61) и (63), определим толщину обоймы:

3WiCtg-i-D(fe+l)

2 {3 [а] /pD [ks + 1) - Л1 (а + &Ьк + 34) (Зз + 2) где [о! - допускаемое напряжение; -

(64)

ks=-; а = - -

3 .

. 2я 2 2

Для вычисления деформации б кольца в месте приложения усилия воспользуемся теоремой Кастильяно б =-р или после интегрирования и преобразований

fP г \ , NiR Г Зр , 2г (, , h\

\17 ~ 1г; + ~1F~ L 4<? kVrJ

yNiRp

4GFq

где G - модуль упругости сдвига материала кольца; Р

(65)

Для прямоугольного сечения кольца v = 1,5.

У большинства конструкций МСХ наружные обоймы значительно отличаются от цилиндрического кольца (их выполняют в виде головки шатуна или коромысла, венца зубчатого колеса, запрессованного в корпус кольца со шпоночными канавками, и . д.). Поэтому ниже приводится приближенный расчет.

Если принять, что ролики равномерно расположены по окружности, то часть кольца, ограниченную центральным углом -,

можно рассматривать как кривой брус (рис. И, б), закрепленный жестко на обоих концах.

Максимальная растягивающая сила

2 sin 01

2 sin

180°

(66)

Op =

максимальное растягивающее напряжение

2S/p Sin (i)

Учитывая, что высота S кривого бруса относительно мала, получим напряжения изгиба

и Г=-.

После подстановки i.5nyVi(/?+--)

Результирующее напряжение

2S/n

. / 180° \ s,n (-)

1,5я (2R + S) zS

откуда толщина стенки

4/р [а]

4,71

. / 180° \

4,71

2 4,7lRNi + Грг[а]

где [а]и - допускаемое напряжение на изгиб.

Для ориентировочных расчетов толщину обоймы находят в зависимости от диаметра d ролика.

Если наружную обойму запрессовывают в другую деталь, толщину стенки S определяют II431 по эмпирической зависимости

S = (0,5:-0,65) d,

а если обойму не монтируют в другую деталь, то

S = (0,8--1,2) d.

Для нормали мащиностроения МН-3-61 с учетом на ослабление шпоночной канавкой толщина обоймы

S = (l--l,6)d.

По мере увеличения размера механизма величина S по отношению к диаметру ролика уменьшается так, что в приведенной зависимости меньшие значения соответствуют большим размерам, а наибольшие - самым мальщ размерам механизмов. 316

Растягивающая сила Т (см. рис. 11,6) изменяется с изменением угла Э. Согласно выражению (66) средняя величина этой силы е,

1 01 J

.Л1 2 sin е

После интегрирования и подстановки 6 = - np = 0,3662lgtg(-f);

среднее напряжение растяжения 0,366ziVi Ig tg (у)

ср -

средняя радиальная деформация, соответствующая этому напряжению,

0,366/?yVi Ig tg (-)

Деформация изгиба от нагрузки Ni равна bNi l,93JVi (2/?-f

mEj

Суммарная деформация

ElryS

0,366 zR \g{g (-f)

1,93 (2R + .S)

(67)

Расчет механизма с наружной звездочкой. На основании формул (64) гл. 6 и (43), а также принимая во внимание, что приведенные радиусы кривизны в местах соприкосновения ролика со звездочкой и обоймой соответственно равны

найдем максимальные контактные касательные напряжения т и т в местах контакта ролика со звездочкой и обоймой:

,0,2./-

У zrJp(Ei + E

Ер) tg

, 02 f к 0 V zi,r

(£2 + £p)tg-2-

(68)

(69)

P = -4=l+-iL;

Рп Р