а амплитуда возмущающей функции угловых колебаний ?о V (2 sin р2 + 3 sin рз + ... + / sin +

-b(/l+/2 cos + +/ cos

Возведя в квадрат эти уравнения и приведя подобные члены, можно получить общие выражения амплитуд возмущающих функций для автомобиля с п числом осей:

zU = gl {п +2f(cos р2 + cos рз + . + cos? ) + cos (Ps - ) +

+ cos (P4-Рг) + + cos Фп-) + COS -Рз) + COS -h) +

+ ...+cos(p -P5) + ...+ cos(P -p i)i}; (21)

+ COS (fe - Рг)+... + /ая COS (p - p,) +... +

+ / -i cos.(P -p i)}. (22)

При подстановке в формулу (22) значений следует учитывать, что знаки и для осей, расположенных по разные стороны от центра масс, различны.

13. АНАЛИЗ ВОЗМУЩАЮЩИХ ФУНКЦИИ

Предварительное рассмотрение уравнений (21) и (22) возмущающих функций показывает, что существует сложная зависимость амплитуд возмущения как вертикальных, так и угловых колебаний от числа осей и их размещения по базе. Эти уравнения можно решать аналитическим и графическим методами. Функции возмущения в зависимости от длины неровности, рассмотренные применительно к гипотетическому четырехосному автомобилю с различным расположением осей по базе: равномерным (1-1-1-1), со сближенными промежуточными осями (1-2-1), тележечными (2-2) и неравномерным (1- 1-2), позволили установить закономерности связей размещения осей по базе, числа осей и длин неровностей с изменением возмущающих функций [2]. Максимальные и минимальные значения вертикальной возмущающей функции остаются постоянными для любого размещения осей по базе. Причем максимум

функции равен числу осей Zg тах/(Цо = П.

Максимум возмущающей функции угловых колебаний зависит от базы автомобиля, числа осей и размещения осей по базе. В общем виде для автомобиля с четным числом осей л и симметричным их расположением

Kmax/9ol = l0.5 -l-

где Б -ряд чисел: О, 2, 6, 12, 20, 30, 42 и т. д. 66

Анализ этого выражения применительно к четырехосному автомобилю показывает, что в пределах теоретически возможного изменения коэффициента i отношение фдтах/о изменяется на 50 %, в реально возможных пределах изменения коэффициента i изменение максимума возмущающей функции не превосходит 20 % Такое же соотношение имеет место и у шасси с другим числом осей.

Меньшее значение максимальных возмущений имеют автомобили с центральными сближенными осями. Однако пределы изменения возмущения при изменении размещения осей по базе небольшие.

Как и максимум возмущения вертикальных колебаний, максимум возмущения угловых колебаний находится в прямой зависимости от числа осей. Коэффициент пропорциональности возрастания максимума возмущения зависит от коэффициента размещения осей по базе i. Он равен л/2 при fmin=0, и минимальное значение имеет при imax-

Эти выводы являются правильными при принятых допущениях на первом этапе рассмотрения упрощенных выражений возмущающих функций, когда они не зависят от массы и момента инерции автомобиля. Если учесть более точное выражение возмущающей функции, представленное зависимостями (6) и (17), то вывод получается несколько иной. Так как с увеличением числа осей изменяются пропорционально масса и момент инерции подрессоренной части автомобиля и соответственно изменяется его база, то зависимость максимума возмущения вер> тикальных и угловых колебаний от числа осей имеет вид, представленный на рис. 18 [2]. -

С увеличением числа осей максимальное значение вертикальной возмущающей функции остается постоянным, а возмущающей функции угловых колебаний падает наиболее интенсивно при числе осей не менее шести, далее значения функции практически стабилизируются. Интересно отметить, что характер изменения возмущающих функций в зависимости от числа осей и их размещения по базе соответствует характеру изменения рассмотренных ранее частот и коэффициентов гашения колебаний.

Для получения графиков функций Zg/qo==f(Si S /L) и д/до=!{5и, Sail) при симметричных схемах шасси можно применять графический метод сложения косинусоид или более простой предложенный В. А. Борзенковым метод разделения многоосного ав-

Рис. 18. Изменение максимального значения возмущающих функций в зависимости от числа осей

томобиля HS яесколько двухосных ц грвфического сложения возмущвющих функций этих дэухосных автомобилей. При большом числе осэй и несимметричном их рдсположеиии по отноще нйю к центру Mflcc (ЦМ) приходится применять ЭВМ-

Построенные графическим методом и проверенные аналитически определением экстремальных точек возмущавдвдие функции предстаэлены на рие. 19. Следует отметить, что подобные графики били построены для автомобилей многих типов с различным числом осей (трех-, пяти- и шестиосных), Характер всех графиков одинаковый для всех автомобилей, и отмеченные ниже закономерности являются общими.

Анализ этих графиков показыввет, что протекание кривых ZqlqafiSnlL) или f{S) и щ1яа1{8) или !{$цЩ для любого расположения осей по базе в диапазоне длин гармонических не ровностей от 2 до 00 характеризуется следующими общими признаками; в диапазоне 2 м<йн<2 L, имеется несколько экстремальных точек как для угловых, так и для вертикальных воэ мущений;

при Sh<Z. максимуму вертикальной возмущающей функции, как правило, соответствует минимум угловой возмущающей функции и наоборот;

при Sn>L амплитуда угловых возмущений стремится к мак симуму, который наступает при S<Q;L, в затем при Sh--op асимптотически стремится к нулю;

при 8ц>\,Ы амплитуда вертикальных возмущений асимптотически стремится от минимуме к максимуму;

1-1-г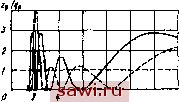

1-1-1-1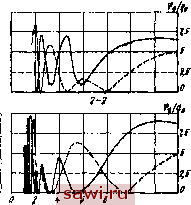

1-2-1

10 11 >ш

Рис. 19. Графики возмущающих функций вертикальных и угловых колебаний четырехосного азтомобнля с различным размещеинем осей по базе в зависимости от длины неровностей; ----.- -4>,/ .-f( ,)

При Sh< I м чередование максимумов и минимумов обеих возмущающих функций настолько частое, что определить характер возмущения такой неровности практически невозможно, к тому же на неровностях такой длины существенное значение имеют геометрические размеры шин и их сглаживающая способность,

Сравнение графиков, построенных для различных схем раЗ мещения осей по базе, указывает на их качественную общность;

для разных схем изменяется только длина неровности, вызывающая соответствующие возмущения, появление которых в реальных условиях эксплуатации равновероятно для любой схемы. Каждой схеме расположения осей по базе соответствуют конкретные, только ей присущие длины неровностей, вызывающие появление максимальных и минимальных возмущений;

чем дальше разнесены центральные оси, тем больше значение амплитуды угловых возмущений;

несимметричное размещение осей по базе приводит к тому, что во всем спектре дорожных неровностей не находится ни одной, которая не вызывала бы появления угловых колебаний;

в реальном диапазоне длин неровностей 2 .20 м добиться существенного уменьшения возмущения и, следовательно, вынужденных колебаний вследствие изменения схемы расстановки осей по базе практически невозможно. Следовательно, схеме размещения осей по базе не оказывает существенного воздействия на характер возмущения от дороги.

В гл. 1 было показано, что многоосные автомобили могут иметь различные степень подрессоривания колес и жесткость подвесок, Эти факторы влияют на возмущающие функции вынужденных колебаний, имеющих определяющее значение в формировании колебаний,

Из выражений возмущающих функций (17) можно установить, что многоосный многоопорный автомобиль с одинаковыми жесткостями подвесок всех осей (опор) будет иметь пропорционально меньшие значения возмущающих функций во всем диапазоне длин неровностей дороги. В случае, когда жесткости подвесок осей неодинаковы, выражения возмущающих функций выглядят иначе.

Для сравнения можно воспользоваться расчетом и построением возмущающих функций для четырехосного автомобиля, выполненного в двух вариантах; полностью подрессоренного и полуподрессоренного, у которого отсутствуют рессоры двух средних осей. Геометрические размеры автомобилей равны, расстановке осей по базе J-2-1, жесткости подвесок и шин одинаковы, амортизаторы отсутствуют. Полагая, что подрессоренные массы и моменты инерции подрессоренных частей обоих автомобилей одинаковы, можно принять их равными единице, жесткость шины больше жесткости рессоры в 3 раза; тогда она бу-

дет больше приведенной жесткости в 4 раза, т. е. Сш==ЗСр= = 4 С и Сш=6 кН/см. При этих условиях на основании уравнений (17) и (6) можно записать значение возмущающих функций:

для полностью подрессоренного автомобиля

Q,=2Сдо K4 + 4cosf!-f 4cosl,623p + + 2 cos 2,625? + 2 cos 0,625p sin N+Oi);

=2CqV20,97 + 9,45cosp-9,45cos 1,625p- 1,125 cosO,625p- 19,845 cos 2,625? sin Ы+а); для полуподрессоренного автомобиля

Q,=2Cq ]/34 + 32 cos 0,625? + 16 cos ? -j- +I6co&.l,625p + 2cos2,62Spsin (v + Ci);

=2Cq У 37,845 + 37,8 cos ? - 37,8 cos 1,625? - 19,845 cos 2,625?- 18 cos0,625 sin (v+Cj).

Расчеты no этим зависимостям показали, что максимум вертикальной возмущающей функции для полуподрессоренного автомобиля в 2,5 раза, а угловой возмущающей функции в 1,5 раза выше, чем у полностью подрессоренного автомобиля.

Из рис. 20 видно резкое отличие графиков возмущающих функций двух вариантов автомобиля не только по уровню амплитуд возмущений, но и по характеру кривых. Так, в интервале длин неровностей 1 ... 10 м для полностью подрессоренного автомобиля насчитывается пять точек, в которых вертикальные возмущения равны нулю, а для полуподрессоренного варианта в этом же интервале - лишь одна такая точка.

to\----

Sh,

Рис. 20. Графики возмущающих функций четырехосных автомобилей: ----полуподрессоренных;-- - полностью подрессоренных

Возмущающая функция угловых колебаний по характеру протекания примерно одинакова для обоих автомобилей. Максимумы функции расположены на неровностях одной длины, минимумы почти совпадают на неровностях до 2 м, промежуточные участки для каждого автомобиля имеют свой характер. Общий уровень возмущений выше у полуподрессоренного автомобиля, кроме возмущений на неровностях длиной 3,5... 5,5 м.

Рассмотренный пример подтверждает возможность разработки оптимальной схемы подрессоривания, если ставится задача получения высоких показателей плавности хода. Всякое упрощение подвески многоосного автомобиля ведет к ухудшению характеристик колебаний, компенсировать которое выбором схемы компоновки ходовой части невозможно.

14. ИССЛЕДОВАНИЯ ВЫНУЖДЕННЫХ КОЛЕБАНИИ МНОГООСНЫХ АВТОМОБИЛЕЙ НА ЭЛЕКТРОННЫХ И МЕХАНИЧЕСКИХ МОДЕЛЯХ

При исследованиях на АЭВМ вынужденных колебаний четырехосных и шестиосных автомобилей за базовую можно принять схему гипотетического автомобиля, полностью подрессоренного, с амортизаторами на всех колесах, сходного с испытываемой механической моделью. При решении дифференциальных уравнений (3) необходимо учитывать нелинейность изменения упругих сил. Система уравнений была приведена к машинному вид;у, составлены блок-схема набора задачи и методика ее решения [2].

Анализ графиков амплитудно-частотных характеристик колебаний подрессоренной массы автомобиля, полученных при решении задачи на АЭВМ, показал, что амплитуды вертикальных и угловых колебаний в условиях низкочастотного резонанса для одного и того же автомобиля резко отличаются в зависимости от длины неровностей.

Такое же различие имеет место и при условии изменения схемы компоновки ходовой части автомобиля (рис. 21). Таким образом, амплитуды колебаний меняются в зависимости как от схемы расположения осей по базе, так и от длины неровностей. В этих условиях отдать предпочтение той или иной схеме компоновки нельзя, поскольку все возможные варианты размещения осей по базе с точки зрения характеристик колебаний автомобиля равнозначны.

Результаты решения задачи для схемы 1-2-1, обработан- ные по максимальным перемещениям в области резонанса иа неровностях высотой 5... 10 см и длиной 2... 14 м, представлены в сравнении с соответствующими функциями возмущения на рис. 22. Как видно из сравнения, амплитуды резонансных колебаний, отнесенные к высоте неровности 100 мм, примерно пропорциональны соответствующим амплитудам возмущающих