цепного типа (см. гл. I). Каждая секция всех трех возможных расчетных схем имеет ходовую часть, подобную ходовой части одиночного обычного многоосного или многоопорного автомобиля.

При разработке расчетной схемы и ее математическом описании приняты все допущения и методические приемы, изложенные в подразд. 9, применительно к исследованию колебаний многоосного одиночного автомобиля.

За обобщенные координаты можно принять: z - вертикальные перемещения центра масс платформы; ф -угловое перемещение платформы; а - угловое перемещение секций в продольной плоскости. Вспомогательные координаты и g те же, что и для одиночного автомобиля (см. подразд. 9).

Примем обозначения:

Ml, Mi, Mo - массы секций, платформы и всей системы М=

/ь/2,/о - центральные моменты инерции секций и платформы.

Все обозначения показаны на рис. 25, индексы при обозначениях относятся к секциям (1 и 2) и платформе (0), обозначение без индекса - ко всей системе.

В динамической системе действует группа сил и моментов, аналогичных ранее рассмотренным в подразд. 9, Дополнительные силы и моменты обусловлены наличием в сцепке упруго-демпфируемой связи, работающей при складывании звеньев на угол а.

Динамическая система имеет -t-3 степеней свободы, следовательно, математически она может быть представлена системой п+Ъ связанных дифференциальных уравнений второго порядка. В общем виде эти уравнения могут быть записаны;

(23)

Первое уравнение представляет собой сумму проекций всех действующих сил с учетом сил инерции на ось Z. Оно описывает движение центра масс системы. Второе уравнение -сумма моментов относительно условной оси, определяемой обобщенной координатой ф. Это уравнение получается на основе использования теоремы о моменте количества движения по обобщенной координате ф.

Приведенные моменты инерции системы:

J9а = Jir2/(ri + Г2) - / l/C-l + Г2) = JiKn -J-iKfl.

Во втором уравнении системы (23) верхние знаки выражений в скобках правой части принимаются для сил, смещенных вперед относительно центров масс секций, а нижние -для сил, смещенных за центры масс (по ходу автомобиля).

Третье уравнение аналогично второму представляет сумму моментов количества движения по обобщенной координате а, в котором Ja = hK\\-\-J2K\i\ (Хцца -момент сопротивления ГЦВС; (д,ц - коэффициент сопротивления ГЦВС; Cha - момент упругой связи при складывании, имеющий линейную жесткость С.

Остальные п уравнений описывают колебания неподрессоренных масс. Они аналогичны уравнениям, рассмотренным в подразд. 9.

Представленная система дифференциальных уравнений в пределах принятых допущений позволяет с помощью ЭВМ решать любые задачи по колебаниям сочлененных автомобилей любой известной в настоящее время конструктивной схемы. Для решения задач применительно к сочлененным автомобилям прицепного типа, когда общая платформа отсутствует, в уравнениях необходимо массу и момент инерции платформы приравнять нулю Мо=0,/о=0.

При отсутствии сцепного устройства, ГЦВС и упругой связи величины, описывающие их в уравнениях, следует приравнять нулю.

Среди всего многообразия сочлененных автомобилей большое распространение имеют автомобили, характеризуемые симметричной схемой компоновки, у которых /(w/j; riMi ; 2М2 и ri = Li, Г2=/-2. Симметричность сочлененного автомобиля позволяет значительно упростить дифференциальные уравнения колебаний:

Здесь

/=Ср ii-z- Si - й,а) -1- 2 {(- z - Si - bfl) ; Ж = + Ж2 + Ло; =-1 + -2+0+-ii + r\Mi,

Расстояния Ь,- и 5,- с соответствующими знаками приведены ниже применительно к восьмиосному симметричному автомобилю (по четыре оси в секции), п = 8 (обозначения показаны на рис. 25):

I... 1 2 3 4 5 6 7 8

bi...ln ki -k\ ~-U\ -hi -кг hi hi

Si...ri + U Ti+Zji Г1-/31 /-1-/41 -Ti+hi -ri+hi -Ti-ki -ri-hi

Для симметричной схемы автомобиля выполняются условия: 2й, -0; 25,=0 и 2&,-5,=0, поэтому исходные уравнения можно полностью разделить так, что амплитуды обобщенных координат г, ф и а можно определять из хорошо известных уравнений, описывающих простейшие эквивалентные двухмассовые системы, изображенные на рис. 26. Для определения z следует ввести для п-осного автомобиля вспомогательные переменные:

Тогда Z определяется из следующей системы уравнений:

M,z=F,;

mi=R,-F,\

/=-,==Cp(C-2) + 2tiC-2);

Для определения угловых колебаний симметричной системы по двухмассовой расчетной схеме вводятся вспомогательные переменные, физически характеризующие линейные перемещения условной точки платформы, расположенной на расстоянии 0 от центра масс системы. Эквивалентная схема при этом такая же, что и при определении z (рис. 26, а), и отличается только обозначениями (на схеме обозначения даны в скобках):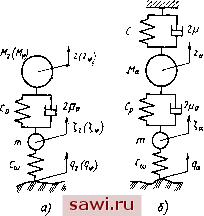

Рис. 26. Приведенные расчетные схемы симметричных сочлененных

автомобилей: а - вертикальных колебаннй; б -угловых колебаний

1 1 1

Тогда система дифференциальных уравнений примет вид:

M,z,f=F,;

F Ср (С;р - z) -f 2 (Су - z,); ni=Rtf - F\

где Mf=Jh.

Аналогично и при определении угла складывания секций в вертикальной плоскости нужны новые переменные для условной

точки, лежащей на расстоянии =/2

Применительно к примут вид:

расчетной схеме (рис. 26, б) уравнения

где AIJje\

В данной расчетной схеме в отличие от предыдущей появляются дополнительный амортизатор с эквивалентными коэффициентами сопротивления цэ = ЛцЛц2/9 и дополнительная рессора с эквивалентной жесткостью Сз=СксЩ.

Пользуясь эквивалентными схемами, аналитическим путем можно определить основные характеристики колебаний сочлененного автомобиля по обобщенным координатам z. (р и а. Эти уравнения удобны для проведения прикидочных предварительных расчетов при проектировании сочлененного автомобиля. Определить координаты или их производные можно при синусоидальном возмущении, а по построенным частотным характеристикам- и при случайных возмущениях. Частотные характеристики при этом зависят не только от параметров колебательных схем, но и от эквивалентных возмущающих функций Zq, щ и а которые при гармоническом профиле пути могут быть точно определены аналитически. Если (х) - ордината профиля пути, отнесенная к центру масс всей системы, то возмущение под i-м колесом

д = (7(г / + 5,),

где t-время; v - скорость движения.

Б частном случае для синусоидального профиля пути, как было указано выше в подразд. 12, q(,x) =*0,5Яв51п 2nxJSe (где На - 82

высота неровности), тогда

gi(i)H sin 2rt(t)/ + Sj)/S ,

где Si - координата i-го колеса (оси) относительно ЦМ.

Из этого выражения можно найти эквивалентные возмущения для симметричной расчетной схемы

2,(/) =

2я (,vt + Si)

и амплитуду возмущения (см. подразд. 12, 13)

2nSi

2я5,

Аналогично определяются эквивалентные возмущения: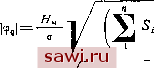

2jtS,

2я5;

bi sin

2nSi

На основе расчетов по приведенным выше зависимостям и экспериментальных исследований на моделях сочлененных автомобилей, выполненных рядом исследователей, можно отметить ряд интересных закономерностей колебаний этих автомобилей.

Прежде всего можно установить, что определяющее влияние на формирование характеристик колебаний сложной системы оказывают характеристики колебаний отдельных звеньев (секций) и характеристики упругой и демпфирующих связей между звеньями сочлененного автомобиля.

Закономерности изменения характеристик колебаний отдельных звеньев те же, что и для одиночных жесткорамных автомобилей.

Для получения высоких показателей плавности хода как многоосного одиночного, так и сочлененного автомобиля основное внимание должно быть сосредоточено на выборе оптимальных характеристик подрессоривация колес секций (жесткости, величины статических и динамических ходов подвески, величин гашений и сухого трения в подвеске и др.). Существенного влияния на колебания сочлененного автомобиля изменение числа осей и расстановки их по базе секций так же, как в случае одиночного автомобиля, оказать не может.