Глава III

ВЕРТИКАЛЬНЫЕ ДИНАМИЧЕСКИЕ НАГРУЗКИ В ХОДОВОЙ ЧАСТИ

Наиболее нагруженными элементами автомобиля являются узлы ходовой части; степень нагруженности последней определяет надежность всего автомобиля при его эксплуатации. Поэтому важно рассмотреть влияние общих конструктивных решений на нагруженность ходовой части и установить их связь с эксплуатационными свойствами.

Опытом испытаний автомобилей любого типа установлено, что доработка элементов ходовой части является длительным и трудоемким этапом, а ходовая часть - наиболее уязвимой системой автомобиля. Кроме того, общие конструктивные решения в значительной степени определяют работоспособность ходовой части и надежность деталей трансмиссии.

18. ОБЩИЕ И ИСХОДНЫЕ ПОЛОЖЕНИЯ

Исследованию динамических нагрузок, вызываемых взаимодействием колеса автомобиля с неровностью дороги, посвящено много работ. Однако их анализ позволяет установить, что вопросы влияния динамических нагрузок на характеристики ходовой части многоосных и многоопорных автомобилей в реальных дорожных условиях и влияния схем ходовых частей на эти нагрузки исследованы еще недостаточно. Установлено, что прочность узлов и механизмов ходовой части автомобиля зависит в основном от динамических вертикальных нагрузок, возникающих при движении по неровным дорогам и вне дорог. Горизонтальные силы, действующие на ходовую часть, хотя и не ограничиваются условиями Сцепления колес автомобиля с дорогой, по абсолютной величине являются несоизмеримыми с вертикальными нагрузками. Если не учитывать аварийного случая удара колеса в вертикальную стенку, то по экспериментальным данным в нормальных условиях эксплуатации горизонтальные силы составляют 10...12% вертикальных сил. Этот вывод позволяет из всего комплекса нагрузок, действующих на ходовую часть, исследовать вертикальные динамические нагрузки, как определяющие в основном прочность ее узлов и деталей, и также режим работы трансмиссии автомобиля и такие его эксплуатационные свойства, как проходимость, управляемость, устойчивость и др.

Особую актуальность приобретает исследование вертикальных нагрузок в связи с появлением многоопорных автомобилей, перевозящих грузы массой до несколько тысяч тонн (см. разд. 6).

Динамические нагрузки на ходовую часть автомобиля определяются совокупностью сил тяжести и инерции, а также перераспределением силы тяжести между осями. Из всего многообразия условий движения можно выделить наиболее характерные случаи нагружения ходовой части: максимальные динамические нагрузки, вызываемые колебаниями подрессоренных и неподрессоренных масс; перераспределение нагрузок между осями многоопорной системы при переезде через различные дорожные неровности и препятствия; перераспределения, вызываемые действием на автомобиль горизонтальных сил.

Поэтому вертикальная нагрузка, действующая на ось, опору (кронштейн, рычаги и др.) в общем случае может быть условно представлена в виде

Р,=Р,ЛРп + РЛР., (24)

где Рд -наибольшая нагрузка на ось при движении; ст - статическая нагрузка, определяемая силой тяжести подрессоренной массы; Рц и Рг-нагрузки, обусловленные перераспределением силы тяжести между осями соответственно при наезде на неровность с малой скоростью и под действием горизонтальных сил на корпус автомобиля (силы инерции при разгоне и торможении, сопротивления воздуха, тяги на крюке или седельном устройстве и т. п.): Рк-нагрузка, определяемая колебаниями подрессоренной и неподрессоренной масс.

Для оценки динамичности вертикальных нагрузок принят коэффициент динамичности, показывающий, во сколько раз динамическая (с учетом статической) нагрузка Рд превосходит статическую:

K,==PJP . Разделив обе части уравнения (24) на

Рст> можно получить

выражение для коэффициента динамичности вертикальных нагрузок:

К,= 1+К + К,+К (25)

где /Сп - коэффициент перераспределения нагрузки на ось (опору) при наезде на неровность; /Ск - коэффициент динамичности нагрузок от колебаний подрессоренных и неподрессоренных масс; Кг - коэффициент перераспределения нагрузок на ось под действием горизонтальных сил.

Влияние каждой составляющей уравнения (25) зависит как от конструктивных особенностей и схемы автомобиля, так и от скорости движения и состояния дорожного полотна. Например, при движении автомобиля по дорогам с неровностями большой длины основное влияние на вертикальные нагрузки окажут колебания подрессоренной массы, при движении по коротким неровностям - колебания неподрессоренных масс, а при переездах че-

рез неровности дороги или каналы, кюветы, насыпи - перераспределение нагрузок между осями. Очевидно, что анализ динамичности нагрузок и влияния общих конструктивных решений целесообразно провести по каждой составляющей уравнения (25) в соответствующих дорожных условиях.

19. ВЕРТИКАЛЬНЫЕ ДИНАМИЧЕСКИЕ НАГРУЗКИ, ОПРЕДЕЛЯЕМЫЕ КОЛЕБАНИЯМИ ПОДРЕССОРЕННОЙ И НЕПОДРЕССОРЕННОЙ

МАСС

Нагрузки на ходовую часть наиболее интенсивны при колебаниях шасси, возникающих при резонансных или близких к ним скоростях, когда амплитуды колебаний достигают максимальных значений.

При изучении динамических нагрузок, обусловленных колебаниями двухосных автомобилей, различают воздействия двух типов, вызванные переездом длинных и коротких неровностей. Такой подход может быть применен и к изучению динамических нагрузок многоосных автомобилей. Правомерность данного упрощения при достаточной разнице между низкими и высокими собственными частотами и при одном порядке времени действия возмущения и периодов низкочастотных колебаний убедительно показана в работах проф. Р. В. Ротенберга. Допустимость этого метода подтверждают также одинаковые соотношения низких и высоких частот у двухосных и многоосных автомобилей. Проведенные эксперименты на моделях показали, что при переезде четырех- и шестноснымн автомобилями неровностей со скоростью, близкой к низкочастотному резонансу, большие перемещения имеет подрессоренная масса, а колеса копируют профиль неровности, т. е. неподрессоренные массы не оказывают существенного влияния на колебания груза и на нагрузки в ходовой части.

При движении со скоростями, близкими к скоростям, соответствующим высокочастотному резонансу, подрессоренная масса остается практически неподвижной, а колеса совершают колебания, поэтому колебания груза почти не влияют на нагрузки в ходовой части, а решающее влияние оказывают колебания неподрессоренных масс.

Под длинными и короткими неровностями следует понимать такие неровности, продолжительность воздействия возмущающих функций от воздействия которых близка соответственно к периоду собственных колебаний подрессоренной массы и к периоду колебаний неподрессоренных масс автомобиля.

При исследовании нагрузок на ходовую часть от колебаний подрессоренной и неподрессоренных масс целесообразно рассматривать эквивалентные схемы динамических систем для случаев движения по коротким (рис. 31, а) и длинным неровностям (рнс.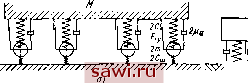

УХЧЧУ,

Рис. 31. Расчетные схемы нагружения ходовой части многоосного автомобиля

31, б). При колебаниях в области низких собственных частот, которые вызывают значительные вертикальные и угловые перемещения подрессоренной массы и соответственно большие перегрузки в ходовой части (при достаточной разнице низких и высоких собственных частот), можно пренебречь влиянием неподрессоренных масс.

Рассмотрение исследуемой динамической системы (рис. 31, а) позволяет установить, что при движении автомобиля по коротким неровностям в режиме высокочастотного резонанса ни число осей, ни размещение их по базе не оказывают существенного влияния на нагрузки в ходовой части. В данном случае нагрузки всецело зависят от конструкции подвески, параметров подрессоривания, жесткости шины, характеристик неровностей пути. В процессе исследований и испытаний многоосных автомобилей установлено косвенное влияние числа осей на нагрузки, вызываемые колебаниями неподрессоренных масс: чем больше число осей, тем больше вероятность длительного движения автомобиля при резонансном режиме колебаний колес. Это объясняется тем, что на многоосном автомобиле водитель, как правило, не Ощущает высокую (резонансную) нагружеиность колес и не принимает мер (изменение скорости движения) для выхода из резонансного режима. На двух- и трехосных автомобилях этого не наблюдается.

Таким образом, главное влияние числа осей и их размещения по базе на динамические нагрузки проявляется через колебания подрессоренной массы. Следует иметь в виду, что динамические нагрузки от колебаний неподрессоренных масс могут в 1,5...2 раза превосходить нагрузки, возникающие при низкочастотных резонансных колебаниях подрессоренной массы. Это необходимо учитывать при расчетах и исследовании общей нагруженности ходовой части любого автомобиля.

В общем виде силы, действующие в подвеске, показаны на рис. 15 и могут быть математически описаны выражениями (1) и (2). С учетом принятых в данной главе допущений обобщенная динамическая нагрузка от колебаний подрессоренной массы к=Спр2А. Здесь приведенная жесткость подвески имеет два значения: одно - в пределах динамического хода подвески без учета жесткости грунта Спр = СрСш/(Ср+Сш); второе -за преде-

лами хода подвески, когда приведенную жесткость определяют жесткости шины Сш, грунта Сгр и буфера сжатия подвески Су, а рессора выключается ограничителем хода подвески:

С р == СщСуСрр/(СуСш -р CyCj.p -j- СрСщ).

При отсутствии ограничителя хода подвески и параллельной работе рессоры и упора

Второе значение приведенной жесткости определяет максимальную динамическую нагрузку на колесо при пробое подвески.

Очевидно, что выбранная схема ходовой части на приведенную жесткость подвески не влияет.

Суммарная дополнительная деформация рессоры и шины 2А слагается из деформаций, вызванных угловыми колебаниями Дф = /ф, перемещениями шины при движении колеса по неровности Ak = 9i и вертикальными колебаниями Az = z. В случае независимого решения уравнений угловых и вертикальных колебаний суммирование указанных составляющих следует проводить с учетом фазовых сдвигов угловых колебаний по отношению к вертикальным колебаниям и к профилю пути.

Влияние этого фактора можно проиллюстрировать результатами экспериментального исследования колебаний механической модели, которые подтверждают известные теоретические положения образования фазовых сдвигов. На рис. 32 приведены осциллограммы записи профиля пути и колебаний подрессоренной массы (г и ф) в дорезонансном, резонансном и зарезонансном режимах движения модели четырехосного автомобиля без амортизаторов (коэффициент апериодичности 4 = 0,06.,.0,07). Экспериментальные исследования показали, что в резонансном режиме продольно-угловых колебаний максимальные амплитуды колебаний совпадают с экстремальными точками профиля пути. С точки зрения нагрузок на крайние колеса четырехосного автомобиля самым неблагоприятным моментом является наклон корпуса во впадине профиля, а с точки зрения отрыва колес движение на вершине профиля.

Таким образом, при движении автомобиля по волнообразному низкочастотному профилю наиболее нагружены передняя и задняя оси. При движении автомобиля в дорезонансном режиме наибольшие углы наклона корпуса приходятся на точки перегиба профиля дороги (фазовый сдвиг л/4). При движении в зарезонансном режиме наибольшие углы наклона приходятся на точки перегиба за вершиной профиля, что способствует большему отрыву передних колес от дорожного полотна. Однако происходит резкое гашение угловых колебаний и отрыва колес и их больших перегрузок не наступает.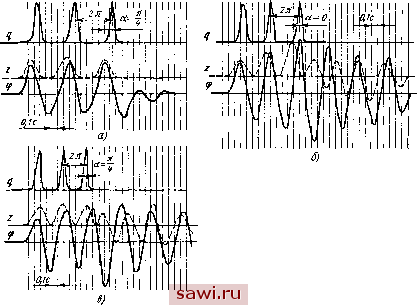

Рис. 32. Осциллограммы записи профиля пути и колебаний подрессоренной массы в режимах движения:

а -дорезонансном; б -резонансном; в - послерезонансном

По экспериментальным данным сдвиг по фазе между продольно-угловыми и вертикальными колебаниями зависит от соотношения их частот и коэффициентов апериодичности. При равенстве этих частот и коэффициентов максимальные амплитуды резонансных продольно-угловых и вертикальных колебаний не совпадают по фазе и имеют фазовый сдвиг л/2, т. е. г=0 при фтах, а ф = 0 при 2max дсформации подвески от колебаний не суммируются. При увеличении отношения шг/щ (иг>©ф) при резонансных продольно-угловых колебаниях максимумы амплитуд угловых и вертикальных колебаний будут по фазе приближаться друг к другу, а в пределе совпадут.

На рис. 33 приведены осциллограммы экспериментальных записей продольно-угловых колебаний ф и вертикальных колебаний Z при сог>Шф. Этот случзй являстся характерным для компоновки реальных автомобилей, максимальные амплитуды продольно-угловых и вертикальных колебаний совпадают по фазе, т. е. деформации подвески арифметически суммируются как при резонансном, так и при зарезонансном режиме продольно-угловых колебаний.

Таким образом, для резонансного режима движения реальных многоосных автомобилей, у которых сог>сОф, при расчетах суммарную деформацию можно определять без большой погрешности, не учитывая фазовых сдвигов 1,А=г+и(р + д1, тогда

(26) 101