По направлению потоков в узловых точках легко определить режим работы колеса. Так, у тормозящего колеса направление потоков противоположное по сравнению с показанным на рис. 43, б (кроме потока t). На ведомое колесо воздействует один активный поступательный - от рамы к колесу Мк, сок, реактивный Рк, Vk и рассеянный t потоки. Также можно представить свободное и нейтральное колеса.

При качении колеса в общем случае, когда на колесо дополнительно действуют боковая сила и поворачивающие моменты, обобщенная узловая точка колеса превращается в векторную узловую точку, и показанные на рис. 43 силовые потоки превращаются в векторные потоки, которые математически изображаются векторными величинами. Важно при этом отметить, что число силовых потоков и геометрическое изображение обобщенной узловой точки колеса не меняются. В дальнейшем будем пользоваться этим изображением.

На рис. 44 и 45 показаны схемы силового потока трансмиссии четырехосных автомобилей. На схемах ровной линией обозначены вращательные потоки, а линией с зубцами - поступательные потоки; Kin, Ки, Kin, АГ4Л - обобщенные узловые точки колес правых и левых колес автомобиля; б - разветвляющая точка, которая описывает отвод мощности для преодоления внешних сопротивлений, приложенных к автомобилю: сопротивление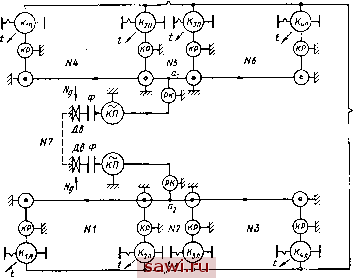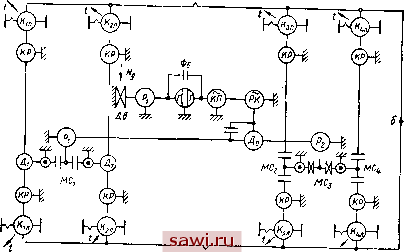

Рис 44. Схема силового потока бездифференциальной трансмиссии четырехосного автомобиля с двумя двигателями с бортовой раздачей мощности по

колесам

Рис. 45. Схема силового потока дифференциальной трансмиссии четырехосного автомобиля с одним двигателем и мостовой раздачей мощности по колесам

воздуха, сопротивление подъема и т. п. Остальные узловые точки описывают различные элементы; Дв - двигатель; Лд - мощность, эквивалентная энергии, потребляемой двигателем; КП - коробка передач; РК-раздаточная коробка; КР - колесный редуктор; Р -редуктор; Ф -фрикцион; Д -дифференциал; ГТ - гидротрансформатор; М - муфта свободного хода. Направление некоторых силовых потоков не показано, они могут иметь в каждом частном случае движения различное направление.

Анализ всех возможных схем силового потока трансмиссий существующих многоосных автомобилей позволил выявить общие свойства этих схем. Так, установлено, что с учетом возможности возникновения относительных потоков мощности через грунт силовые потоки многоосных автомобилей являются замкнутыми. Число отдельных замкнутых неравнозначных контуров равно 2п-1. Такими замкнутыми контурами являются контуры между колесами одной оси (левым и правым) и между осями; в схеме силового потока на рис. 44 - контуры между колесами каждой стороны автомобиля и межбортовой контур, замыкающийся через двигатели, обозначены номерами.

В зависимости от наличия и типа специальных узловых точек в этих контурах возможны при определенных условиях движения разветвляемые, циркулирующие или холостые потоки. В дальнейшем эти точки условимся называть развязывающими узловыми точками (РУТ). Такое название дано потому, что предназначение этих точек разомкнуть, развязать при необходимости замкнутый силовой контур. На рис. 44 в замкнутых силовых

контурах такие РУТ отсутствуют (во всех контурах), а на рис. 45 такие РУТ имеются во всех семи (№ 1... 7) контурах. В контурах первой, второй оси и в межтележечном контуре в качестве РУТ применены дифференциальные механизмы Du D2 и Do, а в тележках и в контурах задних осей - муфты свободного хода МСх, МС2, МСз и МС4, которые иногда ошибочно называют самоблокирующимися дифференциалами.

Задачей дальнейших исследований силового потока является определение минимально необходимого числа РУТ и целесообразного типа их механизма. С учетом решаемой общей проблемы исследование будет проводиться во взаимосвязи с общей схемой автомобиля.

Максимально возможное число РУТ равно числу замкнутых контуров в силовом потоке, т. е. 2 -1. Если принять такое число развязывающих механизмов и различных устройств, их заменяющих, то трансмиссия получится очень сложной и дорогостоящей в производстве и эксплуатации. Поэтому необходимо определить минимальное допустимое число РУТ, при котором не ухудшаются эксплуатационные характеристики автомобиля. Правильный выбор типа РУТ важен с точки зрения обеспечения хороших показателей проходимости, устойчивости, надежности, экономичности и других характеристик автомобиля.

В соответствии с общей теорией силового потока в начале его исследования должны быть определены задающие параметры системы. Общее число задающих параметров равно сумме задающих скоростных и силовых параметров

Х=Хи + Х, (41)

и соответствует числу свободных силовых потоков.

Число задающих скоростных параметров равно числу степеней свободы силового потока и определяется по формуле

>н=2(0. + 0к) + 0р-А-?,

где От, Ок и Ор -число обобщенных, кинетических и разветвляющих узловых точек; k - число связывающих потоков; ф - число уравнений кинематики, которое определяется схемой сило-вого потока.

Тогда из формулы (41) получим число силовых задающих параметров

Анализ задающих параметров применительно к схеме силового потока многоосного автомобиля в общем случае движения, когда поступательные потоки колес можно принимать свободными, показал, что для любой схемы тоансмиссии автомобиля общее число задающих параметров Х=2п+ 1, т. е. числу свобод-

ных потоков на колесах 2п и свободному потоку от двигателя. Число скоростных задающих параметров при отсутствии РУТ (блокированный привод) или известных их кинематических характеристик (в случае применения РУТ) будет Яи=1. Этим задающим параметром может быть скорость движения автомобиля или частота вращения коленчатого вала двигателя. Тогда Яд=2п+1-1 = 2п, т. е. число силовых задающих параметров равно числу ведущих колес. При расчете определенно можно задать только один параметр: или внешние сопротивления, или силовой фактор двигателя; 2п-1 параметров остаются неизвестными-задача является статически неопределимой 2 -1 раз.

Чтобы решить задачу по распределению мощностей в общем виде, вероятно, надо иметь дополнительные условия к общим уравнениям теории силового потока. Такими условиями в случае блокированной связи могут быть уравнения геометрических связей и уравнения упругих связей замкнутых контуров силового потока, которые можно получить 2 -1 (по числу контуров в схеме), т. е. столько, сколько необходимо для решения задачи.

В случае применения РУТ в контурах дополнительными уравнениями являются уравнения, описывающие закон распределения мощности в контуре, определяемый типом механизма РУТ. Например, если в качестве РУТ применяется симметричный дифференциальный механизм, то в контуре момент распределяется симметрично, поровну; если дифференциальный механизм несимметричный, то момент распределяется в соответствии с внутренним передаточным числом механизма; если применяется простая отключающая муфта, то в контуре будут холостые потоки, т. е. в одной из частей контура момент будет равен нулю.

Пока в самом общем виде уравнение упругости замкнутого контура без РУТ можно представить при малой скорости перемещений в такой форме:

A12=(?l--92)/Ynp,

(42)

где AMi2 -упругий момент в контуре 12; у р=у+уг+у ~, приведенная податливость контура, включающая характеристики тангенциальной эластичности шин, податливости грунта в контакте колес и податливости механических элементов контура; ф1-ф2 - уравнение геометрических связей, представляющее собой разность углов закрутки конечных элементов (колес или мостов) контура (кинематическое несоответствие элементов контура).

Таким образом, упругий момент, который, как будет показано, значительно влияет на распределение мощностей по колесам, зависит от приведенной податливости контура и кинематического несоответствия в контуре.

25. КИНЕМАТИЧЕСКИЙ АНАЛИЗ РАБОТЫ ТРАНСМИССИИ

Геометрические связи в замкнутом контуре силового потока влияют на упругий момент. Все исследователи трансмиссий полноприводных автомобилей учитывали в той или иной мере геометрические связи, выражая их разностью радиусов качения, разностью углов поворота колес или радиусов криволинейного движения. При этом рассматриваются отдельные составляющие кинематического несоответствия и расчет ведется только для частного случая. В действительности все многообразные факторы, влияющие на кинематическое несоответствие, воздействуют на работу трансмиссии одновременно, и суммарное значение кинематического несоответствия в конкретный момент определяет распределение мощностей по колесам.

Для учета этого и обеспечения возможности суммирования отдельных составляющих в качестве измерителя кинематического несоответствия можно использовать относительную величину - отношение разности путей, пройденных fe-м и т-м колесами (осями) за данный отрезок времени, к пути, пройденному первым (начальным) колесом (осью) замкнутого контура: .

lmk=[(Sm~S,)jSJ ЮОо/о = ±(1 -SJSJ ЮОо/о. (43)

Для упрощения анализа кинематического несоответствия причины его возникновения можно подразделить на три группы:

1) конструктивно-эксплуатационного происхождения, обусловленные состоянием и конструкцией самого автомобиля (различие радиусов качения колес, неравенство передаточных чисел приводов и т. п.);

2) вызванные криволинейным движением автомобиля в горизонтальной плоскости;

3) обусловленные профилем пути, макронеровностями дороги, препятствиями.

По типу замкнутого контура можно выделить межколесное и межосевое кинематическое несоответствие.

Конструктивно-эксплуатационные факторы. На основе общей зависимости (43) были получены частные формулы и проведен анализ факторов, влияющих на величину кинематического несоответствия в каждом конкретном случае движения автомобиля. Величина кинематического несоответствия конструктивно-эксплуатационного происхождения может быть определена по формуле

(44)

где г*в. Гтъ - радиусы качения -го и т-го колес в ведомом режиме, определяемые экспериментально (Mft=0); и*, Um - передаточные числа приводов колес.

Проведенные эксперименты показывают, что радиусы качения колес в ведомом режиме зависят от исходных размеров шин, давления воздуха в шинах и вертикальной нагрузки на колесах. Проф. Г. А. Смирнов предложил формулу для определения радиуса качения в ведомом режиме в зависимости от вертикальной нагрузки Р,-:

Зго-(2Я,/С )

где Го - свободный радиус колеса.

Приведенная формула предполагает обратную пропорциональность Гв от Ри что подтверждается экспериментально.

Эксперименты также показали, что свободные радиусы колес при одинаковом давлении воздуха в шинах оказываются неодинаковыми. Их разность приблизительно такая же и в ведомом режиме, в случае одинаковой вертикальной нагрузки на колесах, хотя абсолютная величина радиусов качения за счет вертикальной нагрузки будет меньше. Разность радиусов качения Гв колеблется в пределах допуска на изготовление шин и в зависимости от размера колес составляет 8. ..15 мм. Максимальная величина кинематического несоответствия будет достигать 1,5. ..2%-

В некоторых конструкциях автомобилей предусмотрено разное давление воздуха в шинах передних и задних колес. Перепад давлений для различных автомобилей колеблется в пределах 40. ..150 кПа. Это приводит к разности свободных радиусов колес 4. ..10 мм, что вызывает кинематическое несоответствие 1...1,5%. Современные многоосные автомобили высокой проходимости снабжаются, как правило, центральной системой регулирования давления воздуха в шииах, поэтому разность радиусов колес, обусловленная перепадом давления, не возникает.

Распределение силы тяжести по осям зависит от схемы их расположения по базе и положения центра масс. Вертикальные нагрузки на сближенных осях (осях тележек) незначительно различаются между собой, а при балансирной подвеске практически одинаковы (см. гл. 3), поэтому кинематическое несоответствие между осями тележки по этим причинам не возникает. Разница нагрузок на разнесенные оси может колебаться в широких пределах как статических, обусловленных положением центра масс, так и в динамических, возникающих вследствие продольно-угловых колебаний автомобиля и действия продольных сил. Между осями будет возникать кинематическое несоответствие в результате действия разных вертикальных нагрузок. Наибольшая неравномерность вертикальных нагрузок характерна для автомобилей без груза. Максимальная разность нагрузок на колесах разнесенных осей в этом случае достигает 20 кН и более. Это вызывает разность радиусов качения колес до 10 мм и кинематическое несоответствие 1...1,5%.