временный характер и в зависимости от скорости движения продолжается 0,2.. .0,8 с;

характер изменения несоответствия для многоосных автомобилей при движении по препятствиям, имеющим высоту больше полного хода подвески, может меняться, если будет происходить значительное перераспределение нагрузок между колесами и осями, рассмотренное в гл. 3.

Обобщенное максимальное значение возможного кинематического несоответствия (в %) современных многоосных автомобилей приведено ниже.

Таким образом, кинематический анализ на первом этапе исследования работы трансмиссии дает очень много данных. На основании только этого анализа можно определить замкнутые контуры силового потока с наибольшим кинематическим несоответствием, в которых необходимо иметь РУТ. На основе полученных данных применительно ко всем типам автомобилей можно утверждать, что наибольшее кинематическое несоответствие возникает при криволинейном движении в замкнутом контуре колес левой и правой сторон автомобиля. Поскольку криволинейное движение - основной вид движения автомобиля, то кинематическое несоответствие будет постоянно действующим, и для его устранения в указанных контурах необходимо устанавливать РУТ. Следует отметить, что различных мнений по установке межколесных развязывающих механизмов нет, на всех автомобилях такие механизмы (различного типа) устанавливают.

Таких же значений кинематическое несоответствие достигает между осями у автомобиля только с передними управляемыми колесами, главным образом между управляемыми осями и между управляемой и неуправляемой осями. Очевидно, по аналогии с предыдущим в этих контурах также необходимо устанавливать развязывающие механизмы.

Другой группой причин, вызывающих на всех типах автомобилей большие кинематические несоответствия, являются макронеровности и изменение вертикальных нагрузок на колесах в динамике. Эти условия вызывают появление переменного во времени кинематического несоответствия.

26. СИЛОВОЙ АНАЛИЗ ИДЕАЛЬНОГО СИЛОВОГО ПОТОКА

Метод полного исследования силового потока трансмиссии многоосного автомобиля впервые разработал А. С. Антонов. Им предложены общие уравнения для определения сил тяги на колесах при прямолинейном и криволинейном движениях, дан анализ условий возникновения циркулирующей мощности на основе разных свободных радиусов колес. Ниже для удобства сопоставления расчетных и экспериментальных данных, когда замеряются крутящие моменты (а не силы тяги) и соответствующие коэффициенты, и для учета суммарного кинематического несоответствия, действующего в замкнутых контурах трансмиссии реальных автомобилей, приводится метод силового анализа идеального силового потока на базе исследования распределения крутящих моментов. Предлагаемый метод не противоречит методу А. С. Антонова, несколько уточняя и дополняя последний.

При исследовании распределения мощностей по колесам в различных схемах силового потока в качестве основного допущения принято, что крутящие моменты в приводе к колесам переменные, но изменяются с малыми ускорениями. Это дает право не учитывать инерционные моменты, что при оценке и выборе различных схем трансмиссий возможно. Установлено, что различные схемы трансмиссий главным образом влияют на средние величины моментов и на моменты, изменяющиеся с малой частотой. Средние моменты и соответствующие им окружные силы определяют тягово-сцепные свойства, устой)ивость и управляемость автомобиля.

Переменная динамическая составляющая момента, ее амплитуда и частота колебаний являются характеристикой динамической нагруженности по условиям усталостной прочности. При исследовании этих вопросов она и должна изучаться. Принятая схема трансмиссии при этом оказывает малое влияние.

Составим расчетную схему силового потока трансмиссии п-осного автомобиля. Принимаем, что момент, подводимый от двигателя к колесам, является известным и определяется внешними условиями движения и внешними сопротивлениями, которые также известны.

При инженерных расчетах трансмиссии многоосного автомобиля подводимый момент для случая установившегося прямолинейного движения по ровной дороге может быть определен по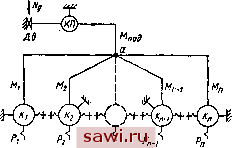

известной зависимости тяговых расчетов автомобиля

Рис. 48. Расчетная схема силового потока

где Ga - сила тяжести автомобиля; fo - табличное значение коэффициента сопротивления качению данного автомобиля; Гк - расчетный радиус качения.

При криволинейном движении этот крутящий момент должен быть увеличен в 2... 4 раза в зависимости от типа привода. Большее увеличение берется для блокированного привода, меньшее - для дифференциального. К этому следует еще добавить крутящий момент, необходимый для преодоления сопротивления воздуха, если движение происходит с большими скоростями. Принимаем, что потери в трансмиссии отсутствуют.

Принятые допущения исследования распределения мощностей по колесам позволяют применить упрощенную схему силового потока. Поскольку режим движения по внешним сопротивлениям задан, будет заданным и режим работы многих механизмов и устройств трансмиссии (коробки передач, раздаточной коробки и др.), поэтому на схеме силового потока их можно изобразить в виде разветвляющихся точек или направленных потоков. Эта особенность теории силового потока значительно упрощает проведение исследований, не искажая физического смысла явлений.

К исследованию примем одну сторону автомобиля с блокированной связью в замкнутых контурах, в которых задано суммарное кинематическое несоответствие, рассчитанное по методам, приведенным в разд. 25. Расчетная схема силового потока изображена на рис. 48. Буквой а обозначена разветвляющаяся узловая точка, показано направление и обозначен момент Мпод, подведенный в трансмиссию от двигателя Дв, равный моменту внешних сопротивлений. Искомые крутящие моменты на колесах обозначены Mi.. .Мп, направление их пока неизвестно.

Колеса и мосты рамой соединены в единую систему. Поэтому поступательные скорости центров всех колес одинаковы и угловые скорости колес равны. В связи с этим имеющееся кинематическое несоответствие в каждом контуре должно быть компенсировано за счет упругого или абсолютного скольжения. Необходимость скольжения приведет к появлению в каждом замкнутом контуре упругого момента, который равен при любом режиме движения разности моментов на колесах контура: 146

AM2i = M2-Mi; ДЛ1з1 = Мз-М1;

Получим п-1 уравнений упругости. В принципе уравнения можно составлять для любого сочетания контуров, исключая равнозначные.

На основании второго принципа теории силового потока для разветвляющейся узловой точки а (см. рис. 48) можно записать

M o,==Mi-fM2-fM3+... + f i + M . (51)

Используя систему уравнений (50)и уравнение (51), - получим выражения для определения моментов, подведенных к колесам:

Для решения этой системы необходимо определить упругий момент в контуре. Рассмотрим работу одного контура. Упругий момент в контуре на основании уравнения (42) зависит от геометрической связи и приведенной податливости контура. Геометрической связью является суммарное кинематическое несоответствие Sm* в контуре, а приведенная податливость определяется тангенциальной эластичностью шины и грунта, обусловливаемой изменением радиуса качения колеса на единицу (1 кН-м) подводимого к колесу крутящего момента. Податливость механической части привода колеса не учитываем. Исследования показали, что податливость привода влияет в неустановившемся режиме до момента, пока не вступило в действие выравнивающее свойство эластичных шин. Сравнительно небольшая разница жесткостей валов привода на реальных автомобилях не вызывает существенного перераспределения моментов даже при трогании автомобиля с места.

По зависимости акад. Е. А. Чудакова можно записать

Для колес одного контура из-за жесткой их связи с рамой и одинаковых угловых скоростей

к1 = -к2, Т. е. r,i3-Y piA/i=--r,2B-Yni.22- (5Э)

в общем случае Vnpi=7v p2, так как тангенциальная эластичность шин и плотность грунта под колесами различны. Обозначим Ynp2/Ynpi = ; Vnp2 = Ynpi, тогда выражение (53) примет вид

Ш2-Ж1 = (г,2з-Г,1з)/у р1 = ДГ,.,/у р1, (54)

Кроме того, для разветвляющей точки любого контура (см. рис. 48)

Af2 + Afi = Af i2. (55)

где Маолп - момент, подведенный к контуру /. Решая совместно уравнения (50), (54) и (55), получим

дуй,

Заменяя разность радиусов в ведомом режиме через кинемати--ческое несоответствие из формулы (44) при Ыт = Мк, окончательно получим выражение для упругого момента в контуре

Х21Г2В

50Упр1 ( + 1) * -Ы

При равенстве приведенной тангенциальной эластичности шин и грунта, когда k-=\, формула упругого момента примет вид

А?21 = Х21-2в/(100Упр). (57)

В общем виде

\ткГп.

Ams=X ft-B/(100Y p). (58)

Полученные выражения показывают, что в пределах упругого скольжения упругий момент в замкнутом контуре зависит от кинематического несоответствия, приведенной тангенциальной эластичности шины и грунта, соотношения податливостей под колесами контура и от подведенного к контуру крутящего момента.

Интересно отметить, что при разной приведенной тангенциальной эластичности упругий момент может возникать в контуре при отсутствии кинематического несоответствия, и в данном случае он зависит от момента, подведенного к контуру. Это значит, что на разность моментов в замкнутом контуре влияют два

фактора - кинематическое несоответствие и разная тангенциальная эластичность колес и грунта. Отмеченное обстоятельство имеет важное значение для исследования проходимости колесных машин по деформируемым грунтам. Податливость такого грунта под передними колесами значительно отличается от его податливости под колесами, идущими по следу. Поэтому выбор оптимального значения момента, подводимого к различным колесам с учетом разной податливости грунта, может дать определенный эффект по повышению проходимости автомобиля.

Указанные зависимости применимы и для контура, образованного ведущими мостами с дифференциальной связью между колесами. Для этого необходимо подставлять величины, относящиеся к мостам, а именно:

приведенный радиус качения в ведомом режиме дифферен-

циальной оси г в=-°-;

к.л.в Ь к.п.в

приведенную тангенциальную податливость моста 7пр.м= =Тпр/2.

Кинематическое несоответствие должно быть подсчитано для межосевого контура.

На основе полученных зависимостей проведем анализ характера распределения моментов и условия возникновения циркулирующей мощности применительно к одному замкнутому контуру, что соответствует двухосному полноприводному автомобилю или двум осям многоосного автомобиля. По уравнениям (52) и (57) моменты на колесах:

100Л1 олУпрг-Х21Г2в

2- IOO-V

100Л? одУпр +Х21Г2В

2.100упр

(59)

Циркуляция мощности будет отсутствовать, если моменты

Ml и М.Ч положительны, при этом -1<Х212в/(1007пр.Мпод)<1,

т. е. условие бесциркуляционной работы контура запишется

Х21Г2 /(100УпР од)< 1-

(60)

Из формулы следует, что циркуляция мощности зависит от суммарного кинематического рассогласования работы контура, приведенной тангенциальной эластичности шин и грунта и внешнего сопротивления движению автомобиля. Полученное условие совпадает с результатами, полученными ранее проф. А. С. Антоновым [3] другими методами. Зависимость несколько уточняет условия бесциркуляционной работы. Уточнение состоит в том, что циркуляция мощности может возникнуть и при равенстве свободных радиусов колес. Наличие разности свободных радиу-