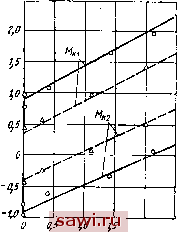СОВ не является обязательным условием возникновения циркуляции мощности.

Из зависимости (60) можно установить, что допустимость применения в схеме трансмиссии замкнутого блокированного привода в первую очередь определяется величиной часто встречающегося кинематического несоответствия и тангенциальной эластичностью шин, а также условиями работы автомобиля, которые влияют на приведенную эластичность и на подводимый в контур момент, определяемый внешними сопротивлениями.

На рис. 49 показаны результаты расчета (прямые линии) и экспериментальной проверки (точки) распределения крутящих моментов по ведущим осям автомобиля при различном суммарном кинематическом рассогласовании и внешнем сопротивлении. Суммарное рассогласование задавалось различным давлением в шинах, свободным радиусом качения и криволинейным движением, внешнее сопротивление-нагрузкой на крюке. График подтверждает правомерность и достаточную точность принятой методики расчета. Разработанные методы могут быть проверены экспериментально.

Из рисунка видно, что разность моментов на осях при постоянных Ynp зависит от суммарного кинематического несоответствия и не зависит от подводимого общего момента. Циркуляция мощности зависит от М од и %.

Ниже на рисунках представлены результаты обработки опытов в части выявления связи распределения крутящих моментов с давлением в шинах и с радиусом поворота автомобиля.

На рис. 50 отражены результаты измерения крутящих моментов на колесах первой и второй осей с блокированным приводом в зависимости от перепада давлений воздуха в шинах Арш. При эксперименте давление воздуха в шинах колес первой оси поддерживалось постоянным, рш=350 кПа, а в шинах колес второй оси изменялось. На графике приведена также расчетная зависимость % от перепада давлений. Кинематическое несоответствие X определялось по результатам измерения радиусов каче-

Рнс. 49. Расчетно-экспернмен-тальная зависимость распределения по ведущим осям подведенного момента при различном кинематическом несоответствии:

--Х . = 3,27%:-----

-1,33%

ния в ведомом режиме с отключением их от трансмиссии. Все опыты проводились на ровной бетонной дороге.

На рис. 51 приведены результаты измерения крутящих моментов на колесах первой и второй осей при криволинейном движении того же автомобиля в зависимости от радиуса поворота по колее переднего наружного колеса. Эксперименты проводились на бетонной площадке при движении автомобиля по кругу заданного радиуса со скоростью 5 км/ч. Величина xzi определялась по результатам измерения радиусов траекторий движения отдельных колес по отпечаткам шин на дороге.

Приведенные графики показывают, что характер воздействия кинематического несоответствия на работу блокированного привода остается одинаковым независимо от причины возникновения кинематического несоответствия.

С ростом значения х увеличивается разность между крутящими моментами на колесах, а на одной из осей возникает отрицательный момент, т. е. появляется циркулирующая мощность. Отрицательный момент будет тем больше, чем больше %.

Для экспериментального автомобиля при движeии по бетону при сравнительно небольшом х=~3,27% для ликвидации циркуляции мощности необходим приведенный момент внешнего сопротивления более 2 кН-м. Реальное внешнее сопротивление по экспериментальным данным (момент приведен к раздаточной

х;/о

О 50 100 750Лрш,кЛа

Мк,кН-м

so R,M

Рнс. 50. Изменение кинематического несоответствия и распределения крутящих моментов в завнснмостн от перепада давления воздуха в шинах

Рис. 51. Изменение кинематического несоответствия н распределения крутящих моментов в завнснмостн от радиуса поворота

коробке) составляет: на бетонной дороге 0,20.. .0,40 кН-м, на сухой грунтовой дороге 0,70.. .0,90 кН м, на песке 0,90... 1,5 кН м. Это означает, что при данном % в контуре ведущих мостов практически всегда будет циркулировать мощность, и блокирование привода недопустимо.

В приводе помимо циркулирующей мощности недопустима также большая разница моментов, так как в этом случае одна ось (колесо) будет перегружена, а другая недогружена, что отрицательно сказывается на тягово-сцепных качествах, проходимости, экономичности автомобиля и надежности привода.

Практическое применение методов расчета проиллюстрируем следующим примером.

Автомобиль типа 8X8 имеет блокированный привод колес каждой стороны от автономного двигателя. Определим распределение момента двигателя при движении автомобиля на повороте по колесам наружной (относительно центра поворота) стороны. Исходные данные: число колес блокированного привода п=4; коэффициент тангенциальной эластичности шин v = = 7,6 мм/(кН-м); Г1в = 628 мм; Г2в = 630 мм; Гзв=631 ММ; Г4в = 630 мм. Радиусы траекторий движения колес соответственно:

/?1 = /?4= 12,5 м; /?2 = Лз= 12,1 м. Тогда X конструктивно-эксплуатационного происхождения:

X2\ =

j 100% =0,3%;

,100% = 0,5%; 631 /

(l-)-100% =0,3%;

1 -1-

2)100%

X криволниейиого движения:

2i = (-j--l) 100%=3,3%;

хз1 = Х21 = з,з%: х41 = о.

Суммарные значения:

2X21 = 3,6%; 2X31 = 3,8%; 2 = 0,3%.

Принимая крутящий момент коленчатого вала двигателя, приведенный к выходному валу колесного редуктора, Л1под= 4 кН-м, определим упругие моменты по формуле (58):

ДЛ121 =

ДЛ145 =

= 2,98 кНм; = 3,16 кН-м; = 0,25 кН-м.

По формулам (52) находим крутящие моменты на колесах: Afi = -0,60 кН-м; /И2 = 2,38 кН-м; А1з = 2,56 кН-м; Л14 =-0,35 кН-м.

Приведенный расчет наглядно показывает характер работы трансмиссии в данных условиях движения.

Для инженерных методов тягового расчета формулы (59) можно преобразовать в силовом выражении и привести к виду

Pi = 0,5P, -x2i/(2Ynp); Я2 = 0,5Я, +Х2,/(2упр), -(61)

где Реп -общая сила сопротивления движению контура; Pi и Рг - силы тяги на колесах (осях).

Выше рассмотрена работа трансмиссии при равной тангенциальной эластичности колес, что характерно для автомобилей, имеющих на всех осях одинаковые шины, и для случая движения колесных машин по твердым покрытиям и грунтовым дорогам. Как уже отмечалось, при движении по деформируемым грунтам часто 1ар\Фуап- Рассмотрим этот режим работы трансмиссии. По зависимостям (52) и (56) определим моменты на колесах:

100М одУ р1 - Х21Г2В

100Y pi(*-f 1)

00ЛподУ..р1(2-) +Х21Г2В lOOYnpi {k + \)

(62)

Сравнивая полученные зависимости с формулами (59), видим, что они имеют ту же структуру и дополнительную величину k, характеризующую отношение эластичностей. Следовательно, дополнительно к отмеченным ранее факторам здесь на распределение моментов и циркуляцию мощности будет влиять и это соотношение. Примем, что в контуре кинематического несоответствия нет,т. е.х21 = 0, тогда М1=М од/(й+ 1); М2=М од(2- -k)l(k->r\), а отношение моментов на колесах Mi/M2=l/(2-k).

Из полученной зависимости можно сделать следующие выводы. При движении по деформируемым грунтам, когда тангенциальная эластичность переднего колеса (оси) больше, чем второго (й<1), при полном кинематическом соответствии на переднем колесе (оси) момент будет меньше, чем на втором колесе (оси). Переднее колесо может оказаться недогруженным по его сцепным возможностям, а заднее колесо (ось) - перегружённым. Тягово-сцепные возможности автомобиля будут недоиспользованы, проходимость снижена. Для выравнивания моментов по колесам (осям) на основании уравнений (62) необходимо искусственно в контуре создать определенное отрицательное кинематическое несоответствие.

Этот вывод дает объяснение того, что на некоторых колесных тракторах для повышения тяговых качеств искусственно в привод ведущих колес вводят кинематическое несоответствие. В результате этого на определенных грунтах удавалось увеличить тягу на крюке до 30%. При это.м возникает проблема изучения необходимого оптимального распределения моментов по колесам при движении колесных машин по деформируемым грунтам с целью повышения их проходимости. Для этого в первую очередь необходимо теоретически и экспериментально исследовать приведенную тагенциальную эластичность шин при работе их на различных реальных грунтах, которая, как показывает опыт, зависит от многих факторов [2].

27. СИЛОВОЙ ПОТОК В ТРАНСМИССИИ ПРИ ТОРМОЖЕНИИ

Представляет теоретический и практический интерес рассмотреть идеальный силовой поток в трансмиссии многоосного автомобиля при его торможении и установить влияние схемы трансмиссии на тормозные свойства. В настоящее время общепринято при исследовании тормозных свойств автомобиля влияние трансмиссии на перераспределение тормозной мощности по колесам не учитывать. При рассмотрении двухосных и неполиоприводных автомобилей это допущение не оказывает существенного влияния, для многоосных автомобилей, как будет показано ниже, оно неприемлемо.

При торможении любого автомобиля очень трудно оптимизировать подводимый к каждому колесу тормозной момент. Всегда имеет место неравенство моментов на различных колесах, которое на многоосных автомобилях усиливается из-за большой протяженности тормозного привода.

Сложная связь через трансмиссию между отдельными колесами и мостами существенно перераспределяет тормозные моменты в зависимости от принятой схемы трансмиссии. Для установления закономерностей перераспределения тормозных моментов рассмотрим силовые потоки в элементах трансмиссии одного замкнутого силового контура, приняв следующие допущения: торможение присходит под действием одного колесного тормозного механизма, что наиболее наглядно характеризует возможную неравномерность тормозных моментов на колесах; двигатель не разъединен с трансмиссией и он влияет на процесс торможения.

Рассмотрим два типа замкнутых контуров - блокированный и дифференциальный с симметричным дифференциалом. С учетом принятых условий и требований теории силового потока [3] на рис. 52 показаны схемы силовых потоков двух контуров. На схемах приняты обозначения: ki и k2 - узловые точки колес контура; Тр1 и Тр2 -колесные тормозные механизмы (Tpi включен);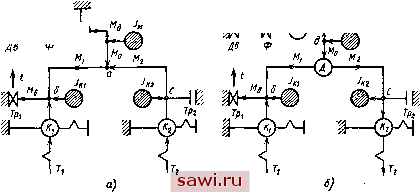

Рис. 52. Схема силового потока контура трансмиссии при торможении; а - блокированный привод; 6 - дифференциальный привод

/м И / - обозначают инерционные узловые точки силового, потока, в которых осуществляется подвод кинетической энергии, появляющейся при торможении от вращающихся элементов трансмиссии и колес. Стрелками показаны направления силовых потоков при данном режиме торможения в данной схеме трансмиссии. Стрелками с символом / обозначена отводимая от узловых точек рассеиваемая тепловая энергия. Остальные обозначения соответствуют принятым на рис. 44, 45.

Представленные схемы силовых потоков иллюстрируют физическую сущность происходящих процессов и направления силовых потоков при торможении, осуществляемом тормозным механизмом, одного колеса и двигателем.

При блокированном приводе колес (рис. 52, а) включенный тормозной механизм создает тормозные силы на всех колесах силового контура и поглощает кинетическую энергию колес и часть кинетической энергии вращающихся масс трансмиссии. Остальную часть гасит двигатель, работающий в режиме торможения. Возможно в определенный момент часть тормозной энергии колес будет гасить двигатель. Таким образом, блокированный привод трансмиссии обеспечивает явно выраженное выравнивание тормозного момента по колесам и, следовательно, выравнивание тормозных сил в контакте колеса с дорогой Т\ и Тг (см. рис. 52, а).

При дифференциальном приводе (рис. 52, б) картина силового потока в трансмиссии совершенно иная. Тормозной механизм колеса К\ обеспечивает торможение только этого колеса и поглощает часть кинетической энергии трансмиссии и тормозящего колеса. Для колеса Ki сохраняется тяговая сила Тг и происходит процесс накопления кинетической энергии колеса, так