как дифференциал, как РУТ контура, только разветвляет силовой поток, распределяя его поровну по колесам. Следовательно, в дифференциальном приводе при торможении никакого выравнивания тормозных сил не происходит. Наоборот, на колесах появляются тангенциальные силы, различные по направлению, которые создают поворачивающий, дестабилизирующий момент, нарушающий устойчивость движения автомобиля. Дифференциал выполняет функции механизма поворота.

Такова качественная картина силового потока работы трансмиссии при торможении. Для получения количественных зависимостей необходимо математическое описание расчетных схем силового потока. Приведенные уравнения (52) для решения данной задачи не годятся, так как требуется рассмотреть неустановившийся режим работы трансмиссии.

На основании принципов теории силового потока составим дифференциальное уравнение изменения силовых факторов, приняв в качестве расчетной схемы (см. рис. 52, а).

Из условия динамического равновесия разветвляющих узловых точек а, б я д можно записать:

(63)

где ию Wm - угловые скорости соответственно колеса и инерционной узловой точки (точка д рис. 52, а).

Знаки членов уравнений принимаются в соответствии со схемой силового потока.

В указанных уравнениях в качестве задающего параметра можно принять тормозной момент на барабане колеса Мб. Для определения тангенциальных сил необходимо знать тормозной момент двигателя Л1д и инерционный момент трансмиссии /мсом, определение которых связано с большими трудностями. В связи с этим для решения поставленной задачи примем дополнительные допущения и упрощения. Будем рассматривать процесс торможения с отсоединенным от трансмиссии двигателем, т. е. Л1д=0, и заменим инерционный момент вращающихся частей трансмиссии суммой упругих моментов в контуре, определяемой податливостью механической части привода колес: Уии =

=2 -п/ упругий момент привода колеса М ~к(а)к-

- мЛ - коэффициент жесткости контура, который при расчетах будем принимать равным угловой жесткости полуосей автомобиля в пределах 50...80 кН-м/рад.

Упругий момент, обусловленный кинематическим несоответствием в контуре при данном неустановившемся режиме работы не учитываем.

При принятых допущениях на основании уравнений (63) для блокированного контура можно записать

для дифференциального контура с симметричным дифференциалом

Л%=6 - Ji - 0,5М ;

yW =Ka [0,5 (%,Ч- к2)- м1-

Н. М. Назаровым предложена методика решения и проведен расчет этих дифференциальных уравнений с помощью АВМ. На рис. 53 приведена принципиальная схема набора задачи на АВМ для случая блокированной трансмиссии. Переход к другим трансмиссиям осуществляется изменением коэффициентов передачи по соответствующим входам операционных усилителей. С помощью нелинейного блока сила 7 ,- ограничивается величиной Тсщ, предельно возможной по условию сцепления колеса с дорогой. Начальные условия для сок и сом выбирают одинаковыми в соответствии с начальной скоростью продольного движения автомобиля Ux. Кроме того, в схему обратной связи интегрирующих усилителей, формирующих значения сок,-, включены диоды, что позволяет фиксировать изменение сок/ в положительных значениях до нуля (момента блокировки) и обеспечивает мгновенное разблокирование колес при снятии тормозного момента на барабане.

В качестве примера решаемых с помощью разработанной методики задач ниже приведены результаты расчета изменения тормозных сил на колесах автомобиля Урал-375Д , имеющего различные схемы трансмиссии при торможении переднего левого колеса на сухой и скользкой дорогах (рис. 54 и 55). Первой цифре индекса в обозначении силы Т иа рисунках соответствует порядковый номер моста, второй - принадлежность к левой (индекс /) или правой (индекс 2) стороне автомобиля.

При дифференциальной р принципиальная схема набо-трансмиссии (рис . 54, а и б) рд решения задачи на АВМ для бло-ПОДВОДИМЫЙ к колесу тормоз- кированного контура

М ;----

3]Н>

ной момент Мб реализуется в контакте колеса с дорогой и иа другие колеса не передается, при этом тормозящееся колесо может потерять сцепление с дорогой и заблокироваться. Поворачивающий момент ЛГпов, действующий на автомобиль и представляющий сумму моментов тангенциальных сил относительно проекции центра масс автомобиля на дорогу, равен произведению тангенциальной реакции тормозящегося колеса на половину колеи.

При полностью блокированной трансмиссии (рис. 54, виг) развиваемый на колесе тормозной момент равномерно распределяется на все колеса автомобиля, а поворачивающий момент равен нулю. Все колеса автомобиля блокируются одновременно несмотря на то, что терять сцепление с дорогой могут раньше колеса с меньшими нормальными реакциями.

6 Mf,KHn

0 If 8 Mf,KH-n

6 t1f,KHn

20 Ms,kH-

Рис. 54. Распределение тормозных сил при дифференциальной и блокированной трансмиссии:

о в б-соответственно на сухой ((р=0,7) н скользкой (ф=.о,2) дороге при дифференциальной трансмксскк; в и г - то же, прн блокированной трансмнсснн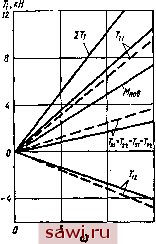

М ов, кН-м 21*

6 М{,кИ-н

и 8 Ме,кн-м

Рис. 55. Распределение тормозных сил при частично блокированной трансмиссии:

в -сухая дорога (Ф-0,7); б - кользкая дорМа (Ф=0,2)

Частично блокированной трансмиссией назовем трансмиссию, у которой привод мостов блокированный, а привод колес в мостах дифференциальный.

В этом случае (см. рис. 55) в контакте тормозящегося колеса с дорогой реализуется 65...67% момента Мб, а на колесах других мостов - 16...17%. На втором колесе того же моста появляется сила тяги, составляющая 29...33% тормозного момента, отнесенного к радиусу колеса. При этом алгебраическая сумма тангенциальных сил на колесах всех мостов, развивающих тормозные усилия, составляет МъЦЗгк), а поворачивающий момент Маов=МбВ1(2гк) (В - колея автомобиля). Указанные соотношения тангенциальных реакций в контакте колес с дорогой остаются неизменными до момента достижения на тормозящемся колесе предельных по условиям сцепления значений. При дальнейшем увеличении момента Мб увеличиваются сила тяги во втором колесе того же моста и поворачивающий момент, а тангенциальная реакция на тормозящемся колесе остается неизменной.

При достижении предела по сцеплению на тяговом колесе (точка К) тормозящееся колесо блокируется, а тяговое колесо на основании свойств дифференциала начинает вращаться с угловой скоростью, в 2 раза большей, чем скорость колес других мостов. Поворачивающий момент достигает предельного значения. При дальнейшем увеличении момента М никаких изменений в процессе торможения автомобиля не происходит. Следует заметить, что характер распределения тормозных сил отличен

от приведенного при другом количестве тормозящихся колес и другой интенсивности их торможения.

Изменяется количественная характеристика рассматриваем мых параметров, но закономерности изменения качественной стороны процесса торможения сохраняются.

Экспериментальная проверка разработанной математической модели и достоверности полученных с ее помощью результатов проводилась испытанием автомобиля Урал-375Д на трехосном барабанном стенде. Экспериментальные данные по распределен нию тормозных сил по колесам автомобиля с дифференциальной и частично блокированной трансмиссиями при торможении одним колесом приведены на рис. 54 и 55 (штриховые линии). На рисунках видно, что результаты расчетных и экспериментальных исследований полностью согласуются качественно и с достаточной для практики точностью количественно, что подтверждает правомерность принятых при создании математической модели допущений и возможность ее использования при проведении аналогичных исследований.

Таким образом, приведенные выше материалы показали, что исследование и оценку тормозных свойств многоосных автомобилей необходимо проводить с учетом закономерностей распределения тормозных сил по колесам в зависимости от схемы установленной на автомобиле трансмиссии.

Рассмотренная методика расчета трансмиссии на базе теории силового потока позволяет определить очередность потери сцепления и блокировки колес в процессе нарастания давления в тормозном приводе, изменение суммарной тормозной силы ST; в контакте всех колес с дорогой, а также определить поворачивающий момент Миов, действующий на автомобиль, п оценить устойчивость автомобиля при тормоясении.

Установленные закономерности влияния типа трансмиссии на распределение тангенциальных сил при торможении по колесам следует учитывать при формировании независимых контуров тормозного привода.

При дифференциальной или частично блокированной трансмиссиях применение диагонального или полудиагональпого разделения тормозного привода на контуры недопустимо. В этом случае возможно появление больших дестабилизирующих моментов, действующих на автомобиль при выходе из строя одного из контуров, и исключается возможность использования сил сцепления нетормозных колес с опорной поверхностью для торможения.

28. АНАЛИЗ ПОТЕРЬ & ТРАНСМИССИИ НА ОСНОВАНИИ ДИССИПАТИВНЫХ ФУНКЦИЙ СИЛОВОГО ПОТОКА

По приведенным выше данным и методике можно оценить схему трансмиссии с точки зрения распределения мощностей по

колесам, определить необходимые места установки РУТ. Для определения целесообразного типа механизмов РУТ и для экономической оценки работы данной схемы трансмиссии и ее связи с общей схемой автомобиля необходимо проведение исследований потерь мощности. Для этого требуется полная схема силового потока с обозначением направлений всех потоков мощности и их величин, определенных по зависимостям, приведенным в подразд. 25 и 26.

В соответствии с общей теорией силового потока для решения поставленной задачи необходимо для каждой узловой точки силового потока знать диссипативные функции, отображающие закономерности диссипативных потоков. Указанные функции могут быть заданы в любом виде - таблицами, графиками или аналитически.

Для проведения анализа потерь все узловые точки силового потока целесообразно разбить на три группы: немеханические (индекс Н), механические (индекс М) и обобщенные точки колес. Тогда общая мощность потерь в трансмиссии

1 1 1

к немеханическим узловым точкам прежде всего относится двигатель, а также немеханические трансформаторы (электрические, гидродинамические и др.). Потери в этих точках (их дис-сипативная функция) обычно задаются графически на основании стендовых испытаний. Эти функции считаем заданными и анализировать их не будем, отметим только, что их роль в общих потерях велика и зависит от режима нагружения. Учитывать потери в рассматриваемых точках, вводя в расчет среднее значение КПД, ошибочно, применяя предельное значение КПД также не совсем правильно [3].

Надежных способов определения потерь с учетом различных режимов работы механизмов пока нет. Можно пользоваться эм-мирической формулой, предложенной И. Н. Корнилаевым [3]:

где а, р, fe, m - опытные коэффициенты, зависящие от типа зубчатого зацепления и вида смазки механизма; Np - потери в полюсе зацепления; Vp - относительная окружная скорость колеса в полюсе зацепления, м/с; N - относительный мощностной фактор потока, проходящего через полюс зацепления.

Формула показывает, что потери в механических узловых точках зависят от числа пар полюсов зацепления зубчатых колес,

1И дает возможность определить потери в механизмах, работаю-

1:Щих вхолостую и с частичной нагрузкой.

Потери в механических узловых точках имеют большое зна-