автомобиля боковой силой происходит плавно, с нарастанием угла бокового крена без ускорения. В особых условиях нагруже-ние боковой силой может происходить динамически, крен системы в этом случае происходит с ускорением, кинетическая энергия возрастает. Эта энергия расходуется на дополнительную деформацию автомобиля в поперечной плоскости.

Движение системы при динамическом крене может быть представлено дифференциальным уравнением (см. рис. 74)

У;р = 7Я-р(С,-0зЯ), (75)

где /э - момент инерции системы в поперечной плоскости. Уравнение (75) относительно р имеет решение в виде

-С1ехраЛ/)--С2ехр(-1Л/)=

-fCjCos Л-f-C4siп At,

где Л= )/(Су-Оа/)Ур Ci, Сг, Сз, С4-постоянные интегрирования; t - время.

Постоянные интегрирования из начальных условий, когда /=0; р = 0 и р=0;

тогда

1- cos

(76)

Определив экстремальное значение функции (76) по максимуму, с учетом уравнения (73), показывающего статическое изменение угла крена, получим

Рдтах/Рс max = 2.

Это означает, что аварийный угол крена в 2 раза больше его статического значения при воздействии одной и той же опрокидывающей силы. Для реальных автомобилей это соотношение несколько меньше двух, поскольку расчетное значение получено без учета нелинейности боковой приведенной жесткости кренящейся системы, неупругого сопротивления и силы трения, которые имеют место в реальных условиях опрокидывания автомобилей.

При инженерных приближенных расчетах с учетом запаса по устойчивости можно считать, что динамический угол крена не должен превосходить статический более чем в 2 раза. Например, угол наклона косогора, по которому может уверенно двигаться автомобиль без опрокидывания, должен быть не более

половины статического угла устойчивости, определенного на

стенде опрокидывания.

Опрокидывание на деформируемых грунтах является особым опасным случаем потери устойчивости и характерным для некоторых многоосных автомобилей. У обычных автомобилей такое явление наблюдается редко.

Опрокидывание чаще всего происходит при съезде многоосного автомобиля с высоким расположением центра масс и большими нагрузками на ось (более 100 кН) одной стороной на обочину дороги, имеющей низкую несущую способность грунта н неукрепленные откосы. При этом из-за больших осевых нагрузок колеса одной стороны, находящиеся на обочине, прорезают глубокую колею, происходит сползание грунта и автомобиль с грузом опрокидывается вследствие крена подрессоренной массы на мгновенно образовавшемся косогоре , превышающем допустимую крутизну. Опрокидывание происходит, как правило, быстро и часто бывает трудно принять какие-либо меры по его предотвращению.

В рассматриваемом случае условие устойчивого движения по опрокидыванию можно записать:

Я -Яз<5siпf. (77)

Из выражения (77) следует, что опрокидывание автомобиля зависит не только от угла статической устойчивости ф, но также н от разности глубин образуемой колеи с наружной (по отношению оси дороги) Я и внутренней Яв сторон автомобиля.

Глубина образуемой колеи находится в сложной зависимости от параметров грунта и характеристик шины, нагрузки на колесо, числа проходов по одному следу и др. Для оценки устойчивости на деформируемом грунте предложена номограмма, построенная на основе расчета опрокидывания автомобиля при образовании различной по глубине колеи в зависимости от состояния грунта. По номограмме (рис. 76) графоаналитическим методом можно определить допустимую несущую способность обочины дороги, исключающую опрокидывание. Номограмма строится для каждого многоосного автомобиля, для которого существует опасность опрокидывания на деформируемых грунтах.

На рис. 76 в первом и третьем квадрантах изображены семейства кривых изменения образуемой колеи с каждой стороны автомобиля на различных грунтах, характеризуемых параметрами Сг и ц [1, 16].

Кривые построены по зависимости, связывающей нагрузку на колесо Gk с образуемой колеей Як [16],

Ок=сАУ(1-!/3)ЯГ°,

где Сг и ц -параметры деформируемого грунта; 6к - ширина шины колеса, см; Гж==Гк(1-ЬЛг/Л) - радиус жесткого колеса,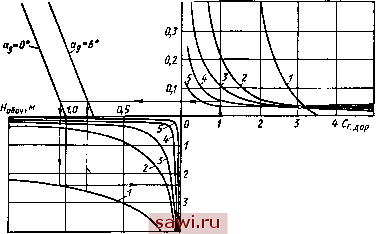

Рис. 76. Номограмма оценки условий устойчивости на деформируемых грунтах при различных значениях ц:

/ - 0; 2 - 0,25; 3 - 0,5; 4 - 1; 5-2

эквивалентного по кривизне деформируемому, см; hzGJCa,- радиальный прогиб шины, см.

При расчетах нагрузки на колесо наружной стороны Ок.и (нижний третий квадрант) принимается в момент опрокидывания на наклонной плоскости (см. рис. 74):

[со$ср(5/2-(-Я51п§)+Я51п(р].

Ок.и=-

Во втором квадранте приведено условие устойчивого движения по неравенству (77) с учетом угла наклона ад дорожного полотна 0...6°.

По данной номограмме, зная характеристики грунта проезжей части и обочины, можно определить (на рис. 76 построение показано тонкой линией со стрелкой) условие устойчивого движения по дороге данного состояния. Для оценки устойчивости таким способом должна быть проведена предварительная разведка маршрута движения с определением параметров грунта.

Особым случаем опрокидывания автомобилей с грузом может быть опрокидывание при воздействии ветровой нагрузки. Такой случай опрокидывания возможен для многоопорных транспортных средств, перевозящих грузы с большой парусностью. Опрокидывание под действием ветра можно рассматривать как действие динамических сил, переменных по времени. Ветровой поток не является постоянным, скорость порывов ветра может превосходить среднюю скорость в 1,5...2 раза и в этом случае возможно опрокидывание. В простейшем случае расчет устойчивости по условиям опрокидывания можно проводить, решая задачи равновесия с введением коэффициента динамичности Ка2.

38. ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ И ДИНАМИЧЕСКАЯ ПОПЕРЕЧНАЯ

УСТОЙЧИВОСТЬ

Физические процессы, сопровождающие опрокидывание от поперечных колебаний многоосных автомобилей, более сложные, чем те, которые рассмотрены выше. Очевидно, для установления закономерностей, управляющих опрокидыванием, необходимо подробно рассмотреть пространственную систему колебаний многоосного автомобиля на неровностях пути. При решении поставленной задачи используем подход, исходные предпосылки, упрощения расчетной схемы и частные допущения, принятые в гл. II при исследовании вертикальных и продольно-угловых колебаний многоосных автомобилей. Главное внимание сосредоточим на установлении влияния общих конструктивных решений на поперечную устойчивость по опрокидыванию, при поперечных колебаниях.

Принятая к исследованию расчетная схема поперечных колебаний изображена на рис. 77.

Согласно схеме дополнительные поперечные колебания будем рассматривать в двух обобщенных координатах F и у с учетом колебаний по координатам 2 и ф и двух вспомогательных координатах q я t,.

В дополнение к силам, действующим в системе подрессоривания, рассмотренным в подразд. 9,

появляется в контакте шин с дорогой боковая переменная сила Y, которую согласно деформационной теории будем определять из выражения

где Сб - коэффициент боковой жесткости, а Дв -боковая деформация шины, Дб/=Яу-г/ (рис. 77).

Из-за появления поперечных колебаний по координатам у и у подлежат уточнению выражения перемещений в подвеске:

Д =г - + by -{-I,г, ipi=z-t, + by+li.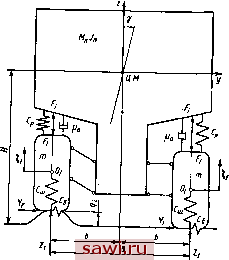

Рис. 77. Расчетная схема колебаний

поперечных

Поперечные колебания могут быть описаны следующей дополнительной системой дифференциальных уравнений (обозначения согласно рис. 77 и 15):

Му-\-2пСбУ = 2пСбНу;

J,y+2nv.,b(2C,b-\-2nC,W-M,gH) у==2пС,Ну+

liaC;+(Ср+Сц.) сi=Сц.; - Ср (г+*y+tff) +

+ ia(- + Y + ?).

Поделим все члены уравнений соответственно на М , Jx и nii и произведем преобразования по методике, изложенной в подразд. 9, в результате получим дополнительную систему дифференциальных уравнений поперечных колебаний, аналогичную по построению и значениям входящих коэффициентов дифференциальным уравнениям вертикальных и продольно-угловых колебаний, приведенным в гл. II:

y+2*tY+< ty=Q7; ii+2ki,C+4b=Ql.

При отсутствии амортизатора в системе поперечных колебаний по оси у парциальный коэффициент затухания колебаний системы Ку=0.

Для исследования полученной системы дифференциальных уравнений принципиально важным вопросом является выбор расчетных неровностей дороги. Учитывая характер поставленной задачи и опыт эксплуатации многоосных автомобилей, в качестве дорожных возмущений примем гармонические неровности, по которым автомобиль движется колесами одной стороны. В этом случае можно получить ярко выраженные поперечные колебания автомобиля максимальной интенсивности в резонансном режиме движения. В практике опрокидывание под воздействием поперечных колебаний происходит только при резонансных поперечных колебаниях. Если неровности микропрофиля дороги имеют случайный характер, потеря поперечной устойчивости в результате опрокидывания вряд ли возможна. Кроме того, детерминированное возмущение под воздействием гармонических неровностей микропрофиля опорной поверхности позволяет сравнительно точно оценить влияние общих и отдельных частных конструктивных решений автомобиля на устойчивость движения.

Для решения полученной системы дифференциальных уравнений можно использовать как ЭВМ, так и операторный метод Лапласа или матричный способ.

При сравнительных расчетах был принят гипотетический ряд многоосных автомобилей, имеющих число осей от 2 до 12 и тележечную схему расположения осей по базе. Нагрузка на колесо принималась постоянной для всех автомобилей (?к=59 кН. Отношение неподрессоренных масс к общей массе было принято равным 0,1. Жесткостные параметры подвески выбирались из условия обеспечения хороших показателей плавности хода автомобилей и соответствовали значениям Ср= (4...б) 10 Н/м; Сш= = (1...1,2) Н/м; Сб= (0,4...0,7) Сщ. Сопротивление амортизаторов определялось по зависимости:

0j, рад/с 25

!х, = ф,1/ 2Ср(Ж г),

где г)г - парциальный коэффициент апериодичности вертикальных колебаний (по статистическим данным г5г=0,2 ... 0,3).

Ширина колеи, высота центра масс принимались по среднестатистическим данным выполненных конструкций. Из условий ограничений транспортирования железнодорожным транспортом В<2,7 м. Моменты инерции определялись по эмпирическим зависимостям.

Ниже проведем анализ некоторых сравнительных расчетов и результатов эксперимента.

Изменения частот собственных колебаний, коэффициентов затухания и возмущающих функций поперечных-колебаний зависят от числа осей автомобиля. Расчеты показали (рис. 78), что колебания по обобщенной координате у так же. как н по координатам 2 и ф, являются низкочастотными. С увеличением числа осей частота колебаний Ют уменьшается и для автомобилей с любым числом осей она ниже частоты колебаний по координатам z, ф. Частота поперечных колебаний щ значительно (в несколько раз) выше частот других колебаний и приближается к частоте колебаний неподрессоренных масс. От числа осей частота колебаний по обобщенной координате у практически не зависит, так же как частота вертикальных колебаний. Следовательно, ре- р изменения собст-зонансные колебания по обоб- веяных частот колебаний в завн-щенным координатам у, ф и 2 снмости от числа осей