Глава VII

КОНСТРУКЦИЯ АВТОМОБИЛЯ и ПРОХОДИМОСТЬ

Как было показано, основной причиной создания многоосных автомобилей является стремление понизить нагрузку на ось и тем самым повысить вездеходность колесной машины, т. е. способность двигаться в тяжелых дорожных условиях. Важное значение имеет проходимость автомобиля, под которой понимают его способность двигаться по плохим дорогам и вне дорог с преодолением естественных и искусственных препятствий без вспомогательных средств.

Проходимость, как известно, особенно важна для полноприводных многоосных автомобилей, которые предназначены для работы на плохих дорогах, на распаханных полях в сельском хозяйстве и в условиях бездорожья. Важное значение проходимость имеет и для многоосных крановых шасси, работающих на строительных площадках и подъездных путях к строительным объектам.

Понятие вездеходности кроме проходимости включает свойство проезжаемости, способность автомобиля двигаться по дорогам с различными покрытиями и инженерными сооружениями без их разрушения (по мостам, дамбам, трубам и т. п.). Это качество особенно важно для многоопорных автомобилей, предназначенных для перевозки сверхтяжелых грузов.

В последние годы были разработаны новые типы автомобилей, которые обладают высокими показателями проходимости. Однако до сих пор отсутствуют аналитические методы оценки проходимости наземных транспортных средств в целом и нет единых обобщенных показателей, определяемых экспериментально. Такое положение объясняется чрезвычайной сложностью и многообразием явлений взаимодействия автомобилей с внешней средой, определяющих проходимость. Кроме того, очень много факторов, зависящих как от автомобиля и водителя, так и от внешней среды, влияют на возможность движения в сложных дорожных и климатических условиях. В настоящее время проходимость автомобилей оценивают сравнительным методом: сравнивают отдельные характеристики и конструктивные особенности автомобилей, а также поведение их при испытаниях в сложных дорожных условиях как при одиночных, так и при специальных групповых заездах.

Проведем анализ связей общих конструктивных решений с некоторыми показателями, характеризующими проходимость

автомобилей. При этом остановимся лишь на отдельных особенностях, обусловленных применением большого числа осей и их размещением по базе.

41. ВЗАИМОДЕЙСТВИЕ МНОГООСНОГО ДВИЖИТЕЛЯ С ДЕФОРМИРУЕМЫМ ГРУНТОМ

Для установления закономерностей влияния многоосного движителя на параметры опорной проходимости прежде всего необходимо проанализировать взаимодействие с грунтом одиночного колеса. Из всего многообразия известных грунтовых опорных поверхностей многоосные автомобили проявляют свои характерные особенности на деформируемых, уплотняемых грунтах определенной группы. К таким грунтам относятся связные грунты в пластичном и рыхлом состояниях с низкой несущей способностью (глины, суглинки, супеси в твердом, пластичном и текучем состояниях, пески, галечники, крупнообломочные породы). К грунтам этого типа могут быть отнесены грунтовые дороги при их увлажнении. Зимой к деформируемым опорным поверхностям можно отнести зимние дороги и местность со снежным покровом. Таким образом, деформируемые грунты являются наиболее представительной опорной поверхностью, по которой осуществляется движение многоосных автомобилей. Все прочие грунтовые условия для колесных машин не являются характерными.

В технической литературе известно несколько расчетных схем и несколько математических описаний качения колеса по деформируемому грунту. Это работы известных советских специалистов Я. С. Агейкина, В. Ф. Бобкова, Г. Б. Безбородовой, Н. Ф. Кошарного, И. С. Полякова и др. За рубежом этим вопросом занимались М. Г. Беккер, Дж. Вонг и др. Для достижения поставленных в данной книге целей наиболее подходит теория качения колеса по деформируемому грунту, разработанная Ю. В. Пирковским и расширенная и дополненная М. П. Чистовым [14, 19]. Особенность этой теории состоит в базировании ее на широких и разносторонних экспериментах, поставленных как с одиночным колесом, так и с многоосным движителем на раз-, личных представительных грунтах. Эксперимент дал большой статистический материал, который широко использован при построении теории качения колеса. Кроме того, эта теория описывает качение жесткого и деформируемого колеса с единых исходных позиций.

В основу разработанной теории положена гипотеза, подтвержденная экспериментально, о том, что сила, касательная к траектории движения элементарного участка колеса, изменяется пропорционально длине ее перемещения в грунте и что упругость и липкость грунта малы и ими можно пренебречь.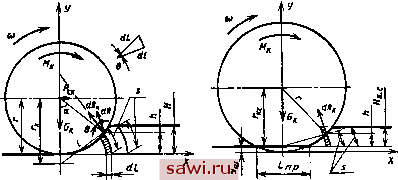

Рис. 85. Расчетная схема качения по мягкому грунту колеса: а - жесткого; б - дефорияруеиого

В соответствии с расчетной схемой (рис. 85, а) по аналогии с закономерностями сопротивления грунта вдавливанию касательная элементарная сила может быть представлена зависимостью:

dR-=c,B{S-srdl, (78)

где Сг - удельное сопротивление грунта вдавливанию штампа при погружении элементарной площадки на 1 см; д. - безразмерный степенной параметр, характеризующий закон изменения сопротивления по глубине вдавливания (в механике грунтов параметры грунта Сг и д, связаны зависимостью q=Crh*. характеризующей удельное сопротивление вдавливанию штампа q на глубину h); Sk--ширина беговой дорожки колеса; 5 - полный путь перемещения точки на ободе колеса от входа в грунт до выхода колеса из грунта по кривой, описываемой циклоидой; S -текущее значение пути; d/ -длина элементарной площадки, перпендикулярной к элементарной касательной силе.

По результатам обработки экспериментальных данных длина циклоиды может быть выражена степенной функцией через радиус жесткого колеса г, радиус качения Гк и глубину образуемой колеи Як:

S=\Oг(-)Hl,

(79)

Где показатели степени выражаются регрессионными зависимостями:

k=0,204 {rjrf - 0,408 (г,/г) -f 0,219; л=0.76(г,/г)г-0,35 (rjD-f 0.6.

На основании приведенных зависимостей можно получить выражение работы деформации грунта за один оборот жесткого колеса:

\<Уг(-)c,B,гJr I dL{н:hTdh, (81)

где dL - длина элементарной площадки на ободе колеса; h - текущее значение глубины колеи.

11римем в качестве исходной позиции качение колеса в свободном режиме, когда горизонтальная сила иа оси колеса Рт.к= = 0 и крутящий момент на колесе

aMdP,j=dO,x,

где Gk - сила тяжести, приходящаяся на колесо; х -плечо.

Кроме того, для жесткого колеса Гк=г, kO и n l. Тогда из выражения (80) можно получить основополагающие зависимости, характеризующие взаимодействие колеса с грунтом:

сопротивление качения колеса

(2i4-lq )2+i (1 2/3;х+ 1/5(х2)

глубина образуемой колеи

2(и.+ 1)

\1/(Ч-0,5)

(82)

(83)

\сМгг(2~ 13(х/15+ 1/5,а2) ;

Для режимов качения, отличных от свободного, зависимости должны учитывать удельную силу тяги колеса кг.к = Ргж/Ок, отношение радиусов качения и показатели степени k и п. Тогда

/г.к=/г.к.с+т.к(к.с/к-1); (84)

Ок [/г.к.с + Лг.к-к.с/-к - 1)]

,0*!;.М1-п)сВ[1 + 1)] +;х(;х 1)/2(2/г + 1

(85)

Полученных выше зависимостей вполне достаточно для анализа взаимодействия жесткого колеса с грунтом по всем параметрам с требующейся для практики достоверностью.

Уравнение мощности сопротивления качению жесткого колеса в свободном режиме

о 1 \

(20)2+1 1 з/5х-ь-2

где шк - угловая скорость колеса.

211+2

Мощность сопротивления качению в ведущем, тормозном и ведомом режимах качения колеса определяется зависимостью

Представляющей собой сумму потерь на качение в свободном режиме качения колеса и потерь на его проскальзывание.

Сопоставление расчетных данных с экспериментальными, показанное на рис. 86, дает их удовлетворительное совпадение и подтверждает возможность практического использования предложенных зависимостей.

Из графика видна зависимость сопротивления качению от режима работы колеса. Мощность сопротивления качению возрастает в параболической зависимости от буксования и от юза колеса. Это связано главным образом с затратой энергии на образование колеи в грунте. Оптимальным режимом является режим свободного (без проскальзывания) качения, когда 6 = 0.

Из графика также видно влияние на сопротивление качению Nf2 и на глубину колеи Яг повторного прохода колеса по одному следу на деформируемом уплотняемом грунте. Сопротивление качению и прирост глубины колеи уменьшились по сравнению с их значением при первом проходе колеса вследствие изменения характеристик грунта.

Экспериментально доказано, что при расчете взаимодействия деформируемого колеса по зависимостям для жесткого колеса велика погрешность, причем она тем больше, чем меньше рабочее давление в шине. Учет поправок на деформацию шины при

введении эквивалентного радиуса жесткого колеса точность расчетов не повышает, особенно для

0,08

-Ю О 10 20 30 WS,°/o

давлением.

М. П. Чистовым предложена уточненная расчетная схема качения деформируемого колеса (см. рис. 85, б) и дано ее математическое описание [19]. При разработке уточненных зависимостей, основываясь на широком

Рис. 86. Изменение мощности и глубины колеи в зависимости от коэффициента буксования и повторного прохода колеса по деформируемому грунту (по данным Ю. В. Пирковского):

2 - глубина колеи соответственно первого и второго прохода колеса; 3, 4 - мощность сопротивления качению;--экспериментальные: ----расчетные

экспериментальном материале, был принят ряд допущений и упрощений расчетной схемы.

Принято, что опора деформируемого колеса на деформируемом грунте имеет сложную геометрическую форму, состоящую из плоской части под центром колеса длиной Lnp и из цилиндрической части с радиусом г впереди колеса. Расстояние плоской части от поверхности грунта равно глубине образующейся колеи Як.с. Рассматривается вначале свободный режим качения колеса, при котором принимается Гк.с = г-уш- Среднее удельное давление на грунт в плоской части соответствует q=Cr\S\>. Удельное давление в цилиндрической части (7=15-s\. Принимается, что ширина отпечатка в контакте при изменении давления в шине не изменяется. На основании принятых допущений и расчетной схемы

dQ,dRUx + c,BSdL.

Первое слагаемое выражает элементарную нагрузку в цилиндрической части, а второе в плоской части опоры колеса на грунт.

После интегрирования приведенного уравнения 0 = A,A2AЛ{И,.,+yJ°-y .Ч + A,L /n., (86) где коэффициенты Ai=c,B; 10*гИ1- );

\ л+0,5 2(2л-1-0,5); VT?

Приведенная длина плоской части находится по эмпирической зависимости

L,p=FJB,=2Vyu.{2r-yJ-0,\57{r~yJ-0,2\5B,. (87)

Прогиб шины определяется по ее жесткости Сш и нагрузке на колесо

yOjC.

Удельная работа деформирования грунта численно равна коэффициенту сопротивления качению от деформации грунта, может быть представлена в уточненном виде с учетом радиального прогиба шины выражением

(88)

Л4=1

л-fl 2(2лЧ-1)

Для решения уравнения (86) необходимо предварительно определить глубину колеи по выражению (85), которая опре-