Эга особенность нелинейных муфт является особенно полезной, когда нагрузка в машине растет пропорционально квадрату скорости. Использование в этом случае линейной муфты приводит к большо.чу углу попорота полумуфт на высоких скоростях или излишней жесткости на низких. При зависимости момента сопротивления от скорости вращения вала и работе машины в дорезонансном режиме отношение рабочей скорости вращения к критической в агрегате с линейной муфтой резко увеличивается с ростом нагрузки. Запас устойчивости падает. В нелинейной муфте с увеличением нагрузки растет жесткость и с той же тенденцией меняется собственная частота системы. Критическая частота вращения

агрегата с ростом нагрузки существенно растет.

Нелинейные муфты имеют преимущество при разгоне машины и особенно во время выбега при ее остановке. При отсутствии нагрузки, что часто имеет MecTip при выбеге, критическая частота вращения агрегата с нелинейной муфтой лежит близко к нулю. В этой области вряд ли возможны большие колебания, так как при их возникновении соответственно изменяется критическая частота врагцення. В агрегате с линейной .муфтой прохождение области резонанса при выбеге занимает гораздо больше времени и колебания могут достичь значительной величины. Если после отключения двигателя нагрузка не сбрасывается, резонансные колебания в агрегате с нелинейной муфтой будут меньше колебаний в агрегате с линейной муфтой (рис. HI.2). На рисунке 2 - отЕЮшение рабочей частоты вращения к критической.

Жесткость упругих муфт зависит от многих факторов, в том числе и от качества изготовления, и часто задается в виде графиков. При работе упругих муфт всегда имеют место потери энергии на трение (внутреннее и внешнее), сопровождающее деформацию ее упругих элементов и их перемещение относительно других элементов.

Отношение энергии, потерянной за один цикл нагружения муфты, к работе сил упругости за четверть периода называется коэффициентом демпфирования гз.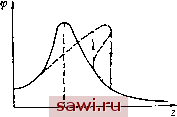

Рис. П1.2. Колебания в агрегате с линейной муфтой

2я/(0

(И1.1)

Здесь f - коэффициент, позволяющий при расчетах заменить действие демпфирующего момента УИд действием эквивалентного демпфирующего момента, величина которого линейно зависит от скорости дефор.мации (УИд -/ф); ы - частота колебаний. В каталогах обычно приводятся значения С и ij). Поскольку в дифференциальные уравнения агрегата входит величина f, то в случае решения уравнений на моделирующей машине значения f находятся из формулы (П1.1). При этом величину со реко.меидуется брать равной собственной частоте системы [68].

2. РАБОТА ЛИНЕЙНОЙ МУФТЫ ПРИ ПЕРИОДИЧЕСКОЙ НАГРУЗКЕ

В качестве динамической модели машинного агрегата рассмотрим двух-массовую систему. При этом предполагается, что податливость всех деталей машины, передающих крутящий момент, пренебрежимо мала по сравнению с податливостью муфты. Если момент двигателя не зависит от скорости и равен постоянной составля;ощей нагрузки, дифференциальное уравнение движения можно привести к виду

Ф + .

(П1.2)

где . ф = ф1 - Фа;

ff--приведенный момент инерции; ф - угол

поворота вала двигателя; Фа - угол поворота входного вала машины; и - моменты инерции двигателя и машины, приведенные к валу муфты; М (t) - нагрузка со стороны машины.

При нулевых начальных условиях ( = 0; Ф = 0; Ф = 0) общее решение дифференциального уравнения (П1.2) имеет вид

М (X) sink (t - x) dT,

J.k J

где ft =

собственная частота.

пр г J пр

Если известна зависимость ф (t),m выражение момента в упругой муфте М в предположении линейной зависимости демпфирующего момента от скорости деформации находят по формуле

М= C(f + fq).

В частном, но важном для практики случае гармонического возмущения М (t) = Ml sin tot стационарная часть решения равна

Л1 = *д-Т-4Ь-1 sin ((0/-Р). (И1.3)

l i~ 2

Здесь кц - коэффициент динамичности, равный

(III.4)

Р - сдвиг фаз.

При sin (<i)t - Р) = 1 момент в муфте достигает максимального значения.

Величина коэффициента динамичности, определяющая нагрузку на муфту, зависит от величины коэффициента демпфирования гз и отношения шк. Характер этой зависи.мости показан на рис. П1.3.

Если возмущающий момент приложен со стороны массы Уц то вместо формулы (П1.3) имеем

Л1 = д-7-тЧ-sin (©< -р). (П1.5)

1 -г г

Максимальный момент наступает при резонансе (о = k. В этом случае

max - *2 + 1

При <£ 12йд всегда больше единицы, а при V2 - всегда меньше

единицы. При работе агрегата в зонах, далеких от резонанса, демпфирование можно не учитывать. При работе агрегата в зарезонансной зоне упругая муфта делает работу ведо.мых частей более плавной. Однако, учитывая прохождение зоны резонанса при разгоне и выбеге, необходимо выбирать муфту со значительной демпфирующей способностью или ставить нелинейную муфту с жесткой хар актер истикой.

г Зависимость момента двигателя от скорости учитывают при составлении уравнения движения. Так, коэффициент динамичности с учетом линейной

зависимости момента электродвигателя от скорости при пренебрежении членами второго порядка малости будет равен [58]

2-(l+t) + Yf

(III.6)

У и

где ц = у = -jY ~ изменение крутящего момента двигателя при единичном изменении скорости вращения ротора.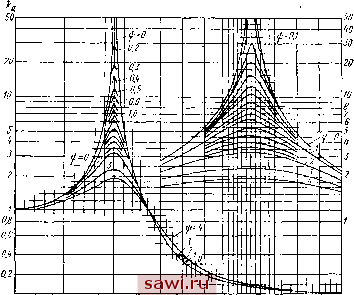

О 0,5 1 f,6 г J if >/>< Рис. III.3. Кривые зависимости от и ш/А

Учет электромагнитных процессов в электродвигателе при нахождении Ад рассмотрен в [59]. Действие произвольного возмущающего момента М {t) можно исследовать двумя способами: способом Дуффинга или представляя функцию М (t) рядом Фурье, коэффициенты которого находятся по известньш формулам [68].

Пример 1. Машинный агрегат состоит из двигателя постоянного тока П-62 н исполнительного устройства, соединенных упругой муфтой МУВП (Уд = 1,65 кгсХ Хсм-с; С = 50 ООО кГс см/рад; ф = 0,63). Отношение моментов инерции исполнительного устройства и двигателя равно 2. Оценим влияние двигателя на величину максимального момента при резонансе.

Приведенный момент инерции равен

1,65.2-1,65 2.1,65 -f 1,65

Собственная частота системы

50-103 1.1

= 1,1 кгс-см-с.

= 212 с-1.

На основе каталожных данных двигателя и величины % находим у = 0,17. Величина коэффициента динамичности при резонансе по формуле (III.6)

0,63 2-3,14

= 1,6.

(1-f 2)+ 0,17-2

Величина коэффициента динамичности без учета влияния двигателя (т = 0)

0,63 4-3,14

0,63 2-3,14

= 3,33.

(1+2)

Таким образом, участие двигателя в демпфировании колебаний понизило пик нагрузки более чем в два раза.

Пример 2. Одноцилиндровый четырехтактный двигатель с номинальной мощностью Ло = 22 л. с. и номинальной частотой вращения Пц - 1500 об/мин приводит в движение генератор, присоединенный к нему с помощью линейной муфты (С = ЗХ X 10* кгс. см/рад; i) = 0,5). Моменты инерции (приведенные к оси муфты): У, = 105 кгсХ Хсм-с; Уз =! 40 кгс-см-с. Момент сопротивления предполагается постоянным. Определим момент на ведомых частях агрегата.

Номинальный крутящий момент равен

Мр = 71 620

--= 71 620

1500

1050 кгс-см.

Угловая скорость

03 =

ЯП 3,14-1050

= по с-1.

Приведенный момент инерции

105-40

Р 105 + 40

= 28,9 кгс-см-с.

Собственная частота

1 с-1.

Возмущающий момент двигателя может быть разложен в ряд Фурье, при этом порядок гармонических составляющих определяется по формуле

а= 1, 2, 3, . . .,

где (Одози - угловая скорость возмущающего момента; (О - угловая скорость агрегата.

Для одноцилиндрового четырехтактного двигателя Ивозм ~ Рабочий

ход иа два оборота). Величина i может принимать значения 0,6; 1; 1,5 .. .

Частота воз.мущающего момента равна io). Величина гармонического возмущающего момента может быть определена на основании формулы

Mi = riMp.

Величина т] определяется исходными данными о двигателе.

На основании фор.мул III.4 и III.5 находим величину коэффициента динамичности от возмущающего момента порядка i с учетом соотношения масс двигателя и генератора. Например, при i = 1,5 имеем

0,52

4-3,142

1,52.1102 \2 0,52 105 + 40

(] 1,5-1102 \2

V 32,12 ;

= 0,00546

32,12 J 4-3,142 (мы определяем максимальный момент при sjn {at Э) = U-

£

- CO

vq О

s я о

я s s

§ S

i §

s is:

S а.

sis

я Я о-

Возмущающий момент на ведомой части АГ -Л1,.Ад -г-гт = крПл / 1050-2,9-0,00546 = 17.

Все вычисления по пяти гармоникам представлены в табл. 1П.1.

Для сравнения в этой же таблице приведены величины моментов М, вычисленные для случая соедннеиия жесткой муфтой. Результаты показывают, что применение упругой муфты позволило значительно уменьшить величину момента, воздействуюи1его на генератор при С = 0,5; 1. При i > 1 влияние возмущающего момента сведено на нет. Применение жесткой муфты и при i > I дает большие значения момента М.

3. РАБОТА НЕЛИНЕЙНОЙ МУФТЫ ПРИ ПЕРИОДИЧЕСКОЙ НАГРУЗКЕ

Наличие нелинейной муфты создает особенности в работе агрегата при динамических режимах, в частности, затягивание резонанса в область высоких частот, возможность возникновения колебаний с частотой в целое число раз меньшей, чем частота возбуждаюш,его .мо.мента. Уравнение движения системы с ]1елинейной муфтой имеет точное решение лишь в отдельных случаях. При расчетах таких систем большое значение имеет зависимость частоты k от амплитуды при свободных колебаниях. Эта зависимость в графической форме носит название скелетной кривой. Виды скелетных кривых для некоторых нелинейных зависимостей вместе с формулами, связывающими частоту с амплитудой, даны в табл. III.2. Для построения скелетных кривых обычно пользуются приближенными способами [15]. При этом заранее предполагаются (например, на основании эксперимента) существование дифференциального уравнения движения и форма его периодического решения. При гармонической линеаризации считают, что режим колебаний близок к гармоническому. Решение в общем случае получаем в виде ф = фо + -]- Ф cos (at + а). Частота свободных колебаний (скелетная кривая) может быть найдена из приближенных формул:

* аГ (Фо4-Фсо8<))1[;--=0; (III.7)

М [фр (Ф) -f Ф сов il)] cos ф d-ф.

(III.8)

Здесь г1) - а>{; ф - смещение середины размаха колебаний относительно положения равновесия.

Если с помощью (III-7) выразить фо через Ф и подставить в (III.8), то получится зависимость k (Ф) - скелетная кривая.

Характеристика некоторых типов шинных муфт может быть апроксимирована двучленом М (ф) = С1Ф-f Саф . Подставляя М (ф) в уравнение (III.7) и учитывая, что ф = фо + Ф (cos ш), имеем

[Ci (Ф + Ф cos ф) -f Q (Ф -f Ф cos ф)3] йф =

2л J

= 0.

Из уравнения (III.8) имеем 2я

[Ci (Фо + Ф cos ф) -I- Сг (Фо + Ф cos ф)3] cos ф йф =

пр .