Виды скелетных кривых

Характеристика восстапавлипающего момента

Частота свободных колебаний

Связь амплитуды свободных колебани!! с их частотой

Л1 = Сф

М = С(ф + ф ) при ф < - фо; М = 0 при - Фоф5£Фо; М = С (ф - ф ) при ф > ф

-JPo

Муфта с зазором

д(а-1)

где а -=

> 1

Муфта с натягом

где а =

я -2 arcsin а Фо

Сф-гФо

< 1

М = аф

= ]/ф 2 V( )

V2 (п+\)

Учитывая первое уравнение, фо = 0. Тогда уравнение скелетной кривой будет

При о скелетной кривой будет ветвь гиперболы (рис. III.4).

Максимальная амплитуда имеет место вблизи точки пересечения скелетной кривой и кривой резонансных амплитуд Фщах

Ml (со) пр

Например, если Mi= const, то кривая Фщах (< ) - гипербола. С жесткой скелетной кривой она может пересекаться один раз, с мягкой - два раза или может вообще не иметь точек пересечения.

Если максимальная амплитуда не превосходит допустимой, то нет необходимости строить всю амплитудно-частотную характеристику. В противном случае амплитудно-частотная характеристика может быть построена с помощью формулы [33]:

i) (III.9)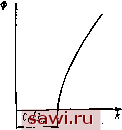

пр V[k (Ф) - а>2]2 -г- 4n2(u2

Рис. 14.4. Скелетная кривая

где п - -

В (III.9) (Ф) определяется уравнением (III.8). Совместное решение урав-нс}1ий (III.8) и (III.9) удобно производить графическим путем. Для этого по формуле (III.9) строится график зависимости Ф (k), причем k рассматривается как независимая переменная. Величина m предполагается постоянной. На этот же график наносится скелетная кривая k (Ф). Точки пересечения кривых определяют решение уравнения (III.9) при выбранно.м значении со (рис. III.5, а).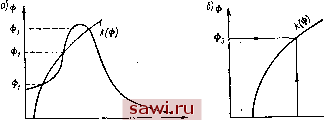

к к/З ш

Рис. III.5. График зависимости Ф (k)

Уравнение может иметь несколько решений (иа рис. III.5, а три решения), соответствующих нескольким колебательным рел<имам. Величина амплитуды, устанавливающаяся в действительности, зависит от начальных условий. Изменяя значение ш, можно найти зависимость Ф (со) - амплитудно-частотную характеристику системы. Величина амплитуды при субгармоническом резонансе (т. е. при частотах kip; р = 1, 2, 3 . . .) и гармоническом возбуждающем моменте может быть приближенно оценена на основании скелетной кривой, как это показано на рис. 111.5,6 для случая р = 3. Вопрос об условии существования

* Поляков и др. 65

субгармонического резонанса при линейном трении может быть решен на основе исследования неравенства

<

Р I Фр 1

(ОФ?

(ШЛО)

Здесь Ф - амплитуда при основном резонансе (р = 1); Фр - амплитуда при субгармоническом резонансе порядка р. Субгармонический резонанс невозможен, если не удовлетворяется неравенство (III.10).

В муфтах с неметаллическим упругим элементом жесткость при медленном нагружении и разгружении (статическая жесткость) значительно отличается от жесткости, проявляемой в динамических режимах (динамической жесткости). Это обстоятельство должно учитываться при расчетах. Динамическая жесткость упругих муфт находится при испытании последних в динамических режимах [55].

Методы расчета систем с нелинейными упругими муфтами изложены, например, в [11, 15].

4. РАБОТА УПРУГОЙ МУФТЫ ПРИ УДАРНЫХ НАГРУЗКАХ

Закон изменения момента сопротивления при ударе может иметь различный характер. Приведенные ниже формулы получены в предположении изменения момента при ударе согласно рис. III.6 и малости демпфирующей способности муфты. На рисунке Л1о - начальная нагрузка; My - величина наброса нагрузки; X- время между началом нарастания нагрузки и моментом возвращения к стационарному состоянию (время удара).

Максимальная деформация фтах при ударе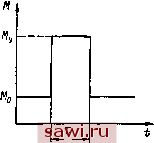

фгаах = <Ро

S2-M

Рис. II 1.6. Изменение при ударе

момента

где Фо - деформация, соответствующая Мо-Деформация фщах достигается, если имеет

место соотношение ~ При этом максимальный момент Мщах, передаваемый муфтой, равен

МшахМо-f 2., , М

J, + J,

При абсолютной жесткой муфте Мщах = Мо + My. Таким образом, упругая муфта смягчает длительный удар в том случае, если J Ji- Это положение справедливо при любой конечной жесткости муфты- При коротком ударе, когда . я

Тч-, ф не успевает принять максимального значения, нарастая в течение всего удара. Максимальный момент при коротком ударе

: = Мо -f 2

Амортизация короткого удара происходит в том случае, если

Ji + J,

< 1.

т. е. тем больше, чем мягче муфта и больше Упр-66

Зависимость деформации ф от времени с учетом демпфирования может быть найдена по формуле [57]

1 - . sin {k\r 1 pa + а)

Ф =--J-

где Р =

С Л + а а = arccos р.

Если время действия удара мало, можно использовать приближенную формулу определения момента в муфте

Зависимость момента двигателя от скорости влияет на характер переходного процесса агрегата с упругой муфтой. Построение переходного процесса в машинном агрегате с электродвигателем и упругой муфтой рассмотрено в [13]-

А, МУФТЫ С МЕТАЛЛИЧЕСКИМИ УПРУГИМИ ЭЛЕМЕНТАМИ

Эти муфты отличаются высокой несущей способностью и возможностью работы в широком температурном интервале, однако они сложны по конструкции, дороги и обычно требуют постоянного кбнтроля при эксплуатации.

5. МУФТЫ С ПАКЕТАМИ ПЛАСТИНЧАТЫХ ПРУЖИН

Муфта с радиальньши пакетами пружин показана на рис. П1.7. Полумуфты 1 и 5 соединяются пакетами пружин (рессор) S, работающих на изгиб при действии крутящего мо.мента. С полумуфтой 5 пакеты пружин соединяются через кольцо 3, имеющее продольные пазы, с помощью болтов Внутренние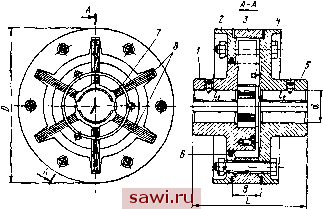

Рис- III.7. Муфта с радиальными пакетами пружин

концы пакетов пружин входят в радиальные пазы полумуфты 1. Пакеты пружин фиксируются на полумуфте 1 с помощью кольца 7 и трех винтов. Крышка 2 с уплотнением 6 закрывает внутреннюю полость муфты, заполненную густой смазкой.

Основные раз.меры и параметры этих муфт даны в табл. III.3. Муфта имеет линейную характеристику до тех пор, пока касательная к упругой линии

Таблица III.3 Размеры (в мм) и параметры муфты (рис. III.7)

деформированной пружины не совпадет с линией скоса паза (рис. III.8); при дальнейшей деформации пружины характеристика муфты нелинейна.

Без учета влияния сил трения между пластинами полумуфты при действии крутящего момента /Ир повернутся на угол (pjj (рис. III.8)

гп г/л:+ (/-. ) Фдс -

R + X

где Ух = --прогиб пакета пружин; J - п --момент инерции поперечного сечения пакета пружин; & и Л - соответственно ширина и толщина од1Гой пластины пакета; п - число пластин в пакете; Е - модуль упругости 1-го рода;

- окружная сила, действующая на пакет на плече х; т -

т (R -г X)

число пакетов; а-профильный угол паза; и / - см. на рис. III.8.

На линейном участке характеристики зависи.мость угла поворота полумуфт ф1 от величины крутящего момента М без учета влияния сил трения определяется выражением

Ml 2mEJ (R + I)

Максимальные напряжения изгиба в пластинах пружин будут наблюдаться при X - а (рис. III.8), определяются они по формуле

где = --г--окружная сила, действующая на пакет; W = n-p-

tn [R -р fl) о

момент сопротивления поперечного сечения пластин; М2 = Лтах - крутящий

момент на муфте при х = а.

Число пластин в каждо.м пакете находят из выражения

m{R + a)Wt[o] где [а]й - допускаемое напряжение изгиба для материала пластин; Wx = 68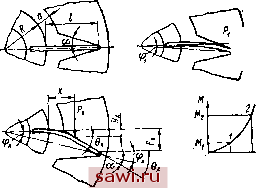

Рис. III.8. Схема работы упругой пружины переменной жесткости

ff-5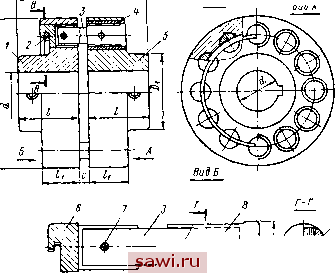

-4 \

Рис. И 1.9. Муфта с пакетами плоских пружин, расположенных параллельно оси вала, фирмы Waldron