минимальная толщина смазочного слоя /гщ становится больше - все неровности поверхностей скольжения перекрываются с избытком, непосредственный контакт цапфы и подшипника исклю- чается. В пределе при со со клиновый зазор превращаете в кольцевой с постоянной толщиной 0,55 = 0,b{D - d). Траектория, описываемая центром цапфы при непрерывном увеличении скорости вращения, близка к полуокружности с диаметром б = 0,5s. Положение центра цапфы при том или ином режиме работы вполне определяется величиной угла фа и эксцентрицитетом е.

Гидродинамические давления, развивающиеся в смазочном слое, распределяются неравномерно, максимальное удельное давление приходится на участок, смещенный от вертикальной оси в сторону вращения цапфы (фиг. 6). Характер эпюры давлений зависит от положения цапфы, места подвода смазки, границ смазочного слоя и некоторых других факторов. При положений центра цапфы на кривой О1О2О3О4 гидродинамические силы уравновешивают внешнюю нагрузку, действующую на цапфу, и оказывают сопротивление вращению цапфы. Работа, затрачиваемая на преодоление сопротивления вязкой жидкости, переходит в тепловую энергию; тепло, выделяющееся в рабочей зоне подшипника, отводится не только через детали опоры во внешнюю среду, но и в значительной мере уносится смазывающей жидкостью. Расход смазки, т. е. количество ее, протекающее через зазор между цапфой и подшипником -в единицу времени, зависит от тех же факторов, которые обусловливают, гид-родина-.мические силы.

Таким образом, для достаточно точного расчета подшипника скольжения должна быть установлена взаимосвязь целого ряда различных параметров: конструктивных размеров опоры, зазора между трущимися деталя.ми, свойств смазывающей жидкости, нагрузки, скорости вращения, способов теплоотвода и т. д. Ответ на этот вопрос дает гидродинамическая теория омазки. С достаточной полнотой теоретические основы работы подшипников скольжения изложены в монографии М. В. Коровчинского [21]. Инженер, желающий изучить гидродина.мическую теорию смазки, найдет в этой монографии анализ основных исходных положений обоснование расчетных зависимостей, необходимых для проектирования подшипников, и ряд ценных сведений, касающихся развития гидродинамической теории смазки. Здесь мы ограничимся кратким изложением методики гидродинамического расчета подшипника, ставшей, в известной мере, классической.

§ 15. ОПРЕДЕЛЕНИЕ НЕСУЩЕЙ СИЛЫ СМАЗОЧНОГО СЛОЯ

На фиг. 7 показаны два элемента А и Б, разделенные слоем вязкой жидкости. При произвольном перемещении поверхности А относительно поверхности Б в слое жидкости возникнут давле-62

ия, для определения которых служит обобщенное уравнение Рейнольдса

(46)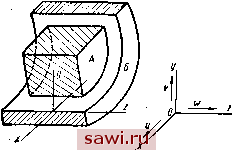

Здесь и, V, W-компоненты скорости движения .поверхности А относительно поверхности Б, направленные по осям Ох, Оу и Oz (фиг. 7); l - динамическая вязкость жидкости; р - плотность жидкости; h - толщина смазочного слоя в рассматриваемом сечении. ,

Уравнение (46) имеет силу для любого случая нестационарного движения вязкой сжимаемой жидкости, для которой величины ц и р не являются постоянными, но зависят от температуры, давления и координат рассматриваемой точки. Решение уравнения (46) в общем виде - задача чрезвычайно сложная, да и практическое использование такого решения было бы сопряжено с большими затруднениями. В применении к норма!льным цилиндрическим подшипникам уравнение может быть существенно упрощено при следующих условиях.

1. Если смазка осуществляется маслом или водой, т. е. несжимаемой жидкостью, то при t = const плотность ее р = const

и, следовательно, - - О; последний член правой части уравнения отпадает, а р можно исключить из обеих частей уравнения.

2. Если температура и давление жидкости изменяются по протяжению смазочного слоя в узких пределах и могут быть заменены с малой погрешностью средними значениями, то величину р. можно отнести к этим средним значениям и принять ее постоянной.

3. Для установившегося режима работы с постоянной скоростью вращения цапфы окружная скорость U в направлении оси Ох-также будет величиной постоянной: U = const.

4. Так как при этом центр цапфы не перемещается и эксцентрицитет e=const, то скорость V в направлении оси Оу равна нулю.

Фиг. 7. Элементы поверхностей цапфы и подшипника, разделенные смазочным слоем.

5. Так как скорость течения жидкости в направлении к торцам подшипника вдоль ,по оси Oz значительно меньше скорости в направлении вращения, то в первом приближении можно принять 1 = 0; это допущение равносильно предположению, что протяжение смазочного слоя в направлении оси подшипника неограниченно велико (подшипник бесконечной длины, / =со); исключение торцового истечения смазывающей жидкости приводит к плоскому потоку.

Перечисленные упрощения можно записать так:

р=: const;

[1 = const; ;7=: const; 1/=0;

(47)

С учетом этих условий уравнение Рейнольдса примет вид

(48)

В результате интегрирования уравнения (48) получим

h=Q]xUhC. . (49)

Постоянная интегрирования С определится из следующего условия: при некоторой толщине смазочного слоя h = h дав-

ление р достигает максимума; но при р-ртах имеем -j-P,

тогда из (49) найдем

После подстановки этого значения в-уравнение (49) получим

(50)

Для определения давления р в произвольном сечении под углом ф к линии центров (фиг. 8) удобнее пользоваться полярными координатами. Для перехода к ним произведем следующие замены:

dx = rdf; U=mr.