центра цапфы возрастает. Такое исходное положение цапфы в подшипнике называется неустойчивым, оно может явиться причиной опасных вибраций ротора. В машинах с быстровращаю-шимся хорошо отбалансированным ротором, например, в паровых и газовых турбинах, насосах, воздуходувках, сепараторах, центрифугах и пр., нередко наблюдаются такие вибрации, сопровождающиеся ударом цапфы о вкладыш, разрушением баббитового слоя и аварией машины. Поэтому исследование устойчивости цапфы в смазочном слое подшипника имеет важное практическое значение.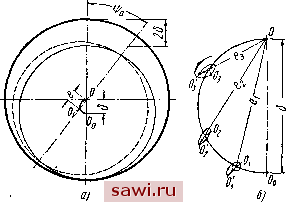

Фиг. 22. Устойчивое и неустойчивое положение цапфы

в подшипнике: а - перемещение враща1ои1.ейся цапфы в подшипнике; б - перемещение цевтра цапфы.

В общем случае цапфа, выведенная из положения равновесия, совершает следующие движения:

а) вращение вокруг своей оси с постоянной угловой скоростью;

б) колебания близ точки, лежащей на кривой подвижного равновесия, причем центр цапфы описывает некоторую траекторию. Эти колебания можно представить в, каждый данный мо-.мент как два взаимно-перпендикулярных перемещения:

радиальное, при котором центр цапфы дв.чжется по линии центров со скоростью U ;

тангенциальное, при котором центр цапфы движется со скоростью так, как если бы линия центров OOi была водилом,

вращающимся вокруг точки О с угловой скоростью Q = -~->

Каждому виду движения цапфы соответствует определенное течение вязкой жидкости в клиновом зазоре, а именно:

1) вращение цапфы вокруг своей неподвижной оси вызывает нвп,ре)рывное 1К(ругавое течение жидкости; при этом устанавливается определенный постоянный поток жидкости по нап-рав-

лению к торцам подшипника. Эти течения вязкой жидкости обусловливают величины несущей силы и сил сопротивления вращению;

2) радиальное перемещение цапфы заставляет вязкую жидкость течь в направлении стрелок аа - в обе стороны от плоскости, проходящей через ось подщипника и линию центров (фиг. 23), и в направлении стрелок бб - в обе стороны от плоскости, перпендикулярной оси подшипника;

3) тангенциальное перемещение цапфы вызывает дополнительный круговой поток жидкости.

Возникновение каждого дополнительного течения жидкости сопровождается соответствующим сопротивлением вязкой жид-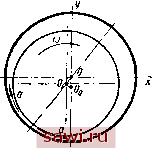

Фиг. 23. Течение смазки в нагруженной зоне прч радиальном ремещеини цапфы.

кости тому движению цапфы, которое вызвало данный поток. Эти силы сопротивления называются демпфирующими силами смазочного слоя; они зависят от вязкости жидкости, скорости цапфы в колебательном движении и от параметров подшипника.

Движение центра цапфы описывается дифференциальными уравнениями движения материальной точки в плоскости

(128)

Здесь Жмасса части ротора, отнесенная к центру цапфы; S, S - суммы проекций на оси координат сил, действующих на цапфу;

а) гидродинамических сил, соответствующих положению центра цапфы на кривой подвижного равновесия,--назовем х регулярными силами смазочного слоя;

б) демпфирующих сил смазочного слоя;

в) центробежных сил от неуравновешенных масс;

г) внешней нагрузки.

Решение дифференциальных уравнений движения центра цапфы в общем виде представляет собой весьма сложную задачу, в особенности при нагрузке, изменяющейся по величине и направлению (например в поршневых машинах); но при постоянной нагрузке и хорошо отбалансированном роторе, когда силы инерции неуравновешенных масс весьма малы и ими можно пренебречь, задача по определению условия устойчивости существенно упрощается.

Для турбин, электродвигателей и тому подобных машин, у которых нагрузка на опоры определяется весом ротора, дифференциальные уравнения (128) можно представить в виде:

M + R, + Q, = 0; + y + Qy = 0.

(129)

Здесь Rx, Ry - проекции на оси координат регулярных сил смазочного слоя; Qx Qii ~ проекции на те же оси демпфирующих сил; М - масса ротора, отнесенная к подшипнику. Регулярные силы смазочного слоя при известных параметрах подшипника и свойствах вязкой жидкости определяются координатами х, у точки, расположенной в силовом поле смазочного слоя. Компоненты Rx, Ry регулярных сил могут быть представлены в виде выражений

:=с:,+Ах.} <

Здесь множители С,-, D/ имеют размерность в кГ/л; их определяют обычно по методу, предложенному Гуммелем (52], с помощью силовых полей. (Однако способ этот практически неудобен и недостаточно точен. Проф. Е. М. Гутьяр [10] указал на весьма важные свойства отклоненной дуги подвижного равновесия.

Сущность метода определения регулярных сил на основе свойств отклоненной дуги заключается в следующем.

Цапфа может быть в равновесии только в том случае, ecл центр ее расположен на кривой подвижного равновесия OqOiO (фиг. 23). Для каждой точки этой кривой может быть найдена (при заданных параметрах подшипника и вязкой жидкости) равнодействующая гидродинамических (регулярных) сил. Под действием мгновенной возмущающей силы цапфа выходит из положения равновесия, причем центр ее может оказаться в некоторой точке с внутри круга, описанного )радиусом б = 0,5s (фиг. 24).