Отклоняя дугу подвижного равновесия вместе с жестко связанным с нею вектором несущей силы смазочного слоя Рс до соприкосновения с точкой с, определим величину регулярных сил Рс =Рс и угол а между направлением внешней нагрузки и вектором Рс- На основе этого свойства кривой подвижного равновесия, принятой за полуокружность диаметра б, были получены

следующие выражения для величин Си С2, -Dl, D2.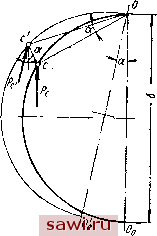

( VT-

Р [Л(й йФг

В рф2-Х- ах р \хи, аФр

5 /f dx

(131)

Фиг. 24. Определение регулярных сил смазочного слоя методом Е. М. Гутьяра с помощью отклоненной дуги подвижного равновесия.

полученной Кодниром

Здесь 8 - радиальный зазор в м;

]> - динамическая вязкость в кГсек/м\

р=-в кГ/м;

Фр - безразмерный коэффициент нагрузки подшипника. Для- дифференцирования Фр по х .можно воспользоваться зависимостью, [20]/ для подшипника конечной длины

Фр = -

1,02[1-(1-х)]

1 -f

/d I

[0,12-f 2,31 (1 -X)]

(132)

Демпфирующие силы смазочного слоя зависят от скорости перемещения центра цапфы U и могут быть выражены зависим мостью вида

Q = bU,

где е - коэффициент демпфирования, имеющий размерность в кГсек/м; U в м/сек.

При радиальном перемещении центра цапфы в направлении оси п (фиг. 25) для нормальной силы демпфирования получим выражение

Q = e f/ .

Соответственно для тангенциальной силы, обусловленной дополнительным течением жидкости в направлении вращения центра цапфы, получим

Проекции векторов этих сил на оси п и t составят тензор

QnnQnt QtnQtf

Соответствующий им тензор коэффициента демпфирования будет иметь вид

Для подшипника с углом охвата 180° (половинный подшипник) при ламинарном течении вязкой несжимаемой жидкости были получены следующие выражения для коэффициентов демпфирования 37]:

1 + 1

dY 1-х-

3. = -М.ф,;

(133)

Переход системы координат nt к системе ху (фиг. 25) осуществляется поворотом осей на угол -а, чему соответствует тензор

ух-уг

Матрица перехода будет

cos а -sin а sin а cos а

Замечая, что

sinar=x; Cos а = 1 -

перепишем матрицу так

V\-xJ

Следовательно,

= (1 - XJ) - 2х nt + X%t\

= у. = Х/1, - + (1 - 2х) 4t-xV\- Х

(135)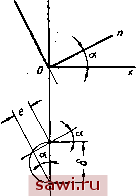

По приведенным коэффициентам демпфирования определим компоненты тензора сил демпфирования

Qy.Qyr (136)

Физический смысл этих компонентов таков.

Qxx представляет собой силу демпфирования, возникающую при .движении центра цапфы по оси х и действующую против движения

dx

(137)

Фиг. 25. Переход от си- Qyy ТО же. При движении ПО ОСИ у,

стемы ксюрдинат not к ау /юоч

(13о)

хоу.

О =е -уу уу dt

Qyx - сила демпфирования,7направленна5< по оси х при движении центра цапфы по оси у(

У dt

-(139)

Qxy - сила демпфирования, направленная по оси у при движении центра цапфы по оси х,

-ху dt

(140)

С учетом полученных выражений дифференциальные уравнения (122) примут вид

х dt dx

У dt

+ уу + С2У + Ох = 0.