ник с двумя клиньями; он может быть получен расточкой из двух центров или смещением верхней половины вкладыша относительно нижней. При положении центра цапфы в точке Oj основная зона давлений будет внизу - в нагруженной части подшипника, но и в верхней части возникают гидродинамические давления благодаря эксцентрицитету цапфы по отноше нию к верхней половине вкладыша В случае ненагруженного (например, вертикального) ротора центр цапфы расположится в середине между центрами вкладышей Og и 0 и обе эпюры давлений будут симметричны.

На фиг. 32 показан двухклиновыт ! симметричный подшипник для реверсивного вращения вала; он может быть получен расточкой разъемного вкла дыша с прокладкой в плоскости стыка (фиг. 32, а); после удаления прокладки собранный вкладыш будет иметь очертания, показанные на фиг. 32, б. Такие подшипники, образно называемые лимонными , часто применяются для паровых турбин. Несущая способность таких подшипников меньше, чем подшипника по фиг. 31, так как при любом направлении вращения дуга охвата в каждой половине вкладыша не превышает четверти окружности.

Фиг. 31. Подшипник с двумя масляными клиньями.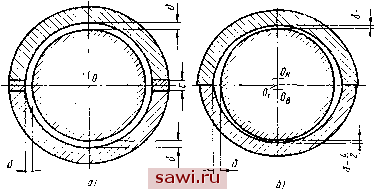

Фиг. 32. Схема лимонного подшипника:

а - вкладыш с прокладкой перед расточкой; б - собранный без прокладки вкладыш.

Положение цапфы в лимонном подшипнике характеризуется двумя эксцентрицитетами по отношению к каждой половине вкладыша. Благодаря этому возникают масляные клинья с обеих сторон, с соответствующими гидродинамическими давлениями 140

Возможные колебания центра цапфы ограничены областью О1О2О3О4 (фиг. 33). Рассматривая произвольную точку в этой области и применяя метод отклоненных дуг (фиг. 34), получим

S = - £in К + 2 sin &2 = 0;

2 K=-P+/=jCOS fti-FjCOSdz,

(174)

где Fi и р2 - гидродинамические силы соответствующего клина, направленные по линиям Гутьяра mOi и feOa; Р - виещняя нагрузка, направленная по оси у.

Силы /1 и могут быть выражены в зависимости от соответствующих- относительных эксцентрицитетов xi = -y- и

/.2 = -f-, где S - радиальный зазор. Таким образом, в уравнениях (174) неизвестны четыре величины: Xi. Х2, 1. К Следовательно, для их определения необходимо иметь еще два уравнения. Из условия пересечения дуг подвижного равновесия, рассматривая треугольник OyOOi (фиг. 34), имеем

с = -f аз = = cos -f 2- (175)

Деля обе части равенства (175) на б и вводя

обозначение относительной толщины прокладки = -g- , получим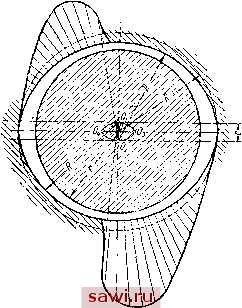

Фиг ,33. Положение цапфы в лимонном подшипнике.

C = Xi COS ai-f Х2 COS 2. Из того же треугольника ОООг имеем

sin а,

X2 = Xl

sin а,

(176)

(177)

Заметим, что 01 = 91 - а2=ф2 - &2-

Рассмотрим предельный случай устойчивости цапфы в смазочном слое по Ляпунову: нагружена лищь нижняя несущая

зона; давлений в верхней зоне еще нет, но они возникнут при малейшем отклонении центра цапфы от дуги подвижного равновесия. В этом Случае прямая Oitn приближается к вертикали, т. е.

1 - 0; 2 -

Так как

cos а; = cos (tpi - Sl) = cos <fi cos 9-1 + sin tpi sin Ь,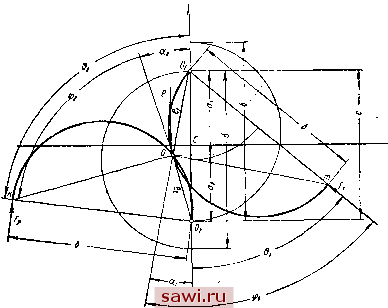

Фиг. 34. Определение положения центра цапфы в лимонном подшипнике методом отклоненных дуг подвижного равновесия.

ТО при & о получаем

cos а, = cos tpi + 9-, sin tpi. Из треугольника 0\0т имеем

COS<p,

sincp,=y 1 - Xi-

Следовательно,

cosai = Xi + iVl - tv

Далее

sin a, =sin(tpi ~ 9-]) = sin<Pi cos&i - cosi sinft,.