Выражения (213) -(215) представляют собой общий крите-)й устойчивости цапфы в многоклиновом подшипнике.

Для определения коэффициентов демпфирования рассмотрим 11 качестве конкретного применения критерия устойчивости че-: ырехклиновый подшипник, схематически представленный на фиг. 46.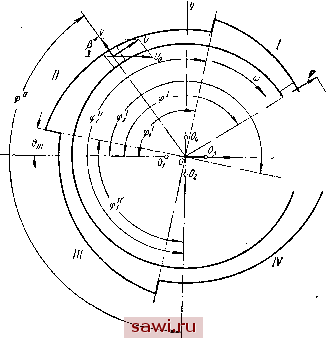

Фит. 46. Схема четырехклинового подшипника (к определению условия устойчивости).

При произвольном перемещении центра цапфы возникают демпфирующие силы в каждом клине. В силу симметрии подшипника достаточно найти коэффициенты демпфирования для двух соседних клиньев. Рассмотрим движение центра цапфы в первом квадранте, где расположен первый клин подшипника. Пусть начальное положение центра цапфы - точка О. Центры дуг каждого клина отмечены буквами О с соответствующими индексами.

Выберем систему координат так, чтобы ось х совпадала с линией центров 0]0, а ось у -с линией центров О2О. Компоненты силы демпфирования первого клина и соответствующие коэффи-

циенты демпфирования £j,. = -jj- определяются по обобщенному уравнению ейнольдса (48).

Так как клиновые выемки ограничены боковыми рантами, задерживающими торцовое истечение смазки, то можно принять скорость W = 0,

следовательно,- = 0.

Принимая р = const, = const и заменяя дх = гд, получим из уравнения (48)

l!?ri{h)=\2V + eiUh). . (216)

Здесь V - относительная скорость движения центра цапфы в радиальном направлении, U - b тангенциальном.

Если обозначить скорость перемещения центра цапфы вдоль

оси x буквой Uq, то. V-UoCOSqi и 6=(/о$1Пф.

Заметим, что величина 6 пренебрежимо мала по сравнению с другими членами уравнения (216); отбрасывая ее, получаем

lii-(/) = 12f/ cos,. .(217)

Заменяя h=r(\+/cos(fY v. интегрируя (217), имеем

отсюда

Введем условные обозначения интегралов

(1 -t-xcos ср)з~*з- . (221)

Определим постоянные интегрирования Cj и Сг учитывая граничные условия:

при <р = фз имеем р = 0; следовательно, С2 = 0; при <р = !р2 также р - 0,

откуда Ci = - ~-.

Следовательно,

f/- J (1 +XCoscp)3 ij (

(222)

f/- J (l+xcoscp)3 I J (l+xcoscp)3-

?i - 9i

Отсюда для силы демпфирования, возникающей в первом

клине, получим выражение

Q\.x- 1 fip cos 9й?9. Соответствующий коэффициент демпфирования

(223)

Обозначим Тогда

sin2 yrftp (1 -fx COS 9)3

sin2 tpdtp

sin tpdcp (1 -f X cos <p)3

(1 -f- xcostp)3

(224)

(225)

(226)

Аналогично для коэффициента демпфирования е получим

12хг

- Обозначим

sin tp cos cpdtp -fx cos cp)3

cos yrftp (1 +XCoscp)3

г sin tp cos tprftp

J (1 +xcos9)3-з;

С cos <prf<p

J (1+xcos9)3 -1-

(227)

(228)

(229) 157