Повышение температуры масла

д/! = ае.

В формулах (344) - (347) F - площадь поверхности одного сегмента; цо - вязкость масла на входе в подшипник; П, Н, I и 9 -безразмерные коэффициенты несущей силы, толщины слоя, сопротивления вращению и повышения температуры. Значения этих коэффициентов, вычисленные приближенным мето-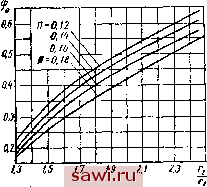

е.12

Фиг. 103. Оптимальные значения центрального угла ifo сегмента в за-

внсимости от отношения - и

без-

размерного коэффициента нагруженности Я.

Фиг. 104. Значение безразмерного коэффициента толщины смазочного слоя в зависимости от <f п П

при Ь6. 1

дом для оптимального отношения р = =1,6, приведены на фиг. 103-106.

Пример. Номинальная нагрузка на подпятник гидрогенератора Ро = 2000 /п; скорость вращения л = 83,3 об/мин; о}-=--= 8,72 рад/сек; смазка маслом турбинным 30, имеющим при 30° С вязкость р,зо = 6,8-10-3 /сГсе/с/л!; температура масла на входе принята 30° С; радиус Г] по конструкхиным соотношениям принят 1,075 м. Среднее удельное давление (принято предварительно) Рс = 50 кГ1см?. Коэффициент полноты х=0,7.

Решение. Обозначая отношение - =Р, имеем

Рс=-

Отсюда

2 106

14 1,0752 . 0,7 . 50 W

4- 1 = 1,6.

Так как Fz - !:r\{ - 1)х, то из формулы (344) следует

50 10*

= 0,13.

с-Ь ~ 0,41 427 .103-23

Здесь ст должно быть выражено в кГ/м. Для нефтяных масел су =0,41 ккал/дмград = 0,4\ 427 10 кГ/мград; д=23град. По фиг. 103 оптимальное значение центрального угла сегмента <ро = 0,375; число сегментов

27та 2 3,14 ,7 - 90 ~ 0,375

После округления z уточняются значения х = =0,716,

/)с = 52,6 10* кГм; Я = 0,135. По фиг. 104-106 этим значениям Я и <р соответствуют Я = 0,105; 7=1,43; 6 = 1,25. На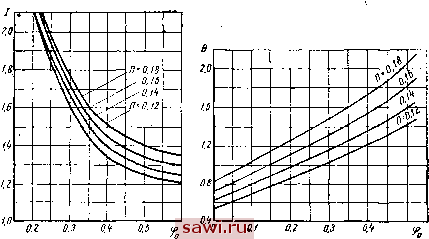

Фиг. 105. Значение безразмерного коэф- Фиг. 106. Значение безразмерного фициента сопротивления вращению / температурного коэффициента в в за-

в зависимости от 90 и Я при у= 1,6. висимости от 90 и Я при = 1,6.

основании формул (345) -(347) минимальная толщина масляного слоя / 1 = 61 10- ж = 61 мк; сопротивление вращению Mj-(o = 2,37 10* кГм/сек-.232 кет, повышение температуры Д = 29°С.

Решение уравнения Рейнольдса с учетом переменной вязкости в зависимости от температуры в различных точках смазочного слоя позволяет более точно определить основные параметры упорного подшипника. Расхождение в значениях несущей силы, определяемой обычным (при вязкости, принимаемой постоянной) и изложенным методом, когда (х = (х(/), достигает 10%] (при больших нагрузках и скорости). Однако и этот более точ-.

ный метод все же не свободен от ряда допущений и сопряжен с большой вычислительной работой, требующей применения счетно-решающих машин. Приведенные на фиг. 103-106 графики безразмерных коэффициентов относятся к частному случаю Р = -=1,6.Для других значений р необходимо снова выполнять всю серию вычислений и строить соответствующие кривые, чтобы найти оптимальные соотношения размеров сегментов для заданного режима работы. По-видимому, к таким расчетам целесообразно прибегать в тех случаях, когда уточнение порядка 5-10% играет существенную роль. В обычной расчетной практике упрощенный способ решения при fx = const (по средней температуре) дает в большинстве случаев достаточно точные результаты.

§ 34. РАСЧЕТ ПОДШИПНИКОВ С УЧЕТОМ УПРУГОЙ ДЕФОРМАЦИИ СЕГМЕНТА

При больших нагрузках, вызывающих существенную деформацию плоского сегмента, сопоставимую по порядку величины с минимальной толщиной смазочного слоя, следует вносить в расчет подпятника соответствующие коррективы. Под действием нормального давления и вследствие разности температур в отдельных точках сегмент деформируется так, что поверхность его можно принять с известным допущением близкой к сферической. В общем случае [64] расчет подпятников с уче- том упругой деформации сегментов основан на решении уравнений Рейнольдса и сохранения энергии (342) совместно с уравнением упругой деформации плоского сегмента

ЧЧ)=~ + ЦЧЧШ). (348)

Здесь = (1 + 7 -Tr + Ti-) -коэффициент Пуассона; s-толщина сегмента; а - коэффициент линейного расширения; модуль упругости материала сегмента.

Для облегчения совместного решения уравнений (342) и (348) приходится идти на некоторые упрощения: деформированную поверхность принимают за часть сферической поверхности с постоянным радиусом кривизны; тогда при v=0,3 прогиб в произвольной точке с координатами (л;, у) (фиг. 107)

радиус кривизны

Ро-2,23§-.