тивности. Последнее свойство зубчатого соединения обусловлено податливостью взаимодействующих элементов его деталей. По характеру взаимодействия их деформации могут быть нормальными и тангенциальными (за счет сил трения). Решающее значение для деформативности зубчатого соединения имеет нормальная жесткость его элементов, которую в дальнейшем будем называть просто жесткостью. В расчетах удобнее пользоваться величиной распределенной жесткости, которая представляет собой предел отношения приращения нормальной распределенной нагрузки к прираще-нию суммарного взаим- ного перемещения кон- тактирующих поверхностей в направлении действия нагрузки.

Согласно определению

dq(u)

(1.31)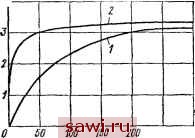

150q,HicH

Рис. 1.31. Зависимость жесткости от нагрузки для модели соединения из оргстекла: у - с ( ); 2 - гс ( )

где q (и) - распределенная нор.мальная нагрузка, Б общем случае зависящая от продольной координаты и\ (м) - взаимное перемещение поверхностей в направлении действия нагрузки, = = ti + 2 V\i Щ - перемещения зуба вала и зуба втулки.

Так как пару составляют зуб вала и зуб втулки, имеющие, как правило, разную податливость, жесткость пары определяется через жесткость составляющих ее элементов по известному соотношению

1/с =: 1/ci + llCi,

(1 32)

откуда следует, что с < Cj и с < Cj.

Необходимо отметить, что экспериментальные за.меры показывают, что при малых нагрузках распределенная жесткость пары зубьев не является постоянной. Кривйг 1 на рис. 1.31, полученная на модели зубчатого соединения из оргстекла 13 ], свидетельствует о том, что с увеличением

нагрузки жесткость возрастает и с некоторого значения нагрузки может считаться постоянной. Это явление, характерное для плоского стыка, связано с шероховатостью поверхности: фактическая поверхность контакта при малых нагрузках намного меньше геометрической и стремится к постоянной величине с ростом нагрузки.

Многочисленные эксперименты и расчеты, проведенные с учетом зависимости жесткости элементов соединения от нагрузки, позволяют сделать вывод о допустимости линеаризации расчетных зависимостей при решении задач о распределении нагрузки в соединении; иначе говоря, допущение с = const является вполне корректным.

Жесткость конкретного элемента соединения наиболее точно можно определить экспериментально. Поскольку при проектировании это не всегда возможно, обычно ее оценивают по геометрии соединения и упругим характерн стикам применяемых материалов. В общем случае вели чина взаимного перемещения пары зубьев может быть найдена как сумма перемещений, обусловленных изгибом зубьев Уц, поперечным сдвигом vx, контактной деформа цией Vk и перемещением за счет податливости основани (заделки) зуба. Однако большинство авторов (см. работы 1, 2, 22 и др.) не выделяют этих элементов, определяя взаимное перемещение пары зубьев по эмпирическим формулам вида

ю-Лд/Е, (1.33)

где Е - модуль упругости при растяжении.

Коэффициент 7, по данным В. С. Куликова [20], для ЭБОл вентных зубьев, с высотой головки, равной модулю равен 20-26,8; для стандартных эвольвентных зубьев с а - 30° и глубиной захода, равной модулю, по данным [2] равен 8-12. Э. Бакингем [42] для тех же ЭБОльве!:т ных зубьев (а = 30°, hs = т) упругое взаимное перемеик-ни зубьев принимает равным 0,001 дюйма при распреде ленной нагрузке 4000 фунтов на дюйм, что соответствует Я = 7,6. Для прямобочных зубьев % - 104-15. Связь между коэффициентом % и распределенной жесткостью пары зубьев с устанавливается соотношением

с = Efl. (1.34)

Жесткость зубьев эвольвентного профиля, данную по ГОСТ 6033-80, и прямобочного по ГОСТ 1139-80 можно

приближенно оценивать по формуле (1.34), а также по формулам, полученным Э. В. Рыжовым [29]; жесткость треугольных зубьев - по зависимостям, приведенным в [6].

Жесткость контакта цилиндрических центрирующих поверхностей Со (в случае, когда они контактируют) можно оценить по зависимостям, приведенным 3. М. Левиной и Д. Н. Решетовым [22].

Для наиболее распространенного случая, когда между центрирующими поверхностями имеется зазор, по сравнению с которым контактные деформации малы.

контакта не превышает одного-двух промежутков между смежными зубьями (при центрировании по d) или одной-двух толщин зуба (при центрировании по D). При этом условии распределенная (погонная) жесткость ющих поверхностей

Со = Vi.

Рис. 1.32. Зависимость коэффициента податливости от относительного натяга в гладком цилиндрическом соединении по данным работы [22]

В контакте центриру-

(1.35)

где bo - длина дуги контакта; kx - коэффициент контактной податливости для соединений с зазором. Значения находятся в пределах (0,2-ь0,3) 10 * см*/Н. Для случая, когда зазор между центрирующими поверхностями равен нулю, следует пользоваться зависимостью

(1.36)

где do - диаметр центрирования.

В случае применения для центрирования каких-либо вспомогательных цилиндрических или конических поверхностей (с малой конусностью, до 1 i 6) их жесткость определяется как жесткость гладкого цилиндрического соединения. Например, при использовании цилиндрических колец (см. рис. 1.6) шириной Ь, посаженных с натягом на вал и без зазора во втулку, жесткость центрирова-