ворота втулки \р, окружной силы на i-м зубе Л, и коэффициента неравномерности Ке, привеленные в табл. 3.2. В этих выражениях: == 0,5игсВг - нагрузочный фактор, а - угол исходного контура (для прямобочного профиля а = 0).

В формулах (I)-(III) рабочий угол О < вр < 0,5я определяется из условия Л = О, сводящегося к уравнению (IV). В формулах (1а)-(Ilia) Gp = 0,5л; они справедливы при Ni mm 0.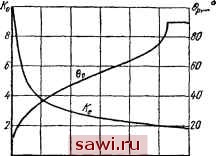

О OJL 0, 0.S OJB LOM/Mg

Рис. 3.6. Зависимость коэффициента окружной неравномерности Ке и рабочего угла вр от параметра MlMg

Из формул (III) и (II 1а, б, в) видно, что в стандартных соединениях с а = 30° неравномерность распределения нагрузки от овальности втулки немного выше, чем в прямобочных (tg а = 0,57735 > 0,5).

Зависимость бр и /f от безразмерного параметра М/Ме для прямобочного соединения, приведенные на рис. 3.6, аналогичны зависимостям Koiu) и КоЩШ/) (см. рис. 3.2). Это связано с тем, что основной составляющей ошибок шага А является разношаговость от овальности втулки.

Пример. Определить неравномерность распределения нагрузки в соединении 65X2,5X9H/9g (г = 24) длиной 55 мм, имеющем овальную втулку. Значение овальности 2u = 0,03 мм. Передаваемый момент М = 9500 Н-м.

Решение. Распределенная жесткость зубьев с = 0,2687-10? МПа, средний радиус соединения г= 3,125 см (см. пример в п. 3.1).

Таблица 3.2. Формулы дли расчета деформации соединения

и концентрации нагрузки

Условия применений

Расчетные формулы

афО; <2tga

М Г JX

X ( 1 + tgcx

sin 2ер

(2tga

L26p

cos 26,+sin 26,-

sin 26p

sin 26p

)tg

(П) (III)

sin 265 ~2§

tga-

- 2tgacos26p -sln26pj =0 (IV)

a=fO;

l+-f-(l + tgcx)] (la)

1 + (2 tg a cos 26,+sin 26,)

(Ila)

if,= I + 2-tga (Ilia)

a = 0;

M Me

(1116)

K,= l +

(IIlB)

a = 0; <l

/ sin2ep \

Нагрузочный фактор Же = O.SuzcBr = 0,5.15.10-6.24.0,2687- lOMOe .5,5 10 ?.3,125. IQ-z = = 7980 Н-м.

Безразмерный параметр нагрузки

-~ = -- = 1.1904 > 2 tg а = 2 tg 30° = 1,1547,

следовательно, нагружены все зубья. Коэффициент окружной неравномерности определится по формуле (Ilia) из табл. 3.2.

3.3. Окружная неравномерность распределения нагрузки,

вызванная поперечной силой

Поперечной силой для соединений зубчатых колес является нормальное усилие в зацеплении, для соединений шкивов ременных передач - суммарное натяжение ветвей ремня, для соединений звездочек цепных передач - окружное усилие и т. д. Во всех случаях поперечная сила остается неподвижной, следовательно, нагрузка, приложенная к соединению, имеет циркуляционный характер. После приработки соединения (происходящей довольно быстро - за 2-3 % срока службы) окружная неравномерность связана только с действием поперечной силы.

В общем случае поперечная сила уравновешивается геометрической суммой окружных сил на зубьях втулки и реакцией центрирующей поверхности, а момент окружной силы - суммой моментов окружных сил. Отсюда следует, что нагрузку, передаваемую t-й парой зубьев, можно найти, решив г - 1 раз статически неопределимую задачу о равновесии втулки [6, 12, 15, 22]. Если считать, что вал и втулка под действием нагрузки не меняют своей формы (круглые поверхности остаются круглыми), условия равновесия без учета сил трения можно записать в виде (см. схему на рис. 3.7);

yNiCOsei-}-No-P = 0; NiSinQiO; fNir -

-Рго = 0,

где Nt - окружная сила, приложенная к t-му зубу 6/ - координатный угол, отсчитываемый от плоскости