этой парой нагрузки распределение последней будет соответствовать схемам, представленным на рис. 3.12.

При начальном контакте (рис. 3.12, с) угол относительного поворота в соединении определяется зазором Aj т. е. \ро = AbID; при небольшой нагрузке (рис. 3.12, б, в) эпюра ее имеет форму треугольника с основанием, меньшим глубины захода, а угол относительного поворота 1)5 ilo + Дь/. а при > Дь(1/£> + 1/d) эпюра принимает трапецеидальную форму (рис. 3.12, г).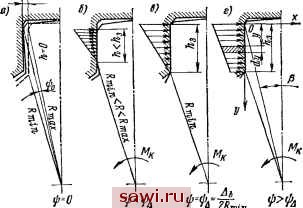

Рис. 3.12. Характер распределения нагрузки по глубине еахода в зависимости от уровня передаваемой нагрузки

Среднее напряжение смятия согласно схемам, представленным на рис. 3.12, определится так;

(0,5D - y)it>

cos Р

- 0Mb dy.

(3.22)

где К - коэффициент податливости в контакте.

Пренебрегая изменением угла Р по глубине захода, можем принять

cos p J/D2-bVD.

Максимальное напряжение смятия I

( -0,5Аь).

(3.23)

Коэффициент неравномерности распределения нагрузки /Сй является отношением максимального напряжения к среднему. При гр Дь (Z> + d)/(Dd)

=--mrwHs- (3.24

Из формулы (3.24) следует, что Кн с уменьшением At, стремится к величине

Kb = D/(D-h,). (3.25)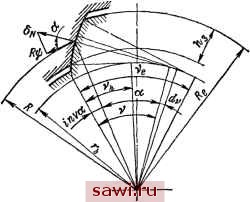

Рис. 3.13. Нормальное перемещение элемента рабочей поверхности эвольвентного вуба

Для эвольвентных зубьев нормальное перемещение элемента поверхности, определяемое радиусом R (рис. 3.13),

6л, == R/cos а \rt (v -f 1), (3.26)

где Гь - радиус основной окружности соединения; v - угол развернутости эвольвенты, соответствующий радиусу R.

Среднее напряжение смятия на длине контакта /д, соответствующей глубине захода /ig,

3 = 0.5r,(v-v), (3.27)

где = е -f- inv а, - угол развернутости эвольвенты, соответствующий окружности выступов вала; =

= aft + inv ttft - угол развернутости, соответствующий окружности выступов втулки, определяется по формуле

Оср = 7 11Гt (v + 1) - 0,5Дь] V dv. (3.28)

Подставив /з и выполнив интегрирование, получим

Максимальное напряжение смятия ama. = 4-b(v=+!) (. (3.30)

Из (3.28)-(3.30) следует, что при загрузке зуба на полную глубину захода

. = -ЖгЧг- (3.31)

Таким образом, концентрация нагрузки по глубине захода эвольвентного соединения зависит только от его геометрических параметров и бокового зазора.

Для треугольных зубьев величину Кн можно принимать равной коэффициенту неравномерности для эвольвентных зубьев, т. е. определять его по формуле (3.31); при этом угол исходного контура а следует считать равным углу профиля треугольных зубьев.

3.6. Крутильная и поперечная жесткость плоского зубчатого соединения

Крутильной жесткостью зубчатого соединения считают предел отношения приращения крутящего момента AM к приращению относительного поворота вала и втулки Ачр

Поперечной жесткостью считают предел отношения приращения поперечной силы АР к приращению поперечного относительного перемещения втулки и вала Ау в направлении силы

c,= lim = 4. (3.33)

Крутильная и поперечная жесткость соединения зависят от его размеров, жесткости его элементов, точности