в (4.4) и (4.4а) параметры Я, и р определяются формулами:

(4.5)

(4.6)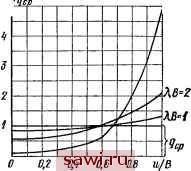

402 р2

Отнеся максимальную нагрузку niax = q (В) к средней, получим коэффициент продольной неравномерности распределения нагрузки при

снятии момента со сто- ------1-\~~iS=S роны под вода

= KB/th KB; (4.7)

при снятии момента со стороны, противоположной подводу,

-ch W]]

ЯД{1-(рА)М1-

~ thXB

~sh%B. (4.7а)

На рис. 4.2 приведена зависимость отношения q{u) к средней нагрузке ср в зависимости от безразмерного параметра ХВ. С ростом этого параметра неравномерность распределения нагрузки увеличивается.

При сочетании продольной неравномерности с окружной (например, от разнозазорности) в формулы (4.5) и (4.6) следует подставлять условное число зубьев

гр = 20р/р = г0р/я

(здесь р - угловой шаг).

4.2. Влияние формы ступицы на продольную неравномерность распределения нагрузки

в зубчатых соединениях

В подавляющем большинстве случаев вал, сплошной или полый, имеет цилиндрическую форму, следовательно, для него Jpi = const. Ступицы же далеко не всегда, как

Рис. 4.2. Зависимость продольного распределения нагрузки от параметров жесткости (безразмерной величины ХВ)

видно из рис. 4.3, имеют столь простую конструкцию. Когда

Gi/p,( )<0.1G,/p.( ). (4.8)

уравнение совместности и выражения для Kip упрощаются, так как угол закручивания ступицы становится пренебрежимо малым. Неравенство (4.8) будет выполнено, когда при равных упругих характеристиках материалов наруж-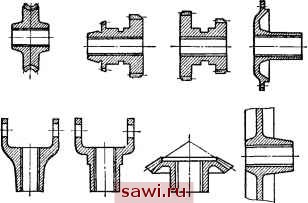

Рис. 4.3. Конструктивные типы ступиц вубчатых соединений

ный диаметр ступицы £)ст и средний диаметр соединения rfcp находятся в соотношении

1.8d,

(4.9)

Большинство конструктивных исполнений зубчатых колес, шкивов, полумуфт и других деталей не укладывается в пределы неравенства (4.9). Например, по нормам ЭНИМСа для зубчатых колес коробок передач станков DJd = 1,5-7-1,7, нормы DIN рекомендуют это отношение брать 1,6 для стальной и 1,8 для чугунной ступицы. В. Н. Кудрявцев рекомендует значение этого отношения, равное 1,5. В конструкциях ступиц деталей транспортных машин (шестерни коробок передач, карданные вилки, фланцы, соединяющие полуоси с диском, и т. д.) это отношение не превосходит 1,3, опускаясь в отдельных случаях до 1,12-1,15.

Для учета фактического влияния формы ступицы необходима квадратура уравнений (4.3)-(4.3а) с учетом вида функции Jp {и). При этом распределенная жесткость с (q) может быть принята постоянной и не зависящей от нагрузки.

Интегрирование уравнения совместности даже при простейшей конической форме ступицы затруднительно.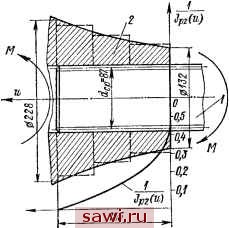

Рис. 4.4. Конусообразная ступица

Однако можно показать, что применение конусообразных ступиц (рис. 4.4) может способствовать выравниванию продольного распределения интенсивности нагрузки. Действительно, так как

ТО при

9( ) = <7ср = з = const

Ml (u) = М{В - u)lB, М[ (и) = 0. и из (4.3а) следует, что

G2p2( ) = £3n7iV

(4.10) 143