(4.4); в противном случае параметр X определяется по (4.5) при /р2 = сю, т. е. (GJpz) = 0. При этом

q (и) и du

chlB-l

(4.23)

q(u)du

В общем случае изгибающий момент воспринимается реактивным моментом соединения с моментами на торцах ступицы М, если имеет место торцовая затяжка

= + М. (4.24)

Статическая неопределимость (4.24) может быть раскрыта условием совместности деформаций, т. е. угол перекоса у должен быть равен углу поворота торцов -ут. которые должны быть перпендикулярны к оси соединения и затянуты хотя бы до отсутствия зазора

V = Yt. (4.25)

Однако практика показывает, что в результате трения между торцами ступицы, нагруженной поперечной силой, и торцами соседних деталей осевая затяжка рано или поздно падает до нуля, и изгибающий момент передается только соединением. Это дает основание считать = О независимо от того, предусмотрена осевая затяжка или нет.

Поскольку нагрузка к соединениям щестерен, щкивов и звездочек цепных передач приложена циркуляционно, неравномерность ее распределения и поперечную силу, вызываемые разнозазорностью, можно не учитывать.

Условия равновесия втулки зубчатого соединения (рис. 1.8, 3.7) имеют вид (без учета сил трения);

Ni SinGi = 0;

(4.26)

Система (4.26) является замкнутой с разделяющимися переменньмн, т. е. распадается на две системы; первые три уравнения решены в п. 3.3, последние два представляют собой Z - 1 раз статически неопределимую систему. В формуле (4.26) Mi - реактивный момент t-й пары зубьев соединения относительно оси хх, Myi - то же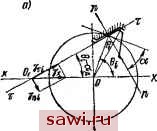

S) 1

Рис. 4.9. Геометрия перекоса: a - эвольвентного и треугольного соединений; б - прямобочного соединения; в - распределение нагрузки вдоль -го зуба

относительно оси уу; Мо - реактивный момент центрирующей поверхности относительно оси хх; остальные обозначения - те же, что в п. 3.3.

Для раскрытия статической неопределимости воспользуемся уравнениями совместности деформаций, которые получим, рассмотрев геометрию перекоса соединений, рис. 4.9: в результате перекоса поворот t-й пары происходит вокруг касательной к плоскости контакта, следовательно.

V = cos Gj - для прямобочных зубьев;

V* == Y*cos(e,- - а)-для эвольвентных зубьев.

(4.27) 151

в зависимости от соотношения угла перекоса yi, поперечной у и угловой ф деформаций соединения теоретически возможны следующие случаи:

1) все зубья соединения нагружены на полной длине;

2) часть зубьев нагружена не по всей длине;

3) часть зубьев не нагружена совсем;

4) нагружены нерабочие стороны зубьев.

Как показывает опыт эксплуатации, последний случай практически не встречается.

Если считать применимой гипотезу Винклера и пренебречь краевыми эффектами, эпюра распределения нагрузки для первого случая имеет форму трапеции, на наименее нагруженном и наиболее перекошенном зубе она может выродиться в треугольник эпюры (типа 1 ч 2, рис. 4.9, е). Для второго и третьего случая эпюра распределения нагрузки для некоторых зубьев имеет форму треугольника с основанием, большим В/2 {В - длина соединения) или меньшим В/2 (эпюры соответственно типа 3 и 4).

Чтобы получить несложное аналитическое выражение для реактивного момента соединения, общее для трех первых рассматриваемых случаев, придется принять следующие допущения.

1. Будем считать, что реактивный момент имеют только те зубья, на которых эпюра распределения нагрузки имеет вид 1, 2 или 3 (рис. 4.9, е), иными словами, будем учитывать реактивный момент только трех пар зубьев, которые передавали бы нагрузку при равной поперечной деформации и отсутствии перекоса.

2. Реактивный момент зубьев, на которых эпюра распределения нагрузки имеет вид 5, будем считать равным реактивному моменту зубьев, распределение нагрузки на которых соответствует виду эпюр 1 к 2.

3. Реактивный момент центрирующих поверхностей будем учитывать только в случае, если поперечная деформация соединения превышает половину зазора между центрирующими поверхностями, иначе говоря, только в том случае, если на центрирующей поверхности при равной поперечной деформации и отсутствии перекоса появляется реакция.

4. Реактивный момент центрирующих поверхностей будем определять исходя из треугольной эпюры с основанием, равным длине соединения. При этих допущениях