Подставляя (5.13) и (5.14) в (5.12), получаем трансцендентное уравнение для определения Bi

2 L л J

являющееся справедливым при

М[М],щ1Ъ1В. (5.16)

где Ш ]т - момент, соответствующий началу пластических деформаций рабочих поверхностей зубьев.

Пластические деформации в галтели зуба начнутся при условии достижения в какой-либо точке главным нормальным напряжением а, касательным к контуру переходной кривой, предела текучести.

Напряжение наиболее просто определяется по известной гипотезе ломаных сечений проф. А. В. Верхов-ского [25] либо по формуле Хейвуда [38], полученной на основании анализа диаграмм фотоупругости. При использовании метода А. В. Верховского значение крутящего момента, соответствующего началу текучести в точке А на контуре переходной кривой (рис. 5.8), определяется по зависимости

2 (Ко + Я - 1) Н - )

где Ко, Кп - общие коэффициенты окружной и продольной неравномерности; х - расстояние в системе координат XOY от точки пересечения линии действия нагрузки q с осью симметрии зуба до вершины ломаного сечения; у - ордината, соответствующая полуширине обычного плоского сечения; а - угол давления, равный углу профиля зуба; а - угол между направлением главного нормального напряжения, касательного к контуру зуба в точках Ai, и осью симметрии зуба; Н - безразмерный коэффициент, зависящий от положения ломаного сечения и определяемый по выражению

тг 0,5 COS п. (f\\R\

3j p + 2cosocn (cos n + ? p)2 cosoc; 2( рЯ (у/рг cosccn + tj/p

где р - радиус кривизны выкружки зуба,

При использовании метода Хейвуда крутящий момент, соответствующий началу текучести, определяется по выражению

2 (Ко -Ь Кп - 1) [1 - 0,26 (e/i?) -! 5а , 0,45 , sinP \-i

где параметры а, Ь, е, R, р приведены на рис. 5.9.

(5.19)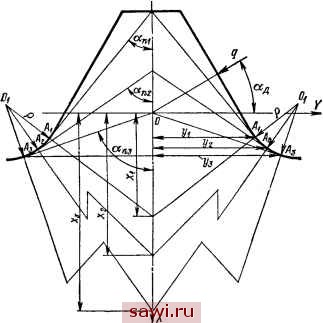

Рис. 5.8. Расположение ломаных сечений при изгибе треугольного зуба

Для сравнения указанных методов в табл. 5,3 приведены данные по определению максимального напряжения в точках начала, середины и конца выкружки эвольвентных зубьев валов, имеющих z == 34 зуба при Ко => = Кп = 1- Из приведенных данных следует, что метод Хейвуда дает значения напряжений примерно на 15-

Таблица 5.3. Значения местных напряжений в зубьях эвольвентного профиля (по ГОСТ 6033-80) при действии распределенной нагрузки в 10 Н/см