25 % большие, чем максимальные значения напряжений по Верховскому.

Пластические деформации в теле зуба могут появиться в том случае, когда максимальное периферийное нормальное напряжение для прямобочного зуба или приведенное (по 3-й или 4-й теории прочности) для треугольного (эвольвентного) зуба достигнет предела текучести. При определении касательных напряжений т, входящих в выражение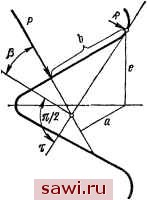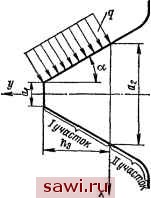

Рис. 5.9. К определению максимального местного напряжения по Хейвуду

Рис. 5.10. Схема вагрузки зуба треугольного профиля

Приведенного напряжения, необходимо учитывать граничные условия и определять т из первого уравнения плоской задачи теории упругости.

Для треугольного симметричного профиля, загруженного равномерно распределенной нагрузкой в пределах глубины захода (рис. 5.10) выражения для напряжений будут различными для участка /, где действует нагрузка, и для участка , свободного от нагрузки.

Для участка /

о =

й (я.-f 2л tga)3 h3(ai-i-2A;tga)*

3 qx (txi + X tg

2 h3(ai-t-2A:tgaf

(5.20)

(6.21)

для участка

12 (дх + О.бйз) У . /с оо.

=--(a, + 2;.tg )3 ( ==

6?yMa2-4;ctga- Shatga) 3 (ag -atga) /г pov Из уравнения

Ко1. + 4т=а, (5.24)

при фиксированных у находим значения х, при которых начнется текучесть.

Абсциссы точек, ограничивающих выход зоны текучести на кромку профиля (при вершине зуба вала), для участка /

2gitga -/ 4gf tgg i; .p. p.v

где Л = 4 tg a - 3kil/l +4: tg a ; 9/(Лз т) - относительная загруженность профиля.

Из (5.25) следует, что текучесть на участке / возможна, когда

fe> ie; (5.26)

при а = 30° ki > 0,29; при меньших значениях относительной загрузки текучести не будет. Кроме того, ограничением возможного появления текучести является условие

X < к (5.27)

Для участка из аналогичных соображений находим,

ifeiS>-, ° (5.28)

Максимальные касательные напряжения, возникающие у внутренней поверхности ступицы с зубьями эвольвентного или треугольного профиля,

где pb - условное давление по цилиндрической поверхности ступицы диаметром Df,

рьд sin a/inDf), (5.30)

D - наружный диаметр ступицы.

Так как текучесть наступит, когда Тп,ах = 0,58ат, то нагрузка, вызывающая пластические деформации во впадинах отверстия,

0.29d,peBD,(Dg pna.

так как окружная неравномерность при определении условного давления по Ламэ не учитывается.

При массивной втулке (D -> оо) зависимость (5.31) упрощается

= (5.32)

Пример. Для соединения с треугольным профилем, выполненного из стали марки 45ХНМФА с пределом текучести 1080 МПа, длиной В = 4,8 см при dcp = 6,525 см, z = 52, с углом профили 30°, глубиной захода Ьз - 1,75 мм, толщиной d, = 0,7 мм, da = 2,7 мм (см. рис. 5.4), радиусом закругления выкружки зуба р = 0,075 см, параметром Я = 0,676 см , определить предельные значения крутящих моментов по смятию рабочих поверхностей и появлению текучести в месте концентрации напряжений и в теле зуба.

Решение. Предельное значение крутящего момента по смятию рабочих поверхностей зуба определяется по формуле (5.16)

.Ml 1080-10 -0,175.10-2.52-6,525-Ю- , =-2-0.676.102-0.676-4,8 =

= 4,75.1fr МПа.

Для определения момента, соответствующего началу текучести в выкружке зуба, проводятся три ломаных сечения через точки А±, Ai, (см. рис. 5.8). Значения координат х, у, угла давления an, полученные непосредственно из чертежа, и значения вычисленных параметров, входящих в формулу (5.17), сведены в табл. 5.4. Из данных таблиш следует, что появления текучести следует ожидать в точке А, Из формулы (5.17) для точки А при Ко= Кп- 1 получаем

1080-10 -4,8-10-2-6,525-10-2-52 cos 30° 1МЬ =-27rW\-= 98- 0 Н--

Согласно критерию (5.26) текучесть на участке / зуба (рис. Ъ.Щ становится возможной, когда ? = 0.29/!зат = 0,29-0,175-1080 = == 5520 Н/см, что соответствует крутящему моменту

5520 cos 30° 6,525-52-4,8 3д,д, Н-м. 194