наты и. Граничные условия должны учитывать схему подвода и снятия момента.

Исходная система из семи уравнений путем последовательного дифференцирования сводится к однородному дифференциальному уравнению кручения седьмого порядка с постоянными коэффициентами:

МГ (и) 4- А,М {и) 4- ЛгМ! (и) + АгМ[ (ы) = 0. (6.1)

где коэффициенты Ai, А, А зависят от параметров жесткости GiJpi, GJpi, GaJpa, GJpt, Ci, c, Cp размеров r.

Анализ результатов, полученных на ЭВМ, подтверждает предположение [23], что при крутильных жестко-стях колес, хотя бы на порядок больших, чем крутильные жесткости валов, функции qi (и) и q (и) можно считать параметрически зависящими только от GJp и GgJps. Это положение снижает статическую неопределимость задачи до единицы и позволяет определить нагрузку в зацеплении из решения неоднородного дифференциального уравнения второго порядка

dpiu) /1 , \ , ч ,

- (+-g;j) р +

+ CSra V + 0 ch Ки = о, (6.2)

где параметры жесткости А, К определяются по формуле (4.5), i = 21/22, 2i, Z2 - число зубьев соединений 1 и 2.

Граничные условия для уравнения (6.1) определяются из уравнения совместности деформаций шестерни и колеса в зацеплении, приводящегося к виду

Mi {и) j . Ms (и) ! 2j

GiJp2 G3J j,3 .

Из формулы (6.3) и граничных условий для моментных функций следует: р (0) = 0; р (В) = 0.

Для иллюстрации зависимости распределения нагрузки вдоль зубчатого венца р (и) от жесткости зубчатого соединения на рис. 6.2 представлены кривые р (и), построенные для ZC = 0,1 Ср и ZC = Юср. При малой жесткости соединения функция р (и) сходна с функциями q (и) и Ml (и), при большой - с функцией М2 (и), имеющей максимум. Неравномерность распределения нагрузки в зацеплении, оцениваемая отношением pmaJPcp> умень-

шается с 1,17 до 1,05 при переходе от жестких зубьев соединения к более податливым. В том и другом случае неравномерность оказывается ниже, чем определяемая по данным [5, 18, 19, 41 ], а также ниже, чем для вала-шестерни.

Перекос ступицы относительно вала под действием изгибающего момента поперечной силы приводит к продольной неравномерности распределения нагрузки в зацеплении. По мере износа соединения этот перекос дол-

..у... .л-

4.6 4.3

3.7 3,4

0 3 6 9 11 Ю 21 U.CH

Рис. 6.2. Зависимость распределения нагрузки по длине зацепления в зависимости от жесткости зубчатых соединений

жен возрастать до тех пор, пока не наступит равновесие ступицы в результате смещения нормальной силы в зацеплении (рис. 6.3). Исследования, проведенные под руководством Г. И. Скундина (31, 32], показывают, что если продольная асимметрия зубчатого колеса не превосходит определенного предела, износ соединения после непродолжительного периода приработки становится равномерным по длине. Это возможно при одном условии - Мх = О, а это означает, что нормальная сила в зацеплении и равнодействующая системы реакций в соединении находятся в одной плоскости. При этом угол перекоса ступицы Ух возрастает по сравнению с первоначальным, для неприработанного по длине соединения, а перекашивающий момент падает до нуля. Эпюра нагрузки в зубчатом зацеплении из прямоугольной преображается в трапецеидальную (рис. 6.3, а) или треугольную с основа-

нием, равным длине контакта b (рис. 6.3, б), или мень-шим ее. Если зубчатые колеса не прирабатываются, то для первого случая (рис. 6.3, а) Мх == О при

й + Ь- с>Ь/3; (6.4)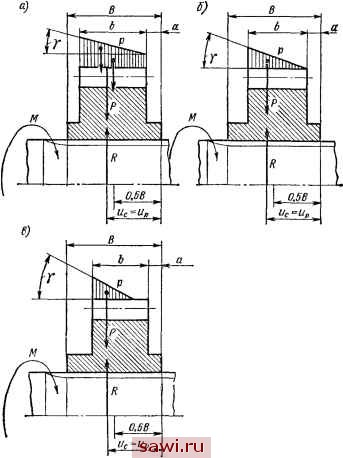

Рис. 6.3. К определению установившегося угла перекоса шестерни

установившийся угол перекоса при этом Y,= I2-( -b/2-fi),

где Ср - распределенная жесткость зацепления. 200

(6.5)