Таким образом, условие, что объем является одно-связным, выполняется, если любая замкнутая кривая внутри этого объема может быть рассмотрена в качестве контура плоской площади, расположенной целиком внутри объема. Если принять это определение, то объем, заключенный между двумя концентрическими сферами, является односвязным.

Рис. 10

Рис. 11

28. Многосвязный объем имеет тело, в котором имеется одно или несколько отверстий: количество отверстий обозначает порядок кратности. Таким объемом может быть тор (рис. 11).

В многосвязных объемах можно провести замкнутые кривые двух родов. Кривые первого рода, подобные тем, что были определены в предыдущем параграфе, могут быть деформированы в точку, не покидая объема. В торе они будут окружностями, проведенными в меридианной плоскости, концентрическими с одной из меридианных окружностей.

Кривые второго рода, которые не могут быть превращены непрерывной деформацией в точку, не покидая объем: например, на торе - это окружности, проведенные в плоскостях, перпендикулярных оси и имеющие свои центры на этой оси.

29. Предположим теперь, что вихрь всюду равен нулю

С = 77 = С = О,

J = J {и dx -\- V dy -\- W dz).

Этот интеграл, взятый вдоль замкнутой кривой первого рода равен нулю. Действительно, согласно п. 9, имеем

J = I 2rbdu;,

где является нормальной компонентой вихря, а du; - элементом площади, ограниченной кривой. Согласно предположению,

= о, имеем J = 0.

Это предположение справедливо и для кривых второго рода. Действительно, предположим, что объем является тором и что

и= v= J w = {).

х + 2/ + у

Линии тока являются окружностями, имеющими центры на оси и проведенные в плоскостях, перпендикулярных этой оси. При этом

ydx - xdy , у udx + vdy =---- = 6?arctg -.

Функция скоростей arctg не является однозначной, но имеет бесконечное множество значений, различающихся на тг. Когда будем брать интеграл J вдоль кривой второго рода, этот интеграл не будет равен нулю, а равен тг или кратен ему, потому что, возвращаясь в начальную точку, мы приходим к другому значению этой функции.

30. Разрезы. Когда объем является многосвязным, его возможно представить в односвязном виде, для чего необходимо проделать некоторое количество разрезов. В частности, если объем является дву-связным, достаточно проделать всего один разрез. Например, тор может быть представлен в односвязном виде, если разрезать его вдоль одной из меридианных окружностей.

Кривые, которые не пересекают разрез, будут представлять собой кривые первого рода; кривые, пересекающие разрез, - второго рода.

Функция скоростей остается однозначной пока не пересекает разрез, а интеграл J, взятый вдоль кривой, не пересекающей разрез, равен нулю.

и рассмотрим интеграл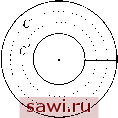

С другой стороны, рассмотрим две бесконечно близкие друг другу и разрезу точки, но расположенные по разные стороны от этого разреза. Функция скорости испытывает разрыв между двумя точками; разность величин, которые она принимает в двух этих точках будет конечной и равной интегралу J, взятому вдоль кривой второго рода, соединяющей эти две точки.

31. Теорема. Эта разность постоянна, другими словами, значение интеграла J одинаково для всех кривых интегрирования, которые пересекают разрез только один раз.

Действительно, предположим, что кривая С деформируется непрерывным образом, не покидая объем и, например, отклонясь в сторону как С (рис. 12). Во время этой деформации кривая С заметает некоторую площадь, которая полностью расположена внутри объема.

Интеграл J, взятый вдоль полного контура этой площади СС, равен нулю.

Однако две кривые С и С пробегаются при интегрировании в противоположных направлениях так, что

Jc -Jc=0

Значение разрыва функции скоростей на границе разреза постоянно во всех точках и равно А.

Если кривая второго рода после интегрирования дважды пересекает разрез, то разрыв функции if будет 2А и так далее. Вообще, если контур интегрирования пересекает разрез п раз в направлении по часовой стрелке и п раз в направлении против часовой стрелки, значение интеграла будет равно (п - п)А.

32. Если объем трехсвязный (рис. 13), то, чтобы представить его в односвязном виде, необходимо проделать два разреза. Тогда функция

скоростей if является вполне определенной, но она имеет разрыв на границе каждого из разрезов. Разрыв имеет одну постоянную величину А

Рис. 12

Рис. 13