Установка Видеонаблюдения, Охранной и Пожарной сигнализации.
Звоните! Приедем быстро! Установим качественно! + гарантия 5 лет.
| Тел. ОАО «Охрана Прогресс» Установка Видеонаблюдения, Охранной и Пожарной сигнализации. Звоните! Приедем быстро! Установим качественно! + гарантия 5 лет. |
||
|
Установка технических средств охраны. Тел. . Звоните! Главная Влияние вязкости жидкостей 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 Таким образом, эта скорость обратно пропорциональна расстоянию MN = р, как и было найдено выше другим способом. 49. Прямое доказательство. Для того чтобы получить выражение функции ip, нет необходимости сравнивать уравнения гидродинамики и электродинамики между собой, что было проделано нами выше. Как было доказано, это выражение может быть получено непосредственно. Для простоты будем говорить, что функция ip порождена контуром с, когда она обусловлена вихревой трубкой, осью которой является контур с, а момент принимается равным единице. Выбор единицы, очевидно, ничего не меняет в большинстве наших доказательств. Приведем сначала несколько теорем, которые будут необходимы для получения выражения функции ip. 50. Теорема I. Рассмотрим замкнутую кривую ABCD (рис. 16). Соединим две точки В, D этой кривой некоторым путем BED. Таким образом образуются два частичных контура ABED, BCDE и один полный контур ABCD. Допустим, что эти контуры образуют оси трех вихревых трубок Т,Т и Т. Каждый из контуров порождает функцию ip. Пусть ip, ip и ip - функции соответствующие Т, Т и Т, соответственно. Тогда ip = ip + ip . Выберем в качестве контура интегрирования окружность, описанную в плоскости, перпендикулярной прямой PQ, с радиусом MN и центром в точке N. Примем PQ за ось z, точку N - за начало координат и два диаметра окружности, перпендикулярные друг относительно друга, - за оси х w у.В этой системе отсчета х = рсоио, у = psinuj, dx =-psinuj duj, dy = p cos со duj, dz = 0, u = -Vsinuj, v = Vcosuj, a; = 0. Откуда, /i = у pV{sm uj + cos uj)duj = 27грУ, У = Действительно, через три кривые можно провести некоторую поверхность, определяющую два разреза. Функция (р допускает существование двух разрезов; при этом ср допускает только разрез (1), а ср - только (2). Для того чтобы вывести теорему, достаточно показать, что тождественно имеем ср-ср -ср = 0. Эта функция удовлетворяет уравнению Лапласа - - = О, Рис. 16 так как Аср = Аср = Аср = 0. Она равняется нулю в бесконечности так же, как и частичные функции (р, (р, ip . Это позволяет применить к функции теорему Грина п. 34, если она является однозначной, то есть если интеграл J dip- J dip - J dip = 0 вдоль некоторого замкнутого контура. Предположим, что кривая интегрирования будет кривой первого вида, то есть не будет пересекать никакой разрез, тогда три частичных интеграла равны нулю. Если кривая пересекает только разрез (1), то f dip равен моменту трубки Т, т.е., согласно гипотезе, единице, f dip равен моменту трубки Т, т. е. также единице. / dip равен нулю. Уравнение снова выполняется. Это можно было бы установить тем же способом, при условии, что кривая интегрирования пересекает только разрез (2). Некоторый замкнутый контур всегда может быть заменен рядом контуров, каждый из которых пересекает только один разрез (рис. 17). 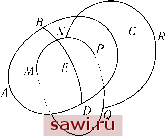 Рис. 17 Равенство момента трубки единице следует из того, что момент трубки постоянен вдоль контура, а на отрезке BAD моменты трубок Т и Т равны. - Прим. ред. Поэтому контур MNPQ, пересекающий два разреза, может быть заменен на MNRQM, который пересекает только первый разрез и NPQRN, который пересекает только второй разрез. Действительно, эти два контура меняют направление для того, чтобы обойти начальный контур в определенном направлении, а дуга NRQ побегает один раз в одном направлении и один раз в противоположном и в результате исчезает. Следовательно, вдоль некоторого контура J dip- J dip - J dip = 0.  Функция ip-ip-ip является однозначной и, следовательно, по теореме Грина, тождественно равна нулю. 51. Теорема II. Функция ip, порожденная плоским контуром С, равняется нулю в любой точке плоскости. Пусть С - контур (рис. 18). Обозначим направление вихря стрелкой и рассмотрим отражение относительно плоскости контура. Функция ip при этом не должна изменяться. Точка М, принадлежащая плоскости симметрии, не изменяется; момент трубки сохраняет то же абсолютное значение, но меняет знак. Рис. 18 так как движение вихря меняет направление. Функ- ция ip в точке М в одно и то же время не должна изменяться и должна поменять знак. Следовательно, она может быть равна только нулю. 52. Теорема 111.Предположим, что контур С прочерчен на поверхности конуса, имеющего вершину в точке М (рис. 19). Можно прочертить на поверхности конуса два вида кривых: первые, ограничивающие площадь, в которой вершина отсутствует-, другие, производящие оборот вокруг конуса и ограничивающие площадь, которая включает в себя вершину. а. Для кривых первого вида функция ip равна нулю в точке М. Действительно, можно разложить С на бесконечно малые контуры, каждый из которых может быть отождествлен с плоским элементом, находящимся в плоскости, касательной к конусу: так как все эти касательные плоскости проходят через вершину конуса М, то функция ip, порожденная каждой из них, равна нулю. Функция ip, порожденная полным 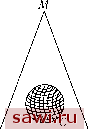 Рис. 19 Установим охранное оборудование. Тел. . Звоните! |