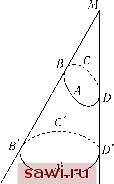Рис. 20

контуром С, являющимся суммой элементарных функций п. 50, будет также равна нулю.

Ь. Пусть теперь существуют две кривые второго вида ABCD и ABCD (рис. 20). Тогда функции if, порожденные этими двумя кривыми, имеют одинаковое значение в точке М.

Действительно, соединим, например, образующей ВВ точку В первой кривой с точкой В второй кривой; соединим таким же образом DD. Затем заменим контур ABCD на контуры ABCD, ABBADDC, CDDCBBC. Описывая последовательно эти три контура в направлении, указанном последовательностью букв, обойдем каждую из дуг, за исключением ABCD, два раза в противоположных направлениях. Функции if, порожденные двумя последними контурами, равны нулю согласно первой части теоремы (а). Таким образом, функции, порожденные кривыми ABCD и ABCD, имеют одинаковое значение в вершине конуса.

53. Бесконечно малый контур. Вид функции if. Пусть контур бесконечно мал. Функция if, а priori, может зависеть от расстояния г между точкой М и элементарной поверхностью, ограниченной контуром; от угла ф между прямой, соединяющей точку М с центром тяжести элемента, и вектором площади элемента поверхности; от площади этого элемента и, наконец, от его вида. Другими словами, может зависеть от г, от ф, от телесного угла и от формы конуса с точкой М в качестве вершины и контуром в качестве направляющей.

Сначала покажем, что if не может зависеть от формы конуса. Действительно, рассматриваемая бесконечно малая площадь первого порядка может быть разложена на квадраты, которые будут бесконечно малыми второго порядка. Все квадраты имеют одинаковую форму, а угол ф имеет одинаковое значение для каждого из них с точностью до бесконечно малых высшего порядка. Кроме того, какова бы ни была форма рассматриваемой площади, количество квадратов можно сделать таким, чтобы их совокупность отличалась от исходной площади как

угодно мало. Значением ер, образованной полным контуром, будет сумма функций ер каждого из квадратов. Эти функции будут одинаковы для каждого квадрата, поскольку г и -0 одинаковы и квадраты имеют одинаковую форму. Таким образом, полная функция ер будет пропорциональна числу квадратов, то есть площади, ограниченной контуром, и не будет зависеть от его формы. Следовательно, установим следующее соотношение

ер = f{r, ф)(1(7,

где da - телесный угол конуса и / - функция, которую необходимо определить.

Телесный угол da имеет одно и то же значение вдоль конуса; с другой стороны, две замкнутые кривые С и С , проведенные на конусе, должны порождать одинаковые функции ер; однако для этих двух кривых гиф могут быть любыми. Таким образом, необходимо, чтобы выполнялось равенство

/(г, ф) = const = А.

54. Рассмотрим конечную замкнутую кривую. Разложим ее на элементарные кривые, для каждой из которых ер пропорциональна телесному углу da. Для их совокупности получим соотношение

ер = Аа,

где а - полный телесный угол.

Для того чтобы определить А, предположим, что точка М описывает некоторый замкнутый контур, откуда следует, что

J dep = А J da,

если назовем р моментом вихревой трубки, то

dep = р.

С другой стороны, справедливо равенство

da = 47Г,

4:7Ги =

dy dz

dadl dj dx dy dz

в случае, когда жидкость заполняет односвязный сосуд, необходимо, чтобы нормальная к поверхности составляющая скорости равнялась нулю в любой точке этой поверхности. Если обозначить через /, ш, п направляющие косинусы нормали, то это условие запишется следующим образом

1и -\- mv -\- nw = 0.

Для получения соответствующей электродинамической задачи необходимо предположить, что токи преобладают внутри поверхности стенки S, а все внешнее пространство занимает сверхпроводник. Если, начиная от состояния покоя, постепенно увеличивать внутренние токи, то во внешнем пространстве появятся токи индукции. После установления процесса электродвижущая сила индукции исчезнет, однако токи индукции останутся, поскольку внешняя среда является сверхпроводником (т.е. ее сопротивление равно нулю). В данной постановке электродинамическая задача совпадает с задачей Гельмгольца.

откуда

fjL = 47гА

55. Жидкость, полностью заполняющая односвязный сосуд. Мы ставим себе целью определить и, v, w по следующим уравнениям

ос - dw dv ~ ду dz

ди dv dw q dx dy dz

которые в электродинамике соответствуют уравнениям

dj d/3