Вне цилиндра имеем равенство

х = Хо, У = Уо, z = 2:0; во внутренней части -

x = Xo-\-vt, у = УО, z = Zq.

Таким образом, х является разрывной функцией от xq, уо, zq.

Если ж, у, z являются непрерывными функциями от xq, уо, zq, то частицы жидкости, образующие в начальный момент времени t = О кривую или непрерывную поверхность, образуют новую кривую или непрерывную поверхность в некоторый момент времени f; если же кривая в начальный момент времени замкнута, то она остается таковой в любой момент времени t.

Действительно, пусть частицы в начальном положении образуют некоторую кривую. Уравнения этой кривой могут быть выражены следующим образом:

хо = /о( ), Уо = /о( ), 0 = /Л )

где /о, /о, /о являются непрерывными функциями параметра а.

Во время t координаты частиц становятся ж, у, z, они же в свою очередь, согласно гипотезе, являются непрерывными функциями от xq, 2/0, Zq. Следовательно, они будут непрерывными функциями и от а:

x = f{a), у = Г{а), z = r{a).

Эти уравнения определяют также непрерывную кривую.

Если первоначальная кривая Со замкнута, то xq, уо, zq являются периодическими функциями от а. Так как х, у, z - однозначные функции жо, Уо, Zq, они также будут периодическими функциями от а, а кривая С, заполненная частицами в момент времени также является замкнутой.

Если частицы в начальный момент времени занимают непрерывную поверхность So, то их координаты выражаются следующим образом

Хо = /о( , /3), Уо = /о( , /3), zo = fo{a, где /о, /о, /о являются непрерывными функциями от параметров (а, jS). В момент времени t координаты становятся х, у, z w будут непрерывными функциями от жо, Уо, Zo и, следовательно, от (а, (3). Таким образом:

ж = /( ,/?), y = f(a,f3), z = f {a,f3),

где /, / - непрерывные функции; и эти уравнения задают непрерывную поверхность S.

3. Уравнение непрерывности. Рассмотрим элемент поверхности duj и попытаемся оценить количество жидкости, которое пересекает этот элемент в течение времени dt. Частицы, пересекающие элемент duj за время f, переходят в момент времени t - dt в элемент поверхности duj бесконечно близкий duj. В частности, центр тяжести G элемента duj переходит в G - центр тяжести элемента duj. Частицы, которые пересекают duj за время t + dt заполнят сам этот элемент. Наконец, те частицы, которые пересекли duj в интервале между t Ht-\-dt будут находиться в промежуточных положениях.

Подводя итог сказанному, отметим, что все частицы, которые прошли через duo за время dt находятся в момент t -\- dt в объеме, уподобляемом цилиндру, имеющему основание в виде элемента duo, с образующими параллельными GG (рис. 1). Заметим также, что GG = V dt, где V является скоростью жидкости в рассматриваемый момент времени. Высота цилиндра является проекцией GG на нормаль к duj. Таким образом: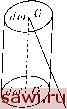

Рис. 1

Рис. 2

Vdtco8{GGN) = Vndt,

а количество жидкости, пересекающей элемент duo за время dt, равно:

pVn duo dt.

Рассмотрим теперь прямоугольный параллелепипед, ребра которого параллельны осям координат и соответственно равны dx, dy, dz (рис. 2). Из ранее сказанного следует, что масса жидкости, которая пересекает за время dt сторону ABCD, перпендикулярную оси Ох, равна:

ри dy dz dt,

а масса жидкости, которая пересекает противоположную сторону:

С другой стороны, приращение массы жидкости pdxdydz в объеме параллелепипеда за время dt будет иметь вид

- dx dy dz dt,

так как dt представляет приращение плотности р за время dt. Таким образом, необходимо, чтобы

др д{ри) д{ру) d{pw) dt дх ду dz

что представляет собой уравнение непрерывности в системе переменных Эйлера. Это уравнение может быть записано также следующим образом:

либо, принимая во внимание отношение (2),

Отметим, что в последней форме содержится два вида производных.

4. Упрощение уравнений Лагранжа. Уравнения Лагранжа поддаются упрощению, если принять некоторые допущения, необходимые для применения принципа Гельмгольца.

Если силы X, Y, Z допускают потенциал V, имеем:

дх ду dz

Таким образом, масса жидкости, вошедшей в параллелепипед через эти стороны, выражается в виде

- dx dy dz dt. дх

Производя подобные вычисления для двух других пар сторон, можно найти, что общая масса жидкости, вошедшей в параллелепипед за время dt, равна:

(д{ри) d{pv) d{pw)